一、python中的字符串(str)
1、python中字符串的存储形式

2、str构造操作的实现
O(1)时间操作:求串长、定位访问字符(python中没有字符类型,这里的访问的是只包含一个字符的字符串)
O(n)时间操作:需要扫描整个串的内容例如:in、not in、min、max、判断字符串类型
二、字符串匹配
1、朴素的串匹配算法

步骤:在初始状态两个串的起始字符对齐(i,j = 0,0)。将模式串和目标串进行逐个字符顺序比较,直到模式串中的某个元素和目标串中不一样则将模式串右移一位(i,j = 0, j - i + 1)继续顺序比较,直到找到完整个目标串长度即可。
def naive_matching(t,p):
m,n = len(p),len(t)
i,j = 0,0
while i < m and j < n: # i == m 说明找到了匹配
if p[i] == t[j]: #字符串相同考虑下一对字符
i,j = i + 1, j + 1
else: # 字符不同,则考虑t中的下一个位置
i,j = 0,j - i + 1 # 此处在计算j时使用的是更新前的i值
if i == m:
b = j - i
print(b)
return j - i # 无匹配返回特殊值
return -1
if __name__ == '__main__':
s1 = '0000001'
s2 = '001'
naive_matching(s1,s2)
朴素的串匹配算法比较简单,容易理解,但是效率低。算法复杂度为O(mxn)。m为模式串长度,n为目标串长度。
2、无回溯串匹配算法(KMP算法)
2.1 KMP简述
朴素串匹配算法没有利用字符串本身的特点,每次移位都是从头比较,没有在算法执行的过程中记录信息。KMP算法的精髓就是开发了一套分析和记录模式串信息的机制(和算法),而后借助得到的信息加速匹配。
2.2 构建pnext表(关键)
KMP算法关键是生成一个next表,在表中会记录在对应的模式串中的位置 i 与目标串的位置 j 匹配失败后,模式串下一步应该跳的位置。如果模式串在 j 处的字符跟目标串在 i 处的字符匹配失败后,下一步用next[ j ] 处的字符继续跟目标串 i 处的字符匹配,相当于模式串向右移动了 j - next[ j ] 位。
构造pnext表,分为两步:(1)求模式串中各子串的前后缀公共元素的最大长度值;(2)pnext表相当于最大前后缀整体向右移动一位,然后初值赋 -1。
首先解释下为什么要找前后缀的最大值,请看下图:

目标串中的位置 j 之前的 i 个字符也就是模式串中的前 i 个字符,也就是说,目标串中的子串 t(j-i) ......t(j-1)就是p(0)......p(i-1)。现在需要找到一个位置 k ,下次匹配用pk与前面匹配失败的 tj 比较,也就是把模式串移动到 pk 与 tj 对准的位置,如图如果移动的正确,模式串中的子串 p(0)......p(k-1) 就应该与子串 p(i-k)......p(i-1) 匹配,而这两个子串分别为串 p(0)......p(i-1) 的长度为 k 前缀和后缀。这样,确定k的问题就变成了确定p(0)......p(i-1)的相等的前缀和后缀的长度。显然,k 值越小表示移动的越远。另一方面为了保证不遗漏可能的匹配,移动的距离应该尽可能的短,所以应该找的 k 是p(0)......p(i-1)的最长相等的前缀和后缀(不包括p(0)......p(i-1)本身,但可以是空串)的长度,这样才能保证不会跳过可能的匹配。
下面举例说明 pnext 表的构建
假设给定的模式串为“ABCDABD”,从左至右遍历整个模式串,其各个子串的前缀后缀分别如下表格所示:
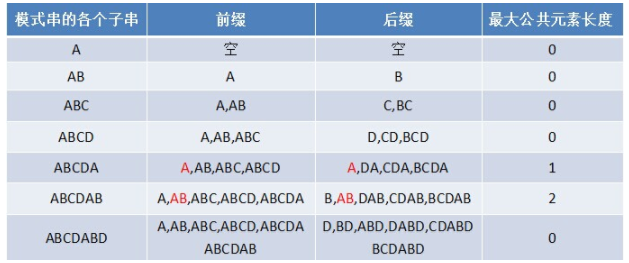
从而有
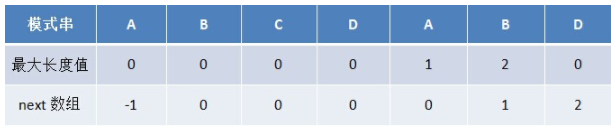
所以失配时,模式串向右移动的位数为 : 失配字符所在位置 - 失配字符对应的pnext值
2.3 代码递推pnext值
如下图所示,假设现在要对子串p(0)......p(i-1) p( i )(也就是对位置 i)递推计算最长相等前后缀的长度,这时对 pnext [ i - 1] 已经计算出结果为 k - 1,比较 p(i) 与 p(k),有两种情况:
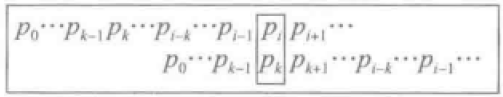
(1)如果 p(i) = p (k),那么对于 i 的最长相等前后缀的长度,比对 i - 1 的最长相等前后缀的长度多 1 ,由此应该pnext[ i ] 设置为 k ,然后考虑下一个字符。
(2)否则就应该把 p(0)......p(k-1)的最长相等前缀移过来继续检查。
注意,第二种情况并没有设置,只是继续检查。
已知pnext[ 0 ] = -1 和直至 pnext[ i - 1] 的已有值,求pnext[ i ]的算法:
(1)假设pnext[ i - 1] = k - 1,如果p(i)= p(k),则pnext[ i ] = k,将 i 加 1 后继续递推(循环)。
(2)如果 p(i)!= p(k),就将 k 设置为 pnext[ k ] 的值(将 k 设置为 pnext[ k ],也就是转区考虑前一个更短的保证匹配的前缀,可以基于它继续检查)。
(3)如果 k = -1,(这个值一定是由于第2步而来自pnext),那么p(0)......p(i)的最长相等前后缀的长度就是0,设置pnext[ i ] = 0,将 i 值加 1 后继续递推。
程序如下 gen_pnext(p) 为pnext表构建程序,matching_KMP(t,p,pnext) 为 KMP算法整体程序。
def gen_pnext(p):
#生成针对p中各位置i的下一个检查位置表,用于KMP算法,已知pnext[0]=-1和pnext[i-1]直至的已有值求的算法,为了创造这样的条件,故在开始时设置所有的初始值为-1
i,k,m = 0, -1, len(p)
pnext = [-1] * m # 初始数组元素全为-1
while i < m - 1 : # 生成下一个pnext元素值
if k == -1 or p[i] == p[k]:
i,k = i + 1,k + 1
pnext[i] = k # 设置pnext元素
else:
k = pnext[k] # 退到更短相同前缀
print(pnext)
return pnext
def matching_KMP(t,p,pnext):
'''
KMP 串匹配,主函数
:param t: 目标串
:param p: 模式串
:param pnext: next 表
:return:
'''
j,i = 0,0
n,m = len(t),len(p)
while j < n and i < m: # i==m说明找到了匹配
if i == -1 or t[j] == p[i]: #考虑p中的下一个字符
j,i = j + 1,i +1
else: #失败!,考虑pnext决定的下一个字符
i = pnext[i]
if i == m:
print(j - i)
return j - i # 找到匹配返回其下标
return -1 # 无匹配返回特殊值
if __name__ == '__main__':
#gen_pnext("abbcabcaabbcaa")
matching_KMP("zzzabbcabcaabbcaa","abbcabcaabbcaa",gen_pnext("abbcabcaabbcaa"))
2.3 KMP算法的复杂度
一次KMP算法的完整执行包括构造pnext表和实际匹配,设模式串和目标串长度分别为m和n,KMP算法的时间复杂度为O(m + n),由于 m << n,因此该算法的时间复杂度为O(n)。