ID3算法:
ID3算法就是在决策树上各个结点应用信息增益准则作为特征筛选,然后递归的构建决策树。具体算法如下所示:
输入:训练数据集D,特征集A,阈值e
输出:决策树T
(1)若D中所有实例属于同一类Ck,则T为单结点树,并将Ck作为该结点的类标记,返回T
(2)若A为空,则T为单结点树,并将D中实例最大的类Ck作为该结点的类标记,返回T
(3)否则,计算A中各特征对D的信息增益,选择信息增益最大的特征Ag
(4)如果Ag的信息增益小于阈值,则T为单结点树,并将D中实例数最大的类Ck作为该结点的类标记,返回T
(5)否则,对Ag的每一个可能值ai,按照Ag=ai将D划分为多个非空子集Di,将Di中实例数最大的类作为标记,构建子结点,由结点及其子结点构成树T,返回T
(6)对第i个子结点,以Di为训练集,以A-Ag作为特征集,递归调用(1)-(5),得到子树T1,返回T1
该算法的缺点在于:
1)倾向于选择取值较多的属性,而这类属性很多情况下没法提供太多价值。
2)只能为选择属性为离散性的变量构造决策树
C4.5算法(与ID3的差别在于C4.5以信息增益比作为特征筛选):
输入:训练数据集D,特征集A,阈值e;
输出:决策树T
(1)如果D中所有实例属于同一类Ck,则将T作为单结点树,并将Ck作为该结点的类,返回T
(2)如果A为空,则将T作为单结点树,并将D中实例数最大的类Ck作为该结点的类,返回T
(3)否则计算A中各个特征对D的信息增益比,选择信息增益比最大的特征Ag
(4)如果Ag的信息增益比小于阈值,则将T作为单结点树,并将Di中实例数最大的类Ck作为该结点的类,返回T
(5)否则对于Ag的每个可能取值ai,按照Ag=ai将D划分为若干个子集Di,将Di中实例最大的类作为标记,构建子结点,由结点及其子结点构成树T,返回T
(6)对结点i,以Di为训练集,以A-{Ag}为特征集,递归调用(1)-(5),得到子树Ti,返回Ti
注:信息增益比公式
![]()
优点:
1)该算法克服了ID3算法偏向于取值较多的属性的缺点。
2)可以处理连续数值型属性(对连续型数据从大到小排序,生成n-1个分割点,选取信息增益率最大的点作为分割点)
3)采用后剪枝方法
4)缺失值处理
缺点:构造树过程需要对数据集扫描和排序,导致算法低效。
决策树的损失函数有如下表达式:
![]()
其中经验熵表示为:
![]()
以上的|T|表示树T的叶结点个数,t是树T的叶结点,该叶结点有Nt个样本点,其中k类的样本点有Ntk个,k=1,2,...,K,Ht(T)为叶结点t上的经验熵,
该损失函数的第一项可以表示为:
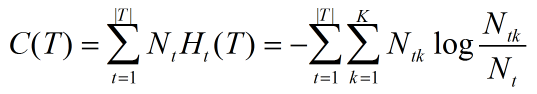
因此原损失函数可以简化为:
Ca(T)=C(T)+a|T|
上式中C(T)表示模型对训练数据的误差,|T|表示模型拟合程度。
剪枝算法的思路主要在于:剪枝之后的Ca(T)能达到更小的水平
决策树的剪枝:
预剪枝:
即设定阈值,若在增加新的分割时,熵减少的数量小于这个阈值,则停止创建分支
后剪枝:
通过对具有同一个父结点的结点判断,判断在结点合并之后熵的增加值是否小于阈值,如果小于该阈值,则这对子结点可合并为一个结点,并将原父结点作为新的叶结点。
REP(错误率降低剪枝):
通过将子树转为叶结点,以子树中最多的类作为该叶结点类,以单独测试集来比较转换前后是否错误率有所提高,若有所提高则删除子树,无则往上遍历。
PEP(悲观剪枝):
(待补充)