范数介绍:https://www.zhihu.com/question/20473040?utm_campaign=rss&utm_medium=rss&utm_source=rss&utm_content=title
首先介绍损失函数,它是用来估量你模型的预测值f(x)与真实值Y的不一致程度
主要的几种类型包括:1)0-1损失函数 2)平方损失函数 3)绝对损失函数 4) 对数损失函数
0-1损失函数:
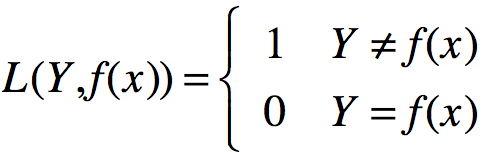
平方损失函数:
![]()
绝对损失函数:
![]()
对数损失函数:
![]()
由此延伸出对应的概念:

其次介绍一般的范数表示:
范数包括向量范数和矩阵范数,向量范数表征向量空间中向量的大小,矩阵范数表征矩阵引起变化的大小。一种非严密的解释就是,对应向量范数,向量空间中的向量都是有大小的,这个大小如何度量,就是用范数来度量的,不同的范数都可以来度量这个大小
向量的范数:
1-范数,计算方式为向量所有元素的绝对值之和。

2-范数,计算方式跟欧式距离的方式一致。
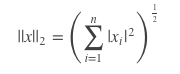
矩阵的范数:
假设矩阵的大小为m∗n,即m行n列。
1-范数,又名列和范数。顾名思义,即矩阵列向量中绝对值之和的最大值。
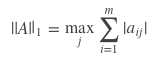
2-范数,又名谱范数,计算方法为ATA矩阵的最大特征值的开平方。
正则化也就是经验风险项加上正则化项,从而达到对模型选择的目的,以做到从模型拟合效果(经验风险)和复杂度(正则化项)来选去最优模型。
正则化的一般表示形式为:

其中第一项表示经验风险,第二项表示正则化项
正则化可以表示为多个形式,以回归方程为例,由于其损失函数为平方损失,正则化表示为参数向量的L2范数:
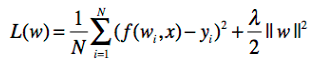
在这里||w||表示参数向量w的L2范数。
正则化也可以表示为参数向量的L1范数
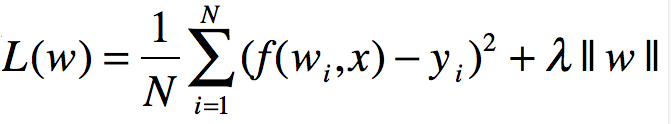
其中||w||表示参数向量w的L1范数
以上部分的经验风险表现越小模型越复杂,这时候正则化项为表现较大,所以我们主要还是筛选经验风险和正则化项同时较小的模型。
注:
L1范数因为表现出比L0范数更好的求解性而应用较为广泛
L2范数表现为向量各元素平方和求平方根,我们让L2范数的正则项||W||2最小,可以使得W的每个元素都很小,都接近于0。