引入:
抛硬币1:
有A,B,C三枚硬币,我们想要估计A,B,C三枚硬币抛出正面的概率πA,θB,θC。我们按如下流程进行实验100次:
随机抛一次硬币A
若硬币A抛出正面,则抛10次硬币B
若硬币A抛出反面,则抛10次硬币C
记录100次实验的结果如下:


抛硬币2:
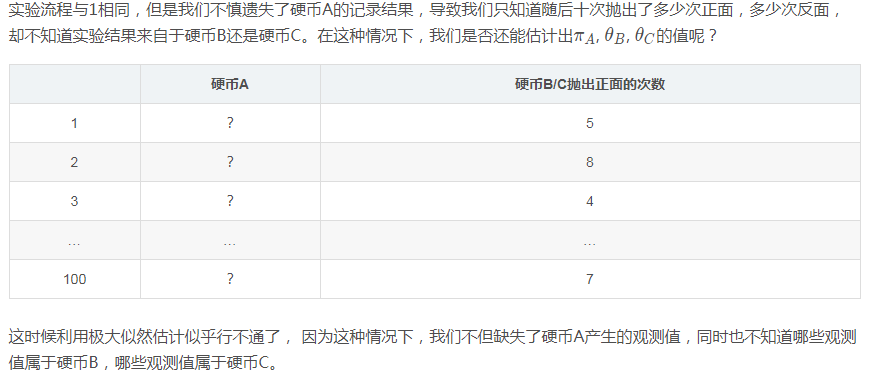
有些同学可能会提出,虽然我们无法得到三个硬币各自产生的样本,但是我们依然可以得到每个观测值出现的概率。比如在第一次实验中, 我们抛出了5次正面5次反面,我们可以做如下思考:


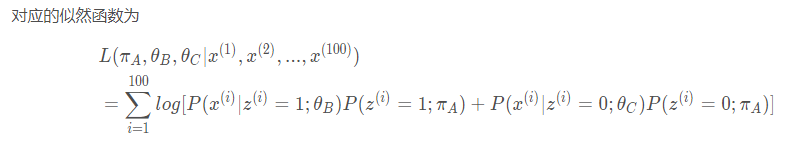
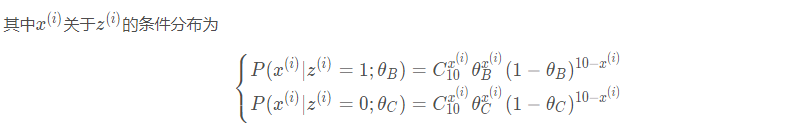
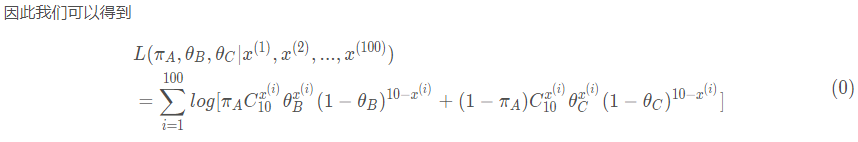
至此,我们成功地得到了似然函数。然而观察可以发现,这个函数是由100项对数函数相加组成,每个对数函数内部包含一个求和,想通过求导并解出导数的零点几乎是不可能的。当然我们可以通过梯度下降来极小化这个函数,借助深度学习库的自动微分系统在实现上也非常容易。但是这种做法过于简单粗暴,有没有办法来优雅地解决这个问题呢?在继续讨论之前,我们先将这类问题进行一般化表述:
ES算法的数学原理:















E-step和M-step
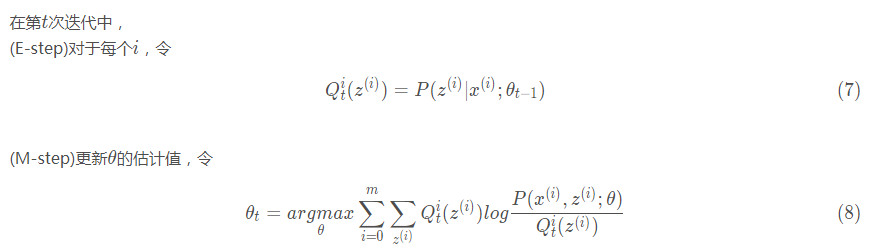



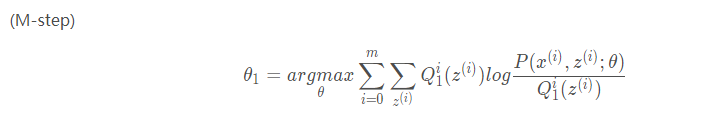







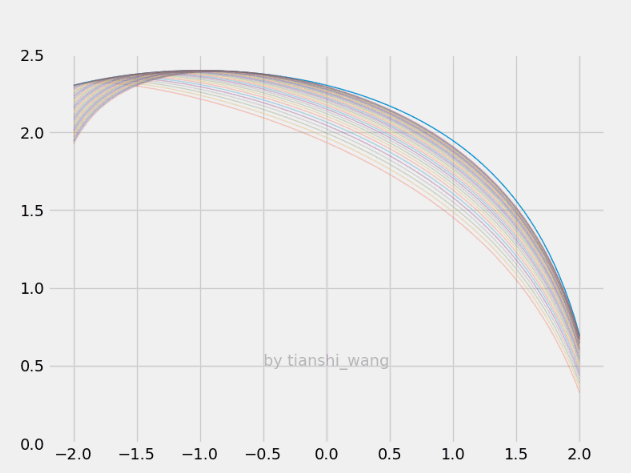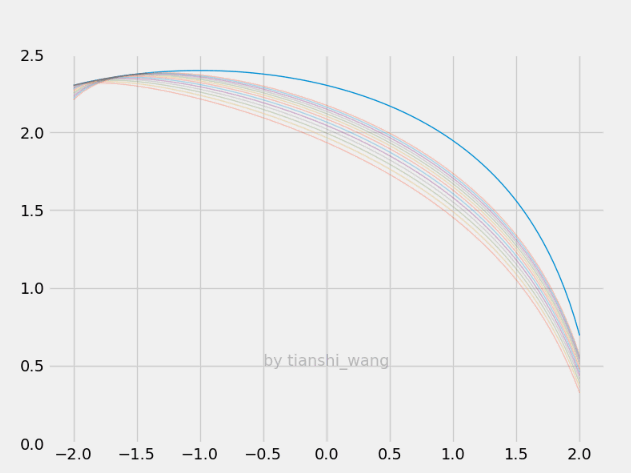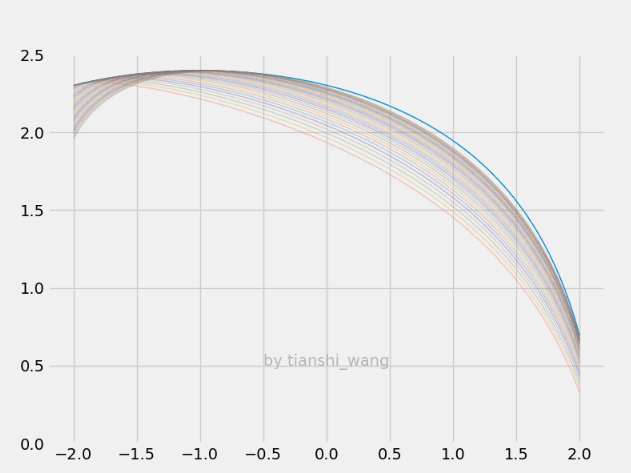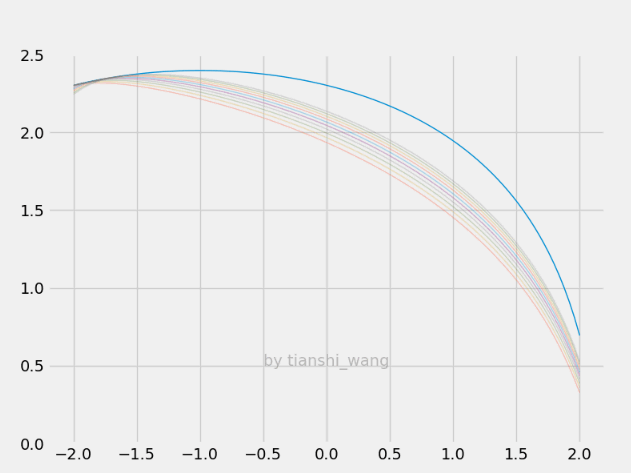

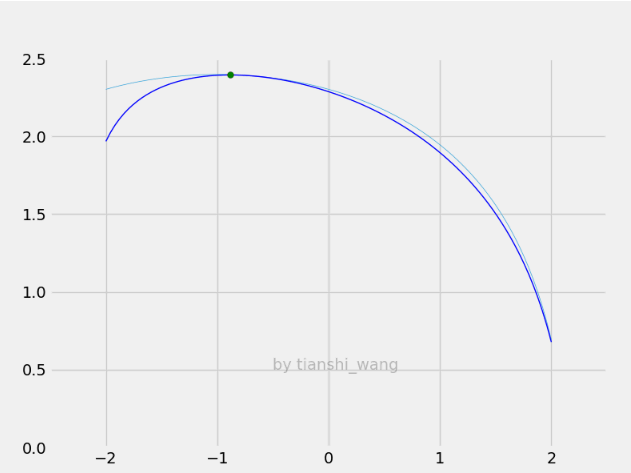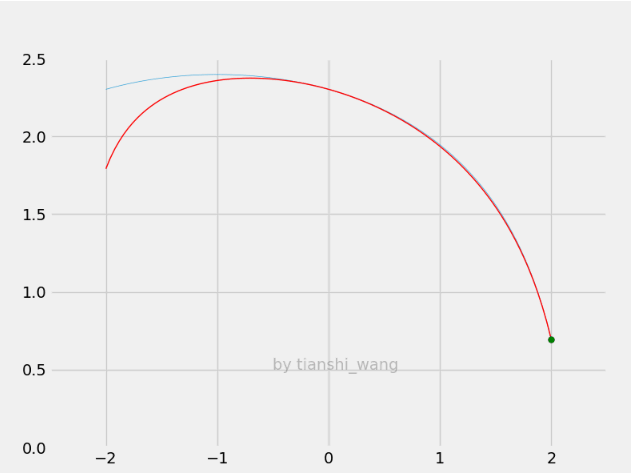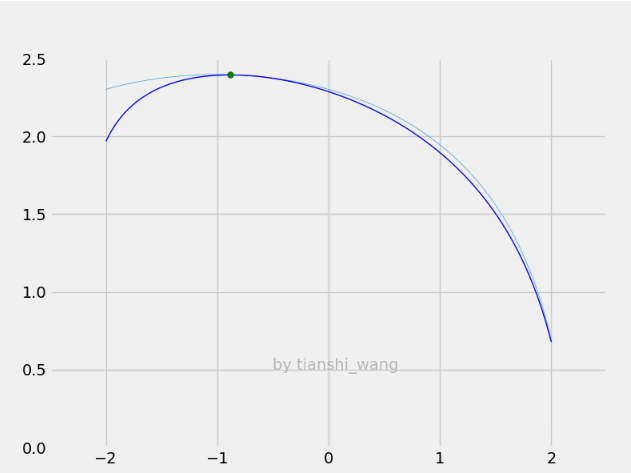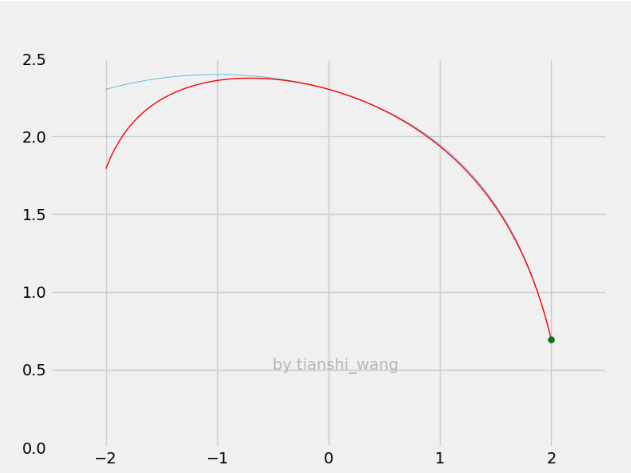


=====================================================================================
转载自:https://blog.csdn.net/weixin_43661031/article/details/91358990?utm_source=qq&utm_medium=social&utm_oi=75236821172224