大厂算法面试之leetcode精讲24.其他类型题
视频讲解(高效学习):点击学习
目录:
65. 有效数字 (hard)
图是网络结构的抽象模型,是一组由边连接的节点
图可以辨识任何二元关系 比如路、航班
图的表示方法
- 邻接矩阵
- 邻接表
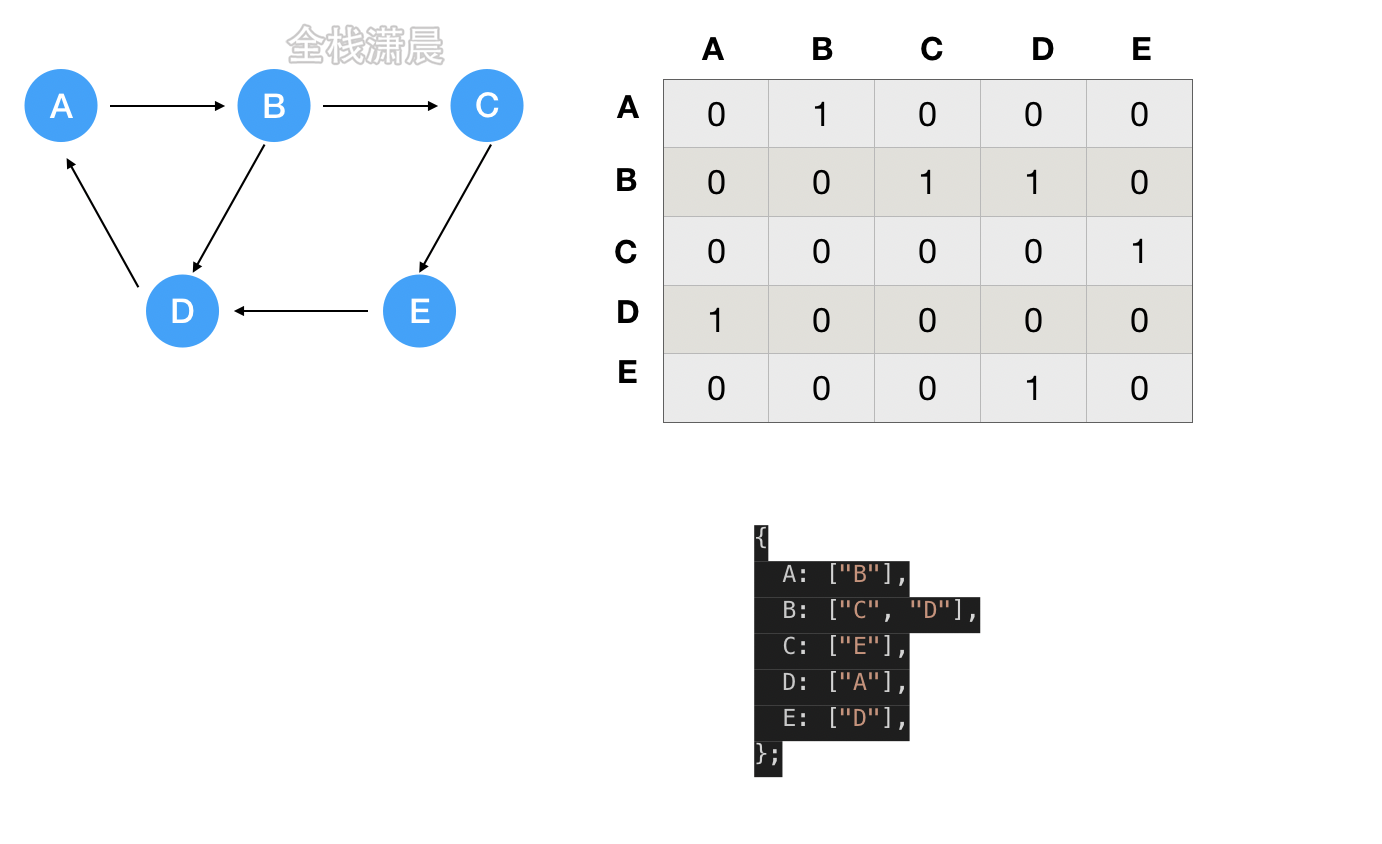
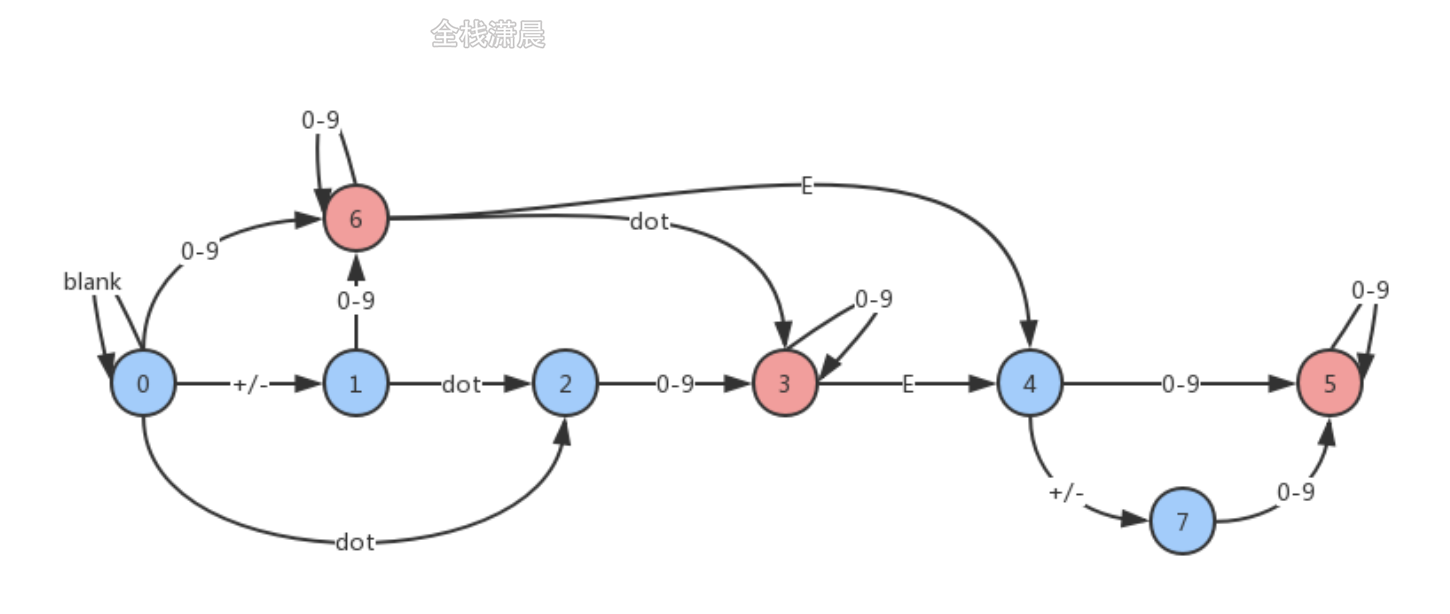
- 思路:有限状态机,遍历字符串,不断转换状态,看最后的状态是是否是有效状态
- 复杂度:时间复杂度
O(n),n是字符串的长度,遍历n次,每次状态转移是O(1)。空间复杂度O(1)
js:
//1.2 2e10
//--6 2e
var isNumber = function(s) {
const graph = {//点和边构成的临接表
0:{ 'blank': 0, 'sign': 1, '.': 2, 'digit': 6 },
1:{ 'digit': 6, '.': 2 },
2:{ 'digit': 3 },
3:{ 'digit': 3, 'e': 4 },
4:{ 'digit': 5, 'sign': 7 },
5:{ 'digit': 5 },
6:{ 'digit': 6, '.': 3, 'e': 4 },
7:{ 'digit': 5 },
}
let state = 0;//初始状态
for (let c of s.trim()) {//循环字符串
if (c >= '0' && c <= '9') {
c = 'digit';
} else if (c === ' ') {
c = 'blank';
} else if(c === '+' || c === '-') {
c = 'sign'
}
state = graph[state][c];//返回下一个状态
if (state === undefined) {//状态转移之后不在临接表中 返回false
return false;
}
}
if (state == 3 || state == 5 || state == 6) {//状态是3、5、6中的一个说明是有效数字
return true;
}
return false;
};
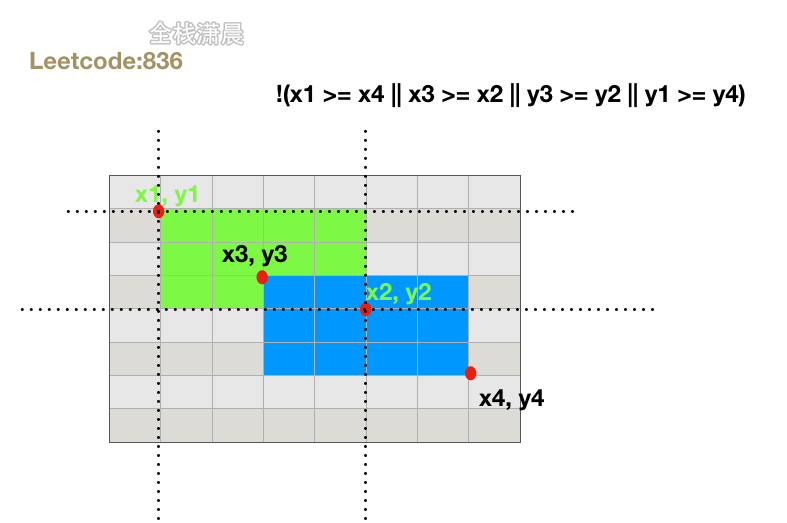
836. 矩形重叠 (easy)
- 复杂度:时间复杂度
O(1),空间复杂度O(1)
js:
var isRectangleOverlap = function(rec1, rec2) {
const [x1, y1, x2, y2] = rec1;
const [x3, y3, x4, y4] = rec2;
return !(x1 >= x4 || x3 >= x2 || y3 >= y2 || y1 >= y4);
};
java:
class Solution {
public boolean isRectangleOverlap(int[] rec1, int[] rec2) {
return !(rec1[2] <= rec2[0] || rec2[2] <= rec1[0] || rec1[3] <= rec2[1] || rec2[3] <= rec1[1]);
}
}
417. 太平洋大西洋水流问题( medium)
- 思路:准备两个表示是否能流向某个海岸线的矩阵,沿着海岸线‘’逆流而上‘’,最后统计两个大洋都能流向的坐标
- 复杂度:时间复杂度
O(m*n),m、n分别是坐标矩阵的长宽。空间复杂度O(m * n)
太平洋 ~ ~ ~ ~ ~
~ 1 2 2 3 (5) *
~ 3 2 3 (4) (4) *
~ 2 4 (5) 3 1 *
~ (6) (7) 1 4 5 *
~ (5) 1 1 2 4 *
* * * * * 大西洋
js:
var pacificAtlantic = function(matrix) {
if(!matrix || !matrix[0]) { return []; }
const m = matrix.length;
const n = matrix[0].length;
//从太平洋或大西洋逆流而上是否能到达某个坐标的数组 ture表示能流向某一个大洋
const flow1 = Array.from({ length: m }, () => new Array(n).fill(false));
const flow2 = Array.from({ length: m }, () => new Array(n).fill(false));
const dfs = (r, c, flow) => {
flow[r][c] = true;
[[r-1, c], [r+1, c], [r, c-1], [r, c+1]].forEach(([nr, nc]) => {
if(
//防止越界
nr >= 0 && nr < m &&
nc >= 0 && nc < n &&
//只有未标记的坐标才能继续递归 防止死循环
!flow[nr][nc] &&
//确保是逆流而上
matrix[nr][nc] >= matrix[r][c]
) {
dfs(nr, nc, flow)
}
})
}
//逆流而上
for(let r = 0; r<m; r+=1) {
dfs(r, 0, flow1);
dfs(r, n-1, flow2)
}
for(let c = 0; c <n; c += 1) {
dfs(0, c, flow1);
dfs(m-1, c, flow2)
}
//统计两个大洋都能流向的坐标
const res = []
for(let r = 0; r < m; r += 1) {
for(let c = 0; c < n; c += 1) {
if(flow1[r][c] && flow2[r][c]) {
res.push([r, c])
}
}
}
return res;
};
java:
public class pacificAtlantic {
private static int[][] dires = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};
private int m, n;
private int[][] matrix;
public List<List<Integer>> pacificAtlantic(int[][] matrix) {
List<List<Integer>> res = new ArrayList<>();
m = matrix.length;
if (m == 0)
return res;
n = matrix[0].length;
if (n == 0)
return res;
this.matrix = matrix;
boolean[][] canReachP = new boolean[m][n];
boolean[][] canReachA = new boolean[m][n];
for (int i = 0; i < n; i++) {
dfs(0, i, canReachP);
dfs(m - 1, i, canReachA);
}
for (int i = 0; i < m; i++) {
dfs(i, 0, canReachP);
dfs(i, n - 1, canReachA);
}
for(int i = 0; i < m; i++){
for(int j = 0; j < n; j++){
if(canReachA[i][j] && canReachP[i][j]){
List<Integer> temp = new ArrayList<>();
temp.add(i);
temp.add(j);
res.add(temp);
}
}
}
return res;
}
private void dfs(int x, int y, boolean[][] canReach) {
canReach[x][y] = true;
for (int i = 0; i < 4; i++) {
int newX = x + dires[i][0];
int newY = y + dires[i][1];
if (isIn(newX, newY) && matrix[x][y] <= matrix[newX][newY] && !canReach[newX][newY]) {
dfs(newX, newY, canReach);
}
}
}
private boolean isIn(int x, int y) {
return x >= 0 && x < m && y >= 0 && y < n;
}
}
133. 克隆图 (medium)
方法1:dfs
- 思路:深度优先遍历,递归新建每个节点和相邻节点的关系
- 复杂度:时间复杂度
O(n),n表示节点的数量。空间复杂度O(n),递归的深度
js:
var cloneGraph = function(node) {
if(!node) return;
const visited = new Map();//存放遍历过的节点
const dfs = (n) => {
const nCopy = new Node(n.val);//拷贝节点
visited.set(n, nCopy);//节点值和新建节点以键值对存入visited
(n.neighbors || []).forEach(ne => {
if(!visited.has(ne)) {
dfs(ne);//递归遍历相邻节点
}
nCopy.neighbors.push(visited.get(ne));//复制相邻节点
})
}
dfs(node);//深度优先遍历
return visited.get(node);//返回visited中的新创建的节点
};
java:
class Solution {
private HashMap <Node, Node> visited = new HashMap <> ();
public Node cloneGraph(Node node) {
if (node == null) {
return node;
}
if (visited.containsKey(node)) {
return visited.get(node);
}
Node cloneNode = new Node(node.val, new ArrayList());
visited.put(node, cloneNode);
for (Node neighbor: node.neighbors) {
cloneNode.neighbors.add(cloneGraph(neighbor));
}
return cloneNode;
}
}
方法1:bfs
- 思路:广度优先遍历每个节点,复制节点和节点间的关系
- 复杂度:时间复杂度
O(n),n表示节点的数量。空间复杂度O(n),队列的空间
js:
var cloneGraph = function(node) {
if(!node) return;
const visited = new Map();
visited.set(node, new Node(node.val));//节点值和新建节点以键值对存入visited
const q = [node];
while(q.length) {
const n = q.shift()//出队
(n.neighbors || []).forEach(ne => {//循环相邻节点
if(!visited.has(ne)) {//没有访问过就加入队列
q.push(ne);
visited.set(ne, new Node(ne.val));
}
visited.get(n).neighbors.push(visited.get(ne));//复制相邻节点
})
}
return visited.get(node);
};
java:
class Solution {
public Node cloneGraph(Node node) {
if (node == null) {
return node;
}
HashMap<Node, Node> visited = new HashMap();
LinkedList<Node> queue = new LinkedList<Node> ();
queue.add(node);
visited.put(node, new Node(node.val, new ArrayList()));
while (!queue.isEmpty()) {
Node n = queue.remove();
for (Node neighbor: n.neighbors) {
if (!visited.containsKey(neighbor)) {
visited.put(neighbor, new Node(neighbor.val, new ArrayList()));
queue.add(neighbor);
}
visited.get(n).neighbors.add(visited.get(neighbor));
}
}
return visited.get(node);
}
}
605. 种花问题 (easy)
- 思路:遍历,能种花的情况是该位置为0,前后位置不为1
- 复杂度:时间复杂度
O(n),空间复杂度O(1)
js:
var canPlaceFlowers = function (flowerbed, n) {
let count = 0
for (let i = 0, length = flowerbed.length; i < length; i++) {
//当前位置是0,并且前后都不是1,考虑在最前和最后的特殊情况
if (flowerbed[i] === 0 && flowerbed[i - 1] !== 1 && flowerbed[i + 1] !== 1) {
count++
i++
}
}
return count >= n
};
java:
class Solution {
public boolean canPlaceFlowers(int[] flowerbed, int n) {
int m = flowerbed.length;
int count = 0;
for (int i=0;i<m;i++) {
if (flowerbed[i] == 0 && (i == m - 1 || flowerbed[i + 1] == 0) && (i == 0 || flowerbed[i - 1] == 0)) {
flowerbed[i] = 1;
count++;
}
}
return count >= n;
}
}
89. 格雷编码 (medium)
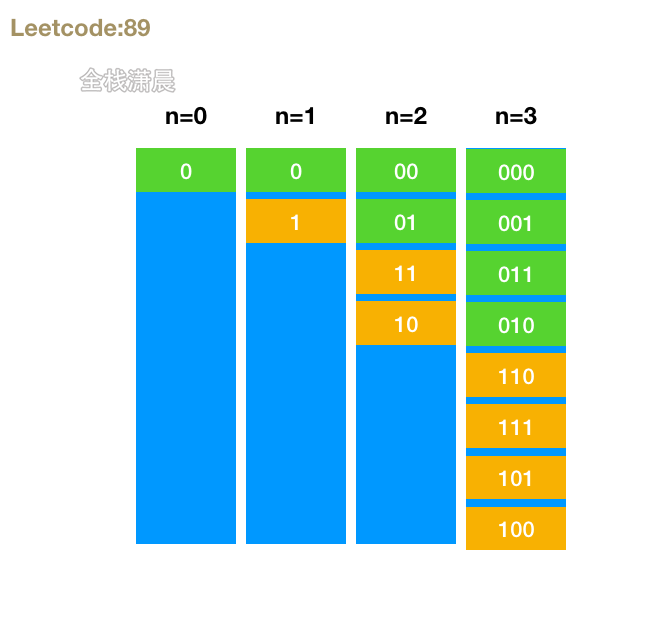
- 思路:变量pre初始为1,不断左移,ans存放结果,每次循环之前数,在前面加上pre
- 复杂度:时间复杂度
O(n^2)。空间复杂度O(1)
js:
var grayCode = function(n) {
let ans = [0];
let pre = 1;
for(let i = 0;i<n;i++){
for(let j = ans.length - 1;j>=0;j--){
ans.push(pre + ans[j]);
}
pre <<= 1;
}
return ans;
};
java:
class Solution {
public List<Integer> grayCode(int n) {
List<Integer> res = new ArrayList<Integer>() {{ add(0); }};
int head = 1;
for (int i = 0; i < n; i++) {
for (int j = res.size() - 1; j >= 0; j--)
res.add(head + res.get(j));
head <<= 1;
}
return res;
}
}
914. 卡牌分组( easy)
- 思路:统计各个数字的频次,求最大公约数是否大于1
- 复杂度:时间复杂度
O(n),空间复杂度O(n)
js:
var hasGroupsSizeX = function(deck) {
let map = new Map()
for(let n of deck){//统计频次
map.set(n,map.has(n)?map.get(n)+1:1)
}
let arr = [...map.values()]
let res = arr[0]
return arr.every(i => (res = gcd(res, i)) > 1)//求最大公约数是否大于1
};
//辗转相除法 4,2
let gcd = (a, b) => (b === 0 ? a : gcd(b, a % b))
java:
class Solution {
public boolean hasGroupsSizeX(int[] deck) {
if(deck.length == 0 || deck.length == 1) return false;
int[] count = new int[10000];
for (int num: deck) count[num]++;
return Arrays.stream(count).reduce(this::gcd).getAsInt() > 1;
}
private int gcd(int a, int b) {
return b == 0? a: gcd(b, a % b);
}
}
41. 缺失的第一个正数 (hard)
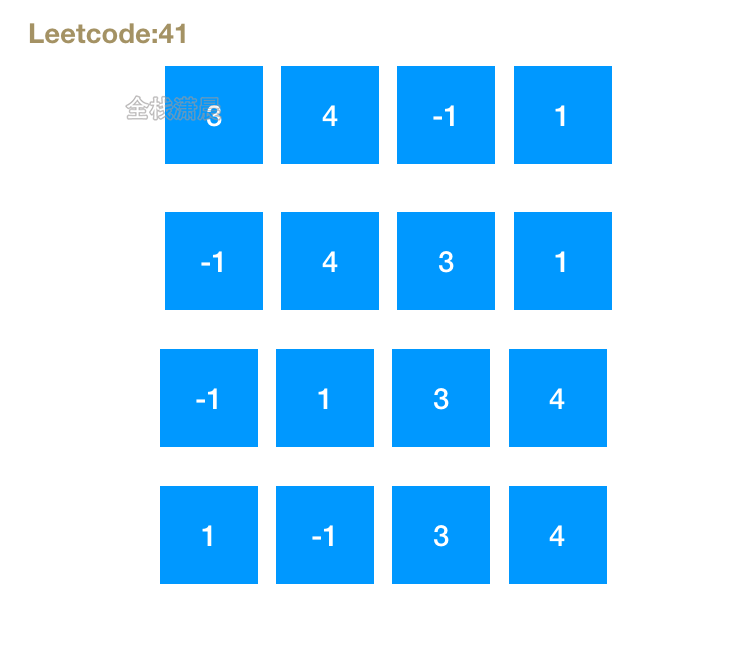
- 思路:循环nums,当前元素在
(0,nums.lenght]之间,并且nums[nums[i]-1] != nums[i],则交换位置,然后循环交换位置之后的数组,判断第一个缺失的正数 - 复杂度:时间复杂度
O(n),空间复杂度O(1)
js:
var firstMissingPositive = function(nums) {
for(let i = 0; i < nums.length; i++){
//循环nums,当前元素在(0,nums.lenght]之间,并且nums[nums[i]-1] != nums[i],则交换位置
while(nums[i] > 0 && nums[i] <= nums.length && nums[nums[i]-1] != nums[i] ){
const temp = nums[nums[i]-1];
nums[nums[i]-1] = nums[i];
nums[i] = temp;
}
}
for(let i = 0; i < nums.length; i++){//循环交换位置之后的数组,判断第一个缺失的正数
if(nums[i] != i+1){
return i+1;
}
}
// [1,2,3]
return nums.length + 1;
};
java:
class Solution {
public int firstMissingPositive(int[] nums) {
int n = nums.length;
for (int i = 0; i < n; ++i) {
while (nums[i] > 0 && nums[i] <= n && nums[nums[i] - 1] != nums[i]) {
int temp = nums[nums[i] - 1];
nums[nums[i] - 1] = nums[i];
nums[i] = temp;
}
}
for (int i = 0; i < n; ++i) {
if (nums[i] != i + 1) {
return i + 1;
}
}
return n + 1;
}
}
48. 旋转图像 (medium)

- 思路:先沿水平中轴线翻转,然后在沿主对角线翻转.
- 复杂度:时间复杂度
O(n^2),空间复杂度O(1)
js:
var rotate = function(matrix) {
const n = matrix.length;
//水平中轴线翻转
for (let i = 0; i < Math.floor(n / 2); i++) {
for (let j = 0; j < n; j++) {
[matrix[i][j], matrix[n - i - 1][j]] = [matrix[n - i - 1][j], matrix[i][j]];
}
}
//主对角线翻转
for (let i = 0; i < n; i++) {
for (let j = 0; j < i; j++) {
[matrix[i][j], matrix[j][i]] = [matrix[j][i], matrix[i][j]];
}
}
};
java:
class Solution {
public void rotate(int[][] matrix) {
int n = matrix.length;
//水平中轴线翻转
for (int i = 0; i < n / 2; ++i) {
for (int j = 0; j < n; ++j) {
int temp = matrix[i][j];
matrix[i][j] = matrix[n - i - 1][j];
matrix[n - i - 1][j] = temp;
}
}
//主对角线翻转
for (int i = 0; i < n; ++i) {
for (int j = 0; j < i; ++j) {
int temp = matrix[i][j];
matrix[i][j] = matrix[j][i];
matrix[j][i] = temp;
}
}
}
}
54. 螺旋矩阵 (medium)
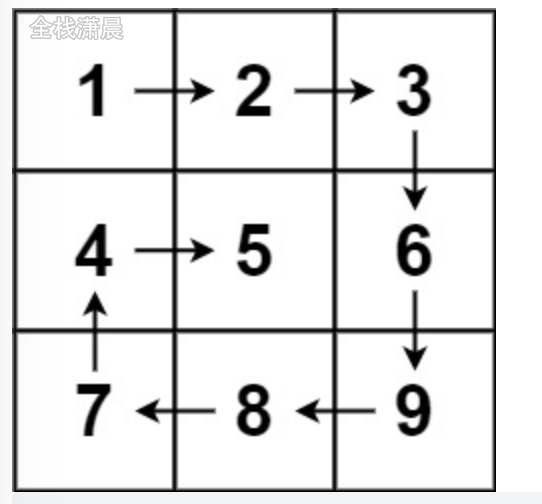
- 思路:模拟旋转的顺序
- 复杂度:时间复杂度
O(mn),空间复杂度O(1)
js:
var spiralOrder = function (matrix) {
if (matrix.length == 0) return []
const res = []
let top = 0, bottom = matrix.length - 1, left = 0, right = matrix[0].length - 1
while (top <= bottom && left <= right) {//循环条件
for (let i = left; i <= right; i++) res.push(matrix[top][i])//循环完上面一行 top++
top++
for (let i = top; i <= bottom; i++) res.push(matrix[i][right])//循环右边一行 right--
right--
if (top > bottom || left > right) break
for (let i = right; i >= left; i--) res.push(matrix[bottom][i])
bottom--
for (let i = bottom; i >= top; i--) res.push(matrix[i][left])
left++
}
return res
};
java
class Solution {
public List<Integer> spiralOrder(int[][] matrix) {
List<Integer> ans = new ArrayList<>();
int top = 0, bottom = matrix.length - 1;
int left = 0, right = matrix[0].length - 1;
while(true){
for(int i = left ; i <= right ; ++i) ans.add(matrix[top][i]);
if(++top > bottom) break;
for(int i = top ; i <= bottom ; ++i) ans.add(matrix[i][right]);
if(--right < left) break;
for(int i = right ; i >= left ; --i) ans.add(matrix[bottom][i]);
if(--bottom < top) break;
for(int i = bottom ; i >= top ; --i) ans.add(matrix[i][left]);
if(++left > right) break;
}
return ans;
}
}
56. 合并区间 (medium)
- 思路:区间按照起始位置排序,当
curr[1] >= interval[0]说明重叠,更新当前curr的右边界,如果不重,则加入result并更新区间 - 复杂度:时间复杂度
O(nlogn),排序复杂度。空间复杂度O(logn),排序额外的空间
js:
// curr: [1,3]
// interval: [2,6]
// curr: ---
// interval: -----
var merge = function (intervals) {
if (intervals.length < 2) {
return intervals;
}
intervals.sort((a, b) => a[0] - b[0]);//按照起始位置排序
let curr = intervals[0];//当前区间curr初始化为intervals[0]
let result = [];
for (let interval of intervals) {//遍历intervals
if (curr[1] >= interval[0]) {//当curr[1] >= interval[0]说明重叠
curr[1] = Math.max(curr[1], interval[1]);//更新当前curr的右边界
} else {
result.push(curr);//不重叠 加入result
curr = interval;//更新区间
}
}
result.push(curr);
return result;
};
java:
class Solution {
public int[][] merge(int[][] intervals) {
List<int[]> res = new LinkedList<>();
Arrays.sort(intervals, (o1, o2) -> Integer.compare(o1[0], o2[0]));
int start = intervals[0][0];
for (int i = 1; i < intervals.length; i++) {
if (intervals[i][0] > intervals[i - 1][1]) {
res.add(new int[]{start, intervals[i - 1][1]});
start = intervals[i][0];
} else {
intervals[i][1] = Math.max(intervals[i][1], intervals[i - 1][1]);
}
}
res.add(new int[]{start, intervals[intervals.length - 1][1]});
return res.toArray(new int[res.size()][]);
}
}
66. 加一 (easy)
- 思路:如果
digits[i] %= 10不为0,则直接返回digits,循环过程中没有reutrn掉说明一直进位到最大位置。 - 复杂度:时间复杂度
O(n),空间复杂度O(1)
js:
//例子:12,19, 99
var plusOne = function(digits) {
const len = digits.length;
for(let i = len - 1; i >= 0; i--) {
digits[i]++;
digits[i] %= 10;//求余10,覆盖当前位置
if(digits[i]!=0)//没有进位就直接返回这个数
return digits;
}
digits = [...Array(len + 1)].map(_=>0);//循环没有return掉 处理一直进位到最大位置
//[1,0,0]
digits[0] = 1;
return digits;
};
java:
class Solution {
public int[] plusOne(int[] digits) {
int len = digits.length;
for(int i = len - 1; i >= 0; i--) {
digits[i]++;
digits[i] %= 10;
if(digits[i]!=0)
return digits;
}
digits = new int[len + 1];
digits[0] = 1;
return digits;
}
}
73. 矩阵置零( medium)
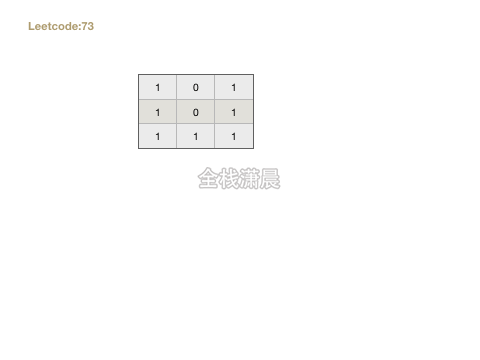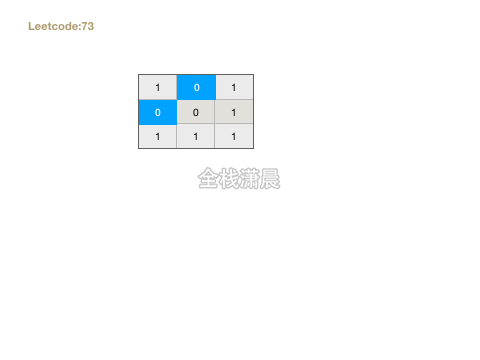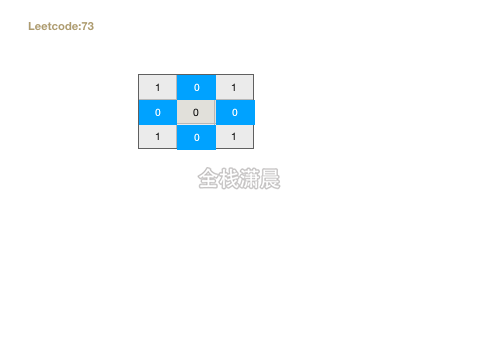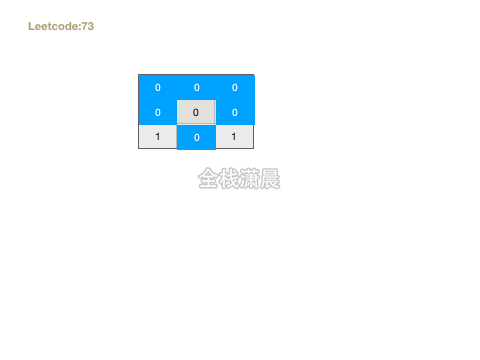
- 思路:用两个变量标记第一行和第一列是否有0,接着循环一遍矩阵,如果遇见0,将和这个网格相同的第一行和第一列的元素标记成0,在循环矩阵,如果当前网格对应的第一行和第一列是0,则将这个单元格置为0。最后如果第一列有0 ,则将这第一列全部置为0,如果第一行有0 ,则将这第一行全部置为0
- 复杂度:时间复杂度
O(mn),m、n为矩阵的行和列。空间复杂度O(1)
js:
var setZeroes = function(matrix) {
const m = matrix.length, n = matrix[0].length;
let flagCol0 = false, flagRow0 = false;//表示第一行和第一列有没有0
for (let i = 0; i < m; i++) {//寻找第一列是否存在0
if (matrix[i][0] === 0) {
flagCol0 = true;
}
}
for (let j = 0; j < n; j++) {
if (matrix[0][j] === 0) {
flagRow0 = true;
}
}
for (let i = 1; i < m; i++) {//循环矩阵,如果遇见0,将和这个网格相同的第一行和第一列的元素标记成0
for (let j = 1; j < n; j++) {
if (matrix[i][j] === 0) {
matrix[i][0] = matrix[0][j] = 0;
}
}
}
for (let i = 1; i < m; i++) {//循环矩阵,如果当前网格对应的第一行和第一列是0,则将这个单元格置为0
for (let j = 1; j < n; j++) {
if (matrix[i][0] === 0 || matrix[0][j] === 0) {
matrix[i][j] = 0;
}
}
}
if (flagCol0) {//如果第一列有0 ,则将这第一列全部置为0
for (let i = 0; i < m; i++) {
matrix[i][0] = 0;
}
}
if (flagRow0) {//如果第一行有0 ,则将这第一行全部置为0
for (let j = 0; j < n; j++) {
matrix[0][j] = 0;
}
}
};
java
class Solution {
public void setZeroes(int[][] matrix) {
int m = matrix.length, n = matrix[0].length;
boolean flagCol0 = false, flagRow0 = false;
for (int i = 0; i < m; i++) {
if (matrix[i][0] == 0) {
flagCol0 = true;
}
}
for (int j = 0; j < n; j++) {
if (matrix[0][j] == 0) {
flagRow0 = true;
}
}
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
if (matrix[i][j] == 0) {
matrix[i][0] = matrix[0][j] = 0;
}
}
}
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
if (matrix[i][0] == 0 || matrix[0][j] == 0) {
matrix[i][j] = 0;
}
}
}
if (flagCol0) {
for (int i = 0; i < m; i++) {
matrix[i][0] = 0;
}
}
if (flagRow0) {
for (int j = 0; j < n; j++) {
matrix[0][j] = 0;
}
}
}
}
419. 甲板上的战舰 (medium)
- 思路:寻找船头的个数
- 复杂度:时间复杂度
O(n^2),空间复杂度O(1)
X..X
...X
...X
js:
function countBattleships(board) {
const lenX = board.length, lenY = board[0].length
let count = 0
for (let i = 0; i < lenX; i++) {
for (let j = 0; j < lenY; j++) {
//左边和上面不是X 则是船头
if ((board[i][j] == 'X') && (i == 0 || board[i - 1][j] == '.') && (j == 0 || board[i][j - 1] == '.')) {
++count;
}
}
}
return count
};
java:
class Solution {
public int countBattleships(char[][] board) {
int count=0,i,j;
for(i=0;i<board.length;++i) {
for(j=0;j<board[0].length;++j){
if((board[i][j]=='X')&&(i==0||board[i-1][j]=='.')&&(j==0||board[i][j-1]=='.')) {
++count;
}
}
}
return count;
}
}