Python数据结构常用模块:collections、heapq、operator、itertools
heapq
堆是一种特殊的树形结构,通常我们所说的堆的数据结构指的是完全二叉树,并且根节点的值小于等于该节点所有子节点的值
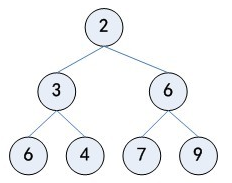
常用方法
| heappush(heap,item) | 往堆中插入一条新的值 |
| heappop(heap) | 从堆中弹出最小值 |
| heapreplace(heap,item) | 从堆中弹出最小值,并往堆中插入item |
| heappushpop(heap,item) | Python3中的heappushpop更高级 |
| heapify(x) | 以线性时间将一个列表转化为堆 |
| merge(*iterables,key=None,reverse=False) | 合并对个堆,然后输出 |
| nlargest(n,iterable,key=None) | 返回可枚举对象中的n个最大值并返回一个结果集list |
| nsmallest(n,iterable,key=None) | 返回可枚举对象中的n个最小值并返回一个结果集list |
常用方法示例
#coding=utf-8 import heapq import random def test(): li = list(random.sample(range(100),6)) print (li) n = len(li) #nlargest print ("nlargest:",heapq.nlargest(n, li)) #nsmallest print ("nsmallest:", heapq.nsmallest(n, li)) #heapify print('original list is', li) heapq.heapify(li) print('heapify list is', li) # heappush & heappop heapq.heappush(li, 105) print('pushed heap is', li) heapq.heappop(li) print('popped heap is', li) # heappushpop & heapreplace heapq.heappushpop(li, 130) # heappush -> heappop print('heappushpop', li) heapq.heapreplace(li, 2) # heappop -> heappush print('heapreplace', li)
>>> [15, 2, 50, 34, 37, 55]
>>> nlargest: [55, 50, 37, 34, 15, 2]
>>> nsmallest: [2, 15, 34, 37, 50, 55]
>>> original list is [15, 2, 50, 34, 37, 55]
>>> heapify list is [2, 15, 50, 34, 37, 55]
>>> pushed heap is [2, 15, 50, 34, 37, 55, 105]
>>> popped heap is [15, 34, 50, 105, 37, 55]
>>> heappushpop [34, 37, 50, 105, 130, 55]
>>> heapreplace [2, 37, 50, 105, 130, 55]
堆排序示例
heapq模块中有几张方法进行排序:
方法一:
#coding=utf-8 import heapq def heapsort(iterable): heap = [] for i in iterable: heapq.heappush(heap, i) return [heapq.heappop(heap) for j in range(len(heap))] if __name__ == "__main__": li = [30,40,60,10,20,50] print(heapsort(li))
>>>> [10, 20, 30, 40, 50, 60]
方法二(使用nlargest或nsmallest):
li = [30,40,60,10,20,50] #nlargest n = len(li) print ("nlargest:",heapq.nlargest(n, li)) #nsmallest print ("nsmallest:", heapq.nsmallest(n, li))
>>> nlargest: [60, 50, 40, 30, 20, 10]
>>> nsmallest: [10, 20, 30, 40, 50, 60]
方法三(使用heapify):
def heapsort(list): heapq.heapify(list) heap = [] while(list): heap.append(heapq.heappop(list)) li[:] = heap print (li) if __name__ == "__main__": li = [30,40,60,10,20,50] heapsort(li)
>>> [10, 20, 30, 40, 50, 60]
堆在优先级队列中的应用
需求:实现任务的添加,删除(相当于任务的执行),修改任务优先级
pq = [] # list of entries arranged in a heap entry_finder = {} # mapping of tasks to entries REMOVED = '<removed-task>' # placeholder for a removed task counter = itertools.count() # unique sequence count def add_task(task, priority=0): 'Add a new task or update the priority of an existing task' if task in entry_finder: remove_task(task) count = next(counter) entry = [priority, count, task] entry_finder[task] = entry heappush(pq, entry) def remove_task(task): 'Mark an existing task as REMOVED. Raise KeyError if not found.' entry = entry_finder.pop(task) entry[-1] = REMOVED def pop_task(): 'Remove and return the lowest priority task. Raise KeyError if empty.' while pq: priority, count, task = heappop(pq) if task is not REMOVED: del entry_finder[task] return task raise KeyError('pop from an empty priority queue')