机器学习之局部加权、岭回归和前向逐步回归

　　都说万事开头难，可一旦开头，就是全新的状态，就有可能收获自己未曾预料到的成果。记录是为了更好的监督、理解和推进，学习过程中用到的数据集和代码都将上传到github

　　回归是对一个或多个自变量和因变量之间的关系进行建模，求解的一种统计方法，之前的博客中总结了在线性回归中使用最小二乘法推导最优参数的过程和logistic回归，接下来将对最小二乘法、局部加权回归、岭回归和前向逐步回归算法进行依次说明和总结

1. 用线性回归找到最佳拟合曲线

（1）回归的一般方法

　　收集数据：采用任意方法收集数据

　　准备数据：回归需要数值型数据，标称型数据将被转成数值型数据

　　分析数据：绘出数据的可视化二维图将有助于对数据做出理解和分析，在采用缩减法求得新回归系数之后，可以将新拟合线绘在图上作为对比

　　训练算法：找到回归系数

　　测试算法：使用R²或者预测值和数据的拟合度，来分析模型的效果

　　使用算法：使用回归，可以在给定输入的时候预测出一个数值，这是对分类方法的提升，因为这样可以预测连续性数据而不仅仅是离散的类别标签

（2）需求

　　对dataset/ex0.txt文件中的数据集采用线性回归找到最拟合直线，数据集：https://github.com/lizoo6zhi/MachineLearn.samples/tree/master/dataset

（3）绘制数据的可视化二维图

　　

（4）通过最小二乘法得到最优参数

　　前面我们已经推导过使用最小二乘法求最优参数：

　　代码实现：

def stand_regres(dataset,label):
    """
    标准线性回归函数
    dataset:list
    label:list
    """
    X = np.mat(dataset)
    Y = np.mat(label).T

    temp = X.T * X
    if np.linalg.det(temp) == 0.0:  #计算行式的值
        print("X.T*X没有逆矩阵")
        return 
    else:
        temp = temp.I * X.T * Y
    return temp

　　注意上面代码中红色标记处，通过计算行列式的值判断X.T*X是否有逆矩阵

（5）通过计算出的最优参数对样本进行回归测试，并绘制拟合曲线

def plot_stand_regress(dataset,label,ws,ax):
    """
    绘制数据集和拟合曲线
    """
    dataset_matrix = np.mat(dataset)
    x = dataset_matrix[:,1]
    y = label
    cal_y = dataset * ws
    ax.scatter(x.T.getA(),y,s=10,c='red')
    ax.plot(x,cal_y)

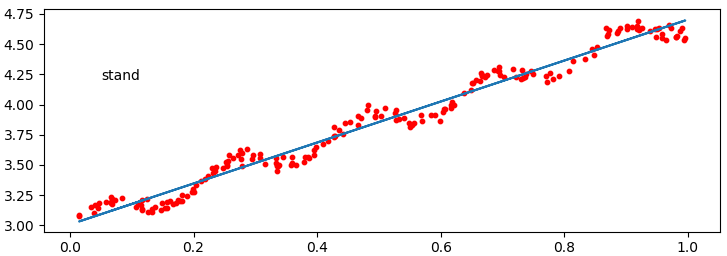
（6）在python中，NumPy库提供了相关系数的计算方法，可以通过corrcoef(yEstimate,yActual)来计算预测值与真实值的相关性

print(np.corrcoef(cal_y.T,np.mat(y)))

　　从上图可以看出，预测值与真实值之间的相关系数为0.98647356

　　最佳拟合直线方法将数据视为直线进行建模，具有十分不错的效果，但若是数据的离散程度很大呢，那该怎么办？

2. 局部加权线性回归

　　我们现实生活中的很多数据不一定都能用线性模型描述。比如房价问题，很明显直线非但不能很好的拟合所有数据点，而且误差非常大，但是一条类似二次函数的曲线却能拟合地很好。为了解决非线性模型建立线性模型的问题，我们预测一个点的值时，对这个点附近的点设置权值。基于这个思想，便产生了局部加权线性回归算法。在这个算法中，其他离一个点越近，权重越大，对回归系数的贡献就越多。损失函数如下：
　　
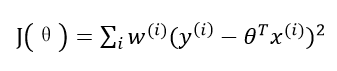
　　其中w(i)是权重，它根据要预测的点与数据集中的点的距离来为数据集中的点赋权值，当某点离要预测的点越远，其权重越小，否则越大。一个比较好的权重函数如下：

　　
 
　　该函数称为指数衰减函数，其中k为波长参数，它控制了权值随距离下降的速率，该函数形式上类似高斯分布(正态分布)，但并没有任何高斯分布的意义。该算法解出回归系数如下：

　　

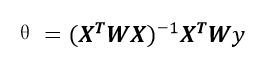
注：局部加权线性回归中的上述内容摘抄自https://blog.csdn.net/herosofearth/article/details/51969517，非常感谢作者分享！

（1）需求

　　使用局部加权线性回归对dataset/ex0.txt文件中的数据集进行曲线拟合

（2）实现

def lwrw(test_point, xarray, yarray, k = 1.0):
    """
    局部加权回归函数(locally weighted linear regression)
    dataset:list
    label:list
    """
    mat_x = np.mat(xarray)
    mat_y = np.mat(yarray).T
    row,col = np.shape(mat_x)    
    weights = np.mat(np.eye(row))
    for i in range(row):
        diffmat = test_point - mat_x[i,:]
        weights[i,i] = np.exp((diffmat*diffmat.T)/(-2.0*k*k))
    temp = mat_x.T * weights * mat_x
    if np.linalg.det(temp) == 0.0:
        print("mat_x.T * weights * X没有逆矩阵")
        return 
    else:
        temp = temp.I * mat_x.T * weights * mat_y
    return test_point*temp

（3）测试

　　分别设置k为0.01和0.003，当k=1时拟合效果和最小二乘法拟合效果一样

def plot_lwrw_regress(dataset,label,cal_y_list,ax):
    """
    绘制数据集和拟合曲线
    """
    dataset_matrix = np.mat(dataset)
    x = dataset_matrix[:,1]
    y = label
    ax.scatter(x.T.getA(),y,s=10,c='red')
    #对dataset进行排序
    sorted_index = x.argsort(0)
    sorted_x = dataset_matrix[sorted_index][:,0,:] #关键
    ax.plot(sorted_x[:,1],cal_y_list[sorted_index])

if __name__ == "__main__":
    dataset,label = load_dataset('dataset/ex0.txt')
    fig = plt.figure()
    
    #当k为0.01时
    for row in range(rows):
        cal_y = lwrw(dataset[row],dataset,label,0.01)
        x_y_map[row] = cal_y
    ax = fig.add_subplot(323)
    ax.text(0.05,4.2,'k=0.01')
    plot_lwrw_regress(dataset,label,x_y_map,ax)
    
    #当k为0.003
    for row in range(rows):
        cal_y = lwrw(dataset[row],dataset,label,0.003)
        x_y_map[row] = cal_y
    ax = fig.add_subplot(325)
    ax.text(0.05,4.2,'k=0.003')
    plot_lwrw_regress(dataset,label,x_y_map,ax)
    
    plt.show()

　　效果：

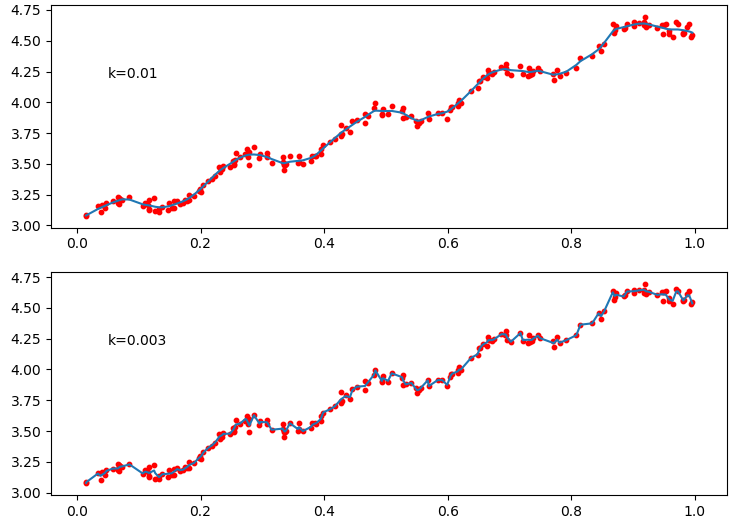
　　大家可以通过不同的k系数测试效果，局部加权线性回归存在一个问题就是增加了计算量，因为它对每个点做预测时都必须使用整个数据集

3. 岭回归

　　思考下，如果数据的特征比样本还多应该怎么办？是否还可以使用线性回归和之前的方法来做预测？

　　答案是否定的，即不能再使用前面介绍的方法，这是因为在计算（X.T*X)的逆矩阵的时候会出错

　　有逆矩阵的矩阵一定是方正，但方正不一定有逆矩阵，只有方正的行列式不为0时才有逆矩阵

　　为了解决整个问题，统计学家引入了岭回归（ridge regression）的概念，简单的说，岭回归就是在X.T * X上加一个λI使得矩阵非奇异，进而确保（X.T * X + λI）一定可逆，其中I为m*m的单位矩阵，λ是用户定义的一个数值，我们可以通过测试使用不同的λ参数来确定最优λ

　　岭回归与多项式回归唯一的不同在于代价函数上的差别。岭回归的代价函数如下：

　　

　　为了方便计算导数，通常也写成下面的形式：

　　

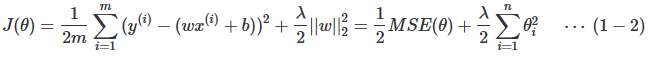
　　上式中的w是长度为n的向量，不包括截距项的系数θ0；θθ是长度为n+1的向量，包括截距项的系数θ0；m为样本数；n为特征数

　　岭回归的代价函数仍然是一个凸函数，因此可以利用梯度等于0的方式求得全局最优解（正规方程）：

　　

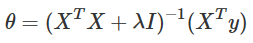
（1）需求

　　通过可视化图形描述λ与回归系数之间的关系

（2）实现

　　通过以e为底的指数函数设置λ的值，如：exp(i-10)，i为[0,30]，同公式计算不同λ下回归系数的变化

（3）代码

def ridge_regres(xarray,yarray,lam=0.2):
    """
    岭回归
    处理当特征比样本点还多，也酒水说输入数据的矩阵X不是满秩矩阵，非满秩矩阵在求逆时会出现问题
    w = (X.T*X + rI).I * X.T * Y
    """
    xmat = np.mat(xarray)
    ymat = np.mat(yarray).T
    xtx = xmat.T * xmat
    denom = xtx + np.eye(np.shape(xmat)[1])*lam
    if np.linalg.det(denom) == 0.0:
        print('denom 没有逆矩阵')
    ws = denom.I * xmat.T * ymat
    return ws
    
def ridge_test(xarray,yarray,ax):
    xmat = np.mat(xarray)
    row,col = np.shape(xmat)
    ymat = np.mat(yarray)
    xmean,xvar = data_normalize(xarray) #对数据进行标准化处理
    np.seterr(divide='ignore',invalid='ignore')
    xmat = (xmat - xmean) / xvar
    num_test_pts = 30
    wmat = np.ones((num_test_pts,col))
    
    lam_list = []
    for i in range(num_test_pts):
        lam = np.exp(i-10)
        lam_list.append(i-10)
        ws = ridge_regres(xarray,yarray,lam)
        wmat[i,:] = ws.T
    
    #绘制不同lam情况下参数变化情况
    for j in range(np.shape(wmat)[1]):
        ax.plot(lam_list,wmat[:,j])

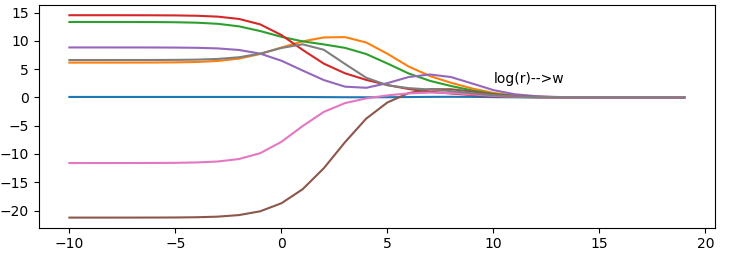
　　效果：

　　x轴为i的取值，y轴为回归系数值，从图可以看出当λ非常小时，系数和普通回归一样，当λ非常大时，所有回归系数都缩减为0，因此，我们可以在中间某处找到是的预测的结果最好的λ值

　　以下为λ=0.02的效果图

　　这样我们可以结合局部加权和岭回归计算最优回归系数，还有其他一些缩减方法，如lasso、LAR、PCA回归以及子集选择等，这些方法不仅可以提高预测精确率，而且还可以解释回归系数，将后续进行总结

　　再使用岭回归对数据集dataset/abalone.txt测试，看看回归系数变化

4. 前向逐步回归

　　前向逐步回归算法可以得到与lasso差不多的效果，但更加简单。前向回归算法属于一种贪心算法，即每一步都尽可能减少误差，一开始，所有的权重都设为1，然后每一步所作的决策是对某个权重增加或减少一个很小的值

　　伪代码如下：　

数据标准化，使其分布满足0均值和单位方差
在每轮迭代过程中：
    设置当前最小误差lowestError为正无穷
    对每个特征：
        增大或减少：
            改变一个系数得到一个新的w
            计算新w下的误差
            如果误差error小于当前最小误差：设置wbest等于当前的w
        将当前w设置为新的wbest

（1）需求

　　使用前向逐步回归算法，算出最优回归参数，并可视化显示回归参数随迭代次数的变化情况，最后标准回归算法进行比较

（2）代码实现

def stage_wise(dataset,label,step,numiter=100):
    """
    前向逐步回归
    """
    xmat = np.mat(dataset)
    xmean,xvar = data_normalize(dataset) #平均值和标准差
    ymat = np.mat(label).T
    ymat = ymat - np.mean(ymat,0)
    xmat = (xmat - xmean) / xvar
    m,n = np.shape(xmat)
    return_mat = np.zeros((numiter,n))
    ws = np.zeros((n,1))
    ws_test = ws.copy()
    ws_max = ws.copy()
    
    for iter in range(numiter):  #迭代次数
        lowest_error = np.inf
        for j in range(n):  #对每个特征进行变量
            for sign in [-1,1]:
                ws_test = ws.copy()
                ws_test[j] += step*sign
                ytest = xmat * ws_test
                rssE = ((ymat.A-ytest.A)**2).sum()
                if rssE < lowest_error:
                    lowest_error = rssE
                    ws_max = ws_test
        ws = ws_max.copy()
        return_mat[iter,:] = ws.T
    return return_mat    

def stage_wise_test(ws_mat,iternum,ax):
    """
    前向逐步回归算法中回归系数随迭代次数的变化情况
    """    
    x = range(iternum)
    for i in range(np.shape(ws_mat)[1]):
        ax.plot(x,ws_mat[:,i])

（3）测试，输出可视化效果

#前向逐步回归
ax = fig.add_subplot(326)
ws = stage_wise(dataset,label,0.01,500)
print("前向逐步回归经过迭代后的最后回归系数：",ws[-1,:])
stage_wise_test(ws,500,ax)

　　效果：

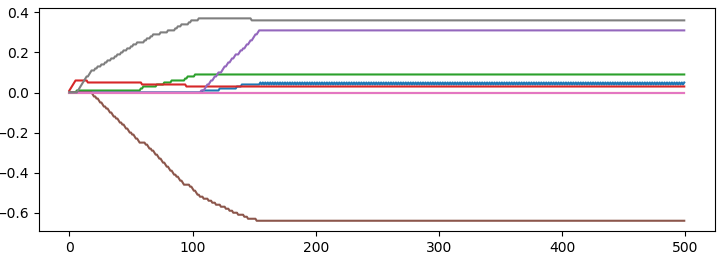
　　上图表示了回归系数随迭代次数的变化情况，当迭代150次时，回归系数稳定分别为：

（4）接下来使用标准回归算法，也就是最小二乘法对dataset/abalone.txt数据集进行测试，计算回归系数

    #使用标准回归对"dataset/abalone.txt"数据集进行测试
    #对数据进行标准化处理
    xman,xvar = data_normalize(dataset)
    xmat = np.mat(dataset)
    xmat = (xmat - xman) / xvar
    ymat = np.mat(label)
    ax = stand_regres(xmat,ymat)
    print("标准回归后得到的回归系数：",ws[-1,:])

　　最终输出结果和前向逐步回归算出系数一样：

5. 总结

　　与分类一样，回归也是预测目标值的过程，回归与分类的不同点在于，前者预测连续性变量，而后者预测离散型变量，回归是统计学中最有力的工具之一，在回归方程里，求得特征对应的最佳回归系数的方法是最小 化误差的平方和，给定输入的矩阵X，如果X.T * X的逆存在并可以求得的化，回归法可以直接使用，数据集上计算出的回归方程并不一定意味着它是最佳的，可以使用预测值yHat和原始值y的相关性来度量回归方程的好坏。　

　　当数据的样本数比特征数还少的时候，矩阵X.T * X的逆不能直接计算，即便当样本数比特征数多时，X.T * X的逆仍可能无法直接计算，这是因为特征有可能高度相关，这时可以考虑使用岭回归，因为当X.T * X的逆不能计算时，它仍保证能求得回归系数

　　岭回归是缩减法的一种，相当于对回归系数的大小施加了限制，另一种很好的缩减法是lasso,lasso难以求解，但可以 使用计算简便的逐步线性回归方法来求得近似解

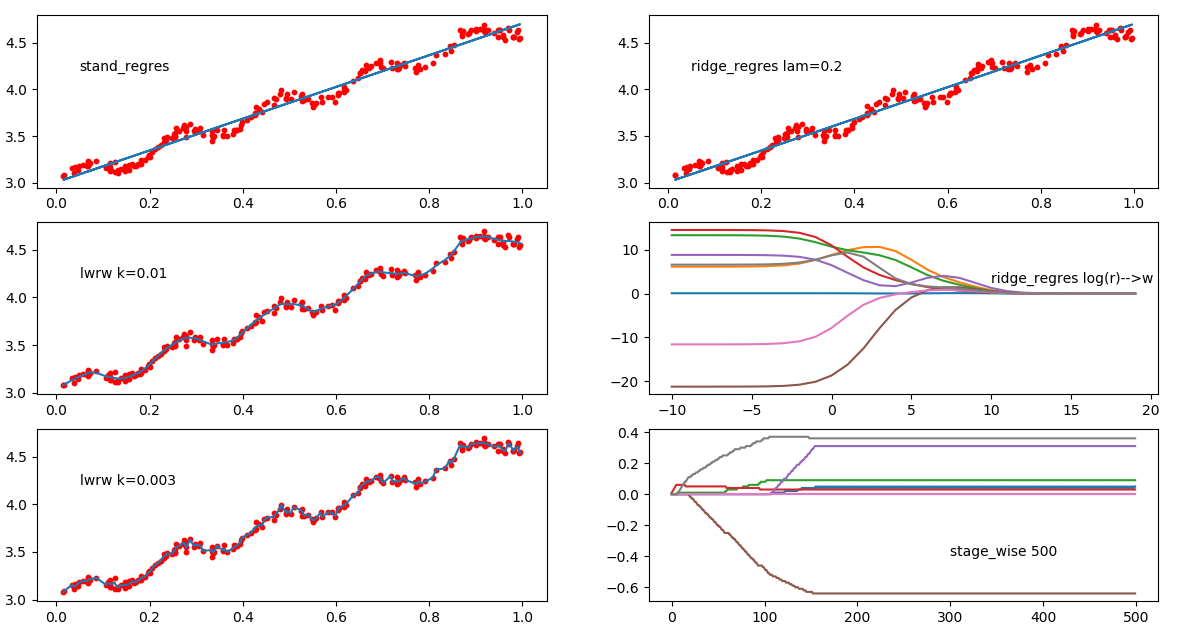
　　最后来张综合图：