K-近邻算法（python）

K-近邻算法

优点：精度高、对异常值不敏感、无数据输入假定。

缺点：计算复杂度高、空间复杂度高。

适用范围：数值型和离散型（标称型）。

工作原理：

       存在一个样本数据集合，也称训练样本集，并且样本集中每个数据都存在标签，即我们知道样本集中每一数据与所属分类的对应关系。输入没有标签的新数据后，将新数据的每个特征与样本集中数据对应的特征进行比较，然后算法提取样本集中特征最相似数据（最邻近）的分类标签。一般来说，我们只选择样本集中前K个最相似的数据，这就是K-近邻算法中K的出处，通常K是不大于20的整数。最后，选择K个最相似数据中出现次数最多的分类，最为新数据的分类。

对预测的每条数据依次执行以下操作：

（1）计算已知类别数据集中的点与当前点之间的距离

（2）按照距离递增依次排序

（3）选取与当前点距离最小的K个点

（4）确定前K个点所在的类别出现的频率

（5）返回前K个点出现频率最高的类别作为当前点的预测分类。

sklearn中KNeighborsClassifier的介绍

class sklearn.neighbors.KNeighborsClassifier(n_neighbors=5, weights=‘uniform’, algorithm=‘auto’, leaf_size=30, p=2, metric=‘minkowski’, metric_params=None, n_jobs=None, **kwargs)

n_neighbors: int, 可选参数(默认为 5)
  用于kneighbors查询的默认邻居的数量
weights（权重）: str or callable(自定义类型), 可选参数(默认为 ‘uniform’)
  用于预测的权重函数。可选参数如下:

       ‘uniform’ : 统一的权重. 在每一个邻居区域里的点的权重都是一样的。
       ‘distance’ : 权重点等于他们距离的倒数。使用此函数，更近的邻居对于所预测的点的影响更大。
　　[callable] : 一个用户自定义的方法，此方法接收一个距离的数组，然后返回一个相同形状并且包含权重的数组。

algorithm（算法）: {‘auto’, ‘ball_tree’, ‘kd_tree’, ‘brute’}, 可选参数（默认为 ‘auto’）
  计算最近邻居用的算法：

　　‘ball_tree’ 使用算法BallTree
　　‘kd_tree’ 使用算法KDTree
　　‘brute’ 使用暴力搜索.
　　‘auto’ 会基于传入fit方法的内容，选择最合适的算法。

  注意 : 如果传入fit方法的输入是稀疏的，将会重载参数设置，直接使用暴力搜索。
leaf_size（叶子数量）: int, 可选参数(默认为 30)
  传入BallTree或者KDTree算法的叶子数量。此参数会影响构建、查询BallTree或者KDTree的速度，以及存储BallTree或者KDTree所需要的内存大小。 此可选参数根据是否是问题所需选择性使用。
p: integer, 可选参数(默认为 2)
  用于Minkowski metric（闵可夫斯基空间）的超参数。p = 1, 相当于使用曼哈顿距离 (l1)，p = 2, 相当于使用欧几里得距离(l2)  对于任何 p ，使用的是闵可夫斯基空间(l_p)
metric（矩阵）: string or callable, 默认为 ‘minkowski’
  用于树的距离矩阵。默认为闵可夫斯基空间，如果和p=2一块使用相当于使用标准欧几里得矩阵. 所有可用的矩阵列表请查询 DistanceMetric 的文档。
metric_params（矩阵参数）: dict, 可选参数(默认为 None)
  给矩阵方法使用的其他的关键词参数。
n_jobs: int, 可选参数(默认为 1)
  用于搜索邻居的，可并行运行的任务数量。如果为-1, 任务数量设置为CPU核的数量。不会影响fit方法。
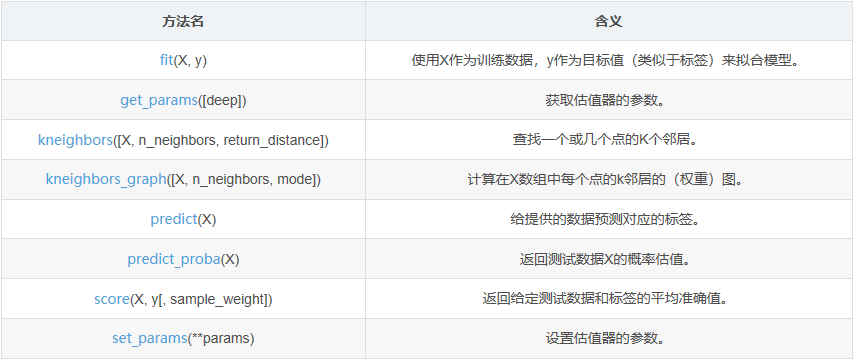
KNeighborsClassifier的方法（官方文译）

 

K值选择

• 如果选择较小的K值，就相当于用较小的领域中的训练实例进行预测，“学习”近似误差会减小，只有与输入实例较近或相似的训练实例才会对预测结果起作用，与此同时带来的问题是“学习”的估计误差会增大，换句话说，K值的减小就意味着整体模型变得复杂，容易发生过拟合；
• 如果选择较大的K值，就相当于用较大领域中的训练实例进行预测，其优点是可以减少学习的估计误差，但缺点是学习的近似误差会增大。这时候，与输入实例较远（不相似的）训练实例也会对预测启作用，使预测发生错误，且K值的增大就意味着整体的模型变得简单。
• K=N，则完全不足取，因为此时无论输入实例是什么，都只是简单的预测它属于在训练实例中最多的类，模型过于简单，忽略了训练实例中大量有用信息。

在实际应用中，K值一般取一个比较小的数值，例如采用交叉验证法（简单来说，就是一部分样本做训练集，一部分做测试集）来选择最优的K值。

1、使用sklearn的K-近邻算法的鸢尾花数据应用，数据来源：程序内置。

import numpy as np
from sklearn.neighbors import KNeighborsClassifier #k邻近算法模型
#使用datasets创建数据
import sklearn.datasets as datasets
iris = datasets.load_iris()
#将Sepal.Length,Sepal.Width,Petal.Length    ,Petal.Width的值取出
feature = iris['data']
#将Species的值取出
target = iris['target']
#利用random进行随机打乱且固定随机因子,使数据保持对应关系
#使用相同的seed()值，则每次生成的随即数都相同,且只一次有效
np.random.seed(1)
#参数可以是数组或列表，打乱他们的顺序
np.random.shuffle(feature)
np.random.seed(1)
np.random.shuffle(target)
#训练数据,取打乱后的前140行
#从第0行到第140行
x_train = feature[:140]
y_train = target[:140]
#测试数据，取打乱后的后十行
x_test = feature[-10:]
y_test =target[-10:]
#实例化模型对象&训练模型，n_neighbors邻居的数量（默认为5）
knn = KNeighborsClassifier(n_neighbors=10)
knn.fit(x_train,y_train)
k=knn.score(x_train,y_train)
print('训练数据的平均准确值：',k)
print('预测分类：',knn.predict(x_test))
print('真实分类：',y_test)

结果：

训练数据的平均准确值： 0.9785714285714285
预测分类： [0 2 1 2 1 2 2 1 2 0]
真实分类： [0 2 1 2 1 2 2 1 2 0]

2、使用sklearn的K-近邻算法的二维坐标轴数据分类，数据来源：《机器学习实战》

import numpy as np
from sklearn.neighbors import KNeighborsClassifier 
#手动创建训练数据集,在坐标轴上的四个点，分别是A,A,B,B
feature = np.array([[1.0,1.1],[1.0,1.0],[0.0,0.0],[0.0,0.1]])
target = np.array(['A','A','B','B'])
#实例k邻近模型，指定k值=3
knn = KNeighborsClassifier(n_neighbors=3)
#训练数据
knn.fit(feature,target)
#模型评分
s=knn.score(feature,target)
print(s)
#预测
p=knn.predict(np.array([[0.2,0.3]]))
print(p)

结果：

1.0
['B']

3、使用sklearn的K-近邻算法对图片格式bmp数据处理和分类，数据下载地址：https://github.com/angleboygo/data_ansys

import numpy as np 
import matplotlib.pyplot as plt
from sklearn.neighbors import KNeighborsClassifier
img=plt.imread('F://python入门//文件//knn//0//0_2.bmp')
plt.imshow(img)
print('图片的形状：',img.shape)
feature=[]
target=[]
for i in range(10):
    for j in range(500):
        img_arr=plt.imread(f'F://python入门//文件//knn/{i}//{i}_{j+1}.bmp')
        feature.append(img_arr)
        target.append(i)
#构建特征数据格式
feature=np.array(feature)
target=np.array(target)
#(5000, 28, 28)
print('feature的形状：',feature.shape) 
#输入数据必须是二维数组,必须对feature降维
#(1)降维方式一:mean() (2)降维方式二:reshape()
feature=feature.reshape(5000,28*28)
#将样本打乱,固定随机因子,使数据保持对应关系
np.random.seed(5)
np.random.shuffle(feature)
np.random.seed(5)
np.random.shuffle(target)
#数据分割为训练数据和测试数据
x_train=feature[:4950]
y_train=target[:4950]
x_test=feature[-50:]
y_test=target[-50:]
#训练模型
knn = KNeighborsClassifier(n_neighbors=8)
knn.fit(x_train,y_train)
#评分
s = knn.score(x_train,y_train)
print('模型评分：',s)
#预测
p = knn.predict(x_test)
print('y的预测值（分类）：',p)
print('y的真实值（分类）：',y_test)

结果：

图片的形状： (28, 28)
feature的形状： (5000, 28, 28)
模型评分： 0.9482828282828283
y的预测值（分类）： [0 1 0 7 8 2 8 0 0 0 8 9 5 5 3 6 4 7 4 1 6 8 3 0 0 2 1 7 1 7 6 0 2 6 2 6 8
 7 5 5 4 3 1 2 4 6 1 8 4 5]
y的真实值（分类）： [0 1 0 7 8 2 8 0 0 0 8 9 5 5 3 6 4 7 4 1 6 8 3 0 0 2 4 7 4 7 6 0 2 6 8 6 8
 7 5 5 4 3 1 2 4 6 3 8 4 5]