简单实系数一元多项式问题

数据结构与算法实验题 2.2 简单实系数一元多项式问题

★问题描述：

★数据输入：

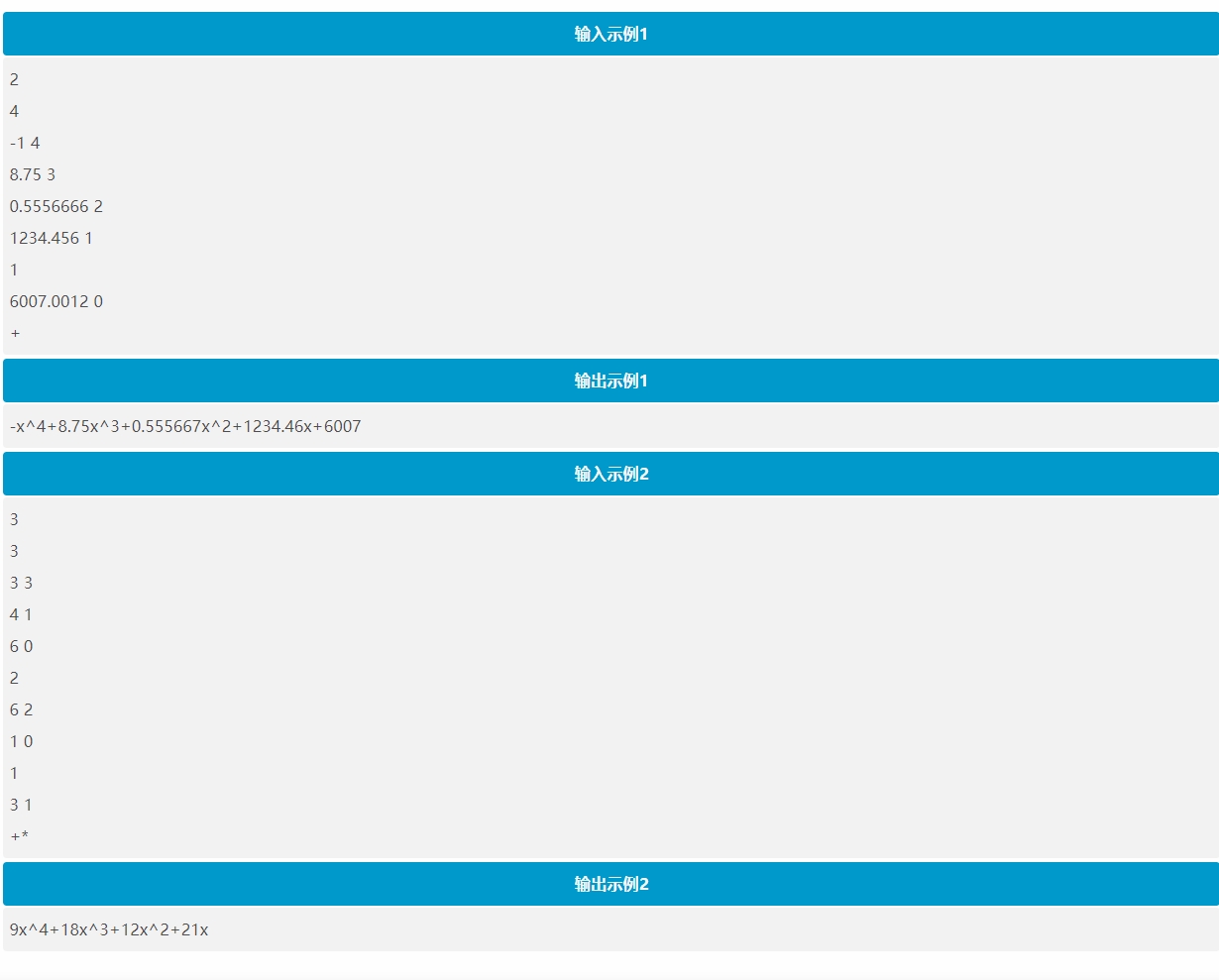
第一行有一个正整数 k，表示有 k 个一元实系数多项式。接下来有 k(k<=20)个数据块，每个数据块的第 1行是 1 个正整数 s，表示该数据块共有 s行。接下来的 s 行中，每行由实数 a和整数 b组成，表示多项式中的项 axbaxb 。紧接着 k 个数据块的是长度为 k-1 的字符串，每个字符是“+”，“-”，“*”这 3 个字符之一。

★数据输出:

文件的第一行是计算得到的多项式 g(x)，输出多项式时，xkxk 用 x^k 表示。例如，5xk5xk 应表示为 5x^5。注意输出的结果应该符合数学中手写习惯。例如，x不应输出为 1x^1,实系数 保留 6位有效数字。(数据保证多项式项数不大于 500)

★补充说明

整数 b 满足 b 为非负整数

输出的多项式结果，按项的幂次从高到低排序，参见样例

★Hint

c++中可以使用 setprecision 操作符来控制显示浮点数值的有效数的数量

该题主要使用数组模拟运算，详细注释如下

#include<iostream>
#include<cstring>
#include<cmath>
using namespace std;
double a[22][51000];
//构建二维数组，如a[m][n]=j代表第m个多项式的第n次方项（幂次(指数)为n的项）的系数为j;(即次幂为n的项为 j*x^n)
//比如第2个多项式的5*x^6就应该表示为a[2][6]=5;
double b[51000];//数组b用来存乘法运算的结果
//数组下标代表指数（次幂），b[m]=n 代表指数为m的项的系数为n;

int main() {
	int k, t, y, ymax = 0;
	double x;

	//数据输入
	scanf("%d", &k);//代表具有k个多项式，k个数据块
	for (int i = 1; i <= k; i++) {
		cin >> t;//表明该数据块共有t行
		while (t--) {//输入t次
			cin >> x >> y;
			a[i][y] = x;//代表第i个多项式的y次方项的系数为x;
			if (y > ymax) ymax = y;//ymax用来记录最高的指数，即最高次幂
		}
	}
	char temp[510];
	for (int i = 1; i <= k - 1; i++) {
		cin >> temp[i];//输入运算符
	}

	//多项式运算
	for (int i = 1; i <= k - 1; i++) {
		if (temp[i] == '+') {
			for (int j = 0; j <= ymax; j++) {
				a[i + 1][j] += a[i][j];//指数从零到ymax，将两个多项式指数相同的项相加，并将结果存在后一个多项式中
				//将结果存在后一个多项式，是因为运算后的结果可能还要与下一个多项式进行下一次运算
			}
		}
		if (temp[i] == '-') {
			for (int j = 0; j <= ymax; j++) {
				a[i + 1][j] = a[i][j] - a[i + 1][j];
				//和运算‘+’相似，只不过把“相加” 变为 “相减”
			}
		}
		if (temp[i] == '*') {
			int t = ymax;
			memset(b, 0, sizeof(b));//将数组b清零，因为乘法运算可能不止一次，所以每一次都要将数组b清零
			for (int j = 0; j <= t; j++) {
				for (int m = 0; m <= t; m++) {
					b[j + m] += a[i][j] * a[i + 1][m];//由于  x^j * x^m=x^(j+m),所以将系数的运算结果存到b[j+m]
					if (j + m > ymax && b[j + m]) ymax = j + m;//如果运算结果产生的新项的指数大于ymax，就更新ymax
				}
			}
			for (int j = 0; j <= ymax; j++) {
				a[i + 1][j] = b[j];//将运算结果放回参与运算的两个多项式中的第二个多项式
				//cout << b[j] << " ";
			}
		}
	}


	//数据输出
	//数据输出需要考虑最高项的输出（即首先输出的项）和其他项的输出
	//还需要考虑系数和指数为“+1、-1”时输出的情况，还有系数为大于0时要输出“+”


	//最高项输出的分类讨论
	while (a[k][ymax] == 0 && ymax) {//如果最高项为0的话就跳过
		ymax--;
	}
	if (ymax != 1 && ymax != 0) {//但次幂为1和0的时候需要特判
		if (a[k][ymax] == 1) {//如果系数为1不输出系数
			cout << "x^" << ymax;
		}
		else if (a[k][ymax] == -1) {//系数为-1只输出负号
			cout << "-x^" << ymax;
		}
		else {
			cout << a[k][ymax] << "x^" << ymax;//其他情况正常输出
		}
	}
	else if (ymax == 1) {//只输出x，不输出指数
		if (a[k][ymax] == 1) {//当系数为1时不输出系数
			cout << "x";
		}
		else if (a[k][ymax] == -1) {//系数为-1时只输出负号
			cout << "-x";
		}
		else {
			cout << a[k][ymax] << "x";//其他情况正常输出
		}
	}
	else {
		cout << a[k][ymax];//当最高次幂为0时直接输出系数
	}

	//除最高项的输出
	for (int i = ymax - 1; i >= 0; i--) {
		if (a[k][i] > 0) cout << '+';//如果系数为正，需要输出‘+’
		if (fabs(a[k][i] - 0) > 0.000001) {//即当a[k][i]!=0时
			if (a[k][i] != 1 && a[k][i] != -1) {
				cout << a[k][i];//系数不为正负一时直接输出
			}
			else {
				if (i == 0) {
					cout << a[k][i];//指数为0时只输出系数
				}
			}
			if (a[k][i] == -1) cout << '-';//系数为-1的特判
			if (i > 1) {
				cout << "x^" << i;
			}
			if (i == 1) {
				cout << 'x';//指数为1的特判
			}
		}
	}
	return 0;
}