[BZOJ2154]Crash的数字表格

[BZOJ2154]Crash的数字表格

试题描述

今天的数学课上，Crash小朋友学习了最小公倍数(Least Common Multiple)。对于两个正整数a和b，LCM(a, b)表示能同时被a和b整除的最小正整数。例如，LCM(6, 8) = 24。回到家后，Crash还在想着课上学的东西，为了研究最小公倍数，他画了一张N*M的表格。每个格子里写了一个数字，其中第i行第j列的那个格子里写着数为LCM(i, j)。一个4*5的表格如下： 1 2 3 4 5 2 2 6 4 10 3 6 3 12 15 4 4 12 4 20 看着这个表格，Crash想到了很多可以思考的问题。不过他最想解决的问题却是一个十分简单的问题：这个表格中所有数的和是多少。当N和M很大时，Crash就束手无策了，因此他找到了聪明的你用程序帮他解决这个问题。由于最终结果可能会很大，Crash只想知道表格里所有数的和mod 20101009的值。

输入

输入的第一行包含两个正整数，分别表示N和M。

输出

输出一个正整数，表示表格中所有数的和mod 20101009的值。

输入示例

4 5

输出示例

122

数据规模及约定

100%的数据满足N, M ≤ 10^7。

题解

把最小公倍数转化成最大公约数，因为我们比较熟悉最大公约数。

然后考虑枚举 gcd(x, y)

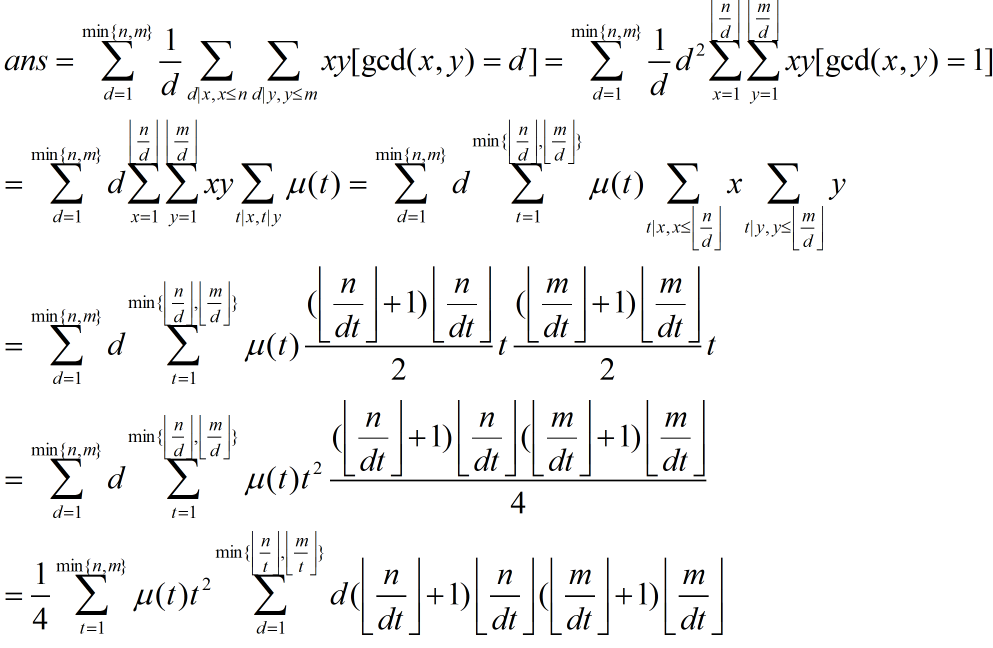
于是

于是分两个 sqrt(n) 分别计算 f(n, m) 和 ans 就好了。

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cctype>
#include <algorithm>
using namespace std;

const int BufferSize = 1 << 16;
char buffer[BufferSize], *Head, *Tail;
inline char Getchar() {
	if(Head == Tail) {
		int l = fread(buffer, 1, BufferSize, stdin);
		Tail = (Head = buffer) + l;
	}
	return *Head++;
}
int read() {
	int x = 0, f = 1; char c = Getchar();
	while(!isdigit(c)){ if(c == '-') f = -1; c = Getchar(); }
	while(isdigit(c)){ x = x * 10 + c - '0'; c = Getchar(); }
	return x * f;
}

#define maxn 10000001
#define MOD 20101009
#define div4 15075757
#define LL long long

int n, m, prime[maxn], cp, mu[maxn], sum[maxn], tot[maxn];
bool vis[maxn];
void init() {
	mu[1] = 1; sum[1] = 1;
	for(int i = 2; i <= n; i++) {
		if(!vis[i]) prime[++cp] = i, mu[i] = MOD - 1;
		for(int j = 1; i * prime[j] <= n && j <= cp; j++) {
			vis[i*prime[j]] = 1;
			if(i % prime[j] == 0){ mu[i*prime[j]] = 0; break; }
			mu[i*prime[j]] = -mu[i];
			if(mu[i*prime[j]] < 0) mu[i*prime[j]] += MOD;
		}
		sum[i] = sum[i-1] + (LL)mu[i] * i % MOD * i % MOD;
		if(sum[i] >= MOD) sum[i] -= MOD;
	}
	for(int i = 1; i <= n; i++) {
		tot[i] = tot[i-1] + i;
		if(tot[i] >= MOD) tot[i] -= MOD;
	}
	return ;
}

int f(int n, int m) {
	int ans = 0;
	for(int i = 1, lst; i <= n; i = lst + 1) {
		lst = min(n / (n / i), m / (m / i));
		ans += (LL)(n / i + 1) * (n / i) % MOD * (m / i + 1) % MOD * (m / i) % MOD * (tot[lst] - tot[i-1] + MOD) % MOD;
		if(ans >= MOD) ans -= MOD;
	}
	return ans;
}

int main() {
	n = read(); m = read(); int ans = 0;
	if(n > m) swap(n, m);
	init();
	for(int i = 1, lst; i <= n; i = lst + 1) {
		lst = min(n / (n / i), m / (m / i));
		ans += (LL)f(n / i, m / i) * (sum[lst] - sum[i-1] + MOD) % MOD;
		if(ans >= MOD) ans -= MOD;
	}
	printf("%lld
", (LL)ans * div4 % MOD);
	
	return 0;
}

UPD：

其实 μ(t)·t² 的前缀和可以杜教筛的。把 μ(t)·t² 和 t² 狄利克雷卷积一下，得到

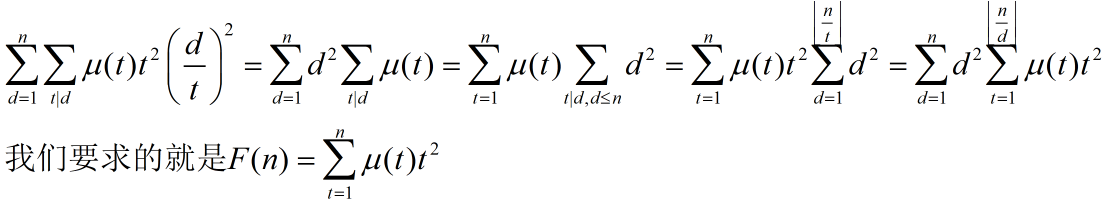
于是就可以扩大数据范围了。。。

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cctype>
#include <algorithm>
using namespace std;

int read() {
	int x = 0, f = 1; char c = getchar();
	while(!isdigit(c)){ if(c == '-') f = -1; c = getchar(); }
	while(isdigit(c)){ x = x * 10 + c - '0'; c = getchar(); }
	return x * f;
}

#define maxn 1000000
#define MOD 998244353
#define div6 166374059
#define LL long long

int prime[maxn], cp, mu[maxn], smu[maxn];
bool vis[maxn];
void init() {
	mu[1] = 1;
	for(int i = 2; i < maxn; i++) {
		if(!vis[i]) prime[++cp] = i, mu[i] = -1;
		for(int j = 1; i * prime[j] < maxn && j <= cp; j++) {
			vis[i*prime[j]] = 1;
			if(i % prime[j] == 0){ mu[i*prime[j]] = 0; break; }
			mu[i*prime[j]] = -mu[i];
		}
	}
	for(int i = 1; i < maxn; i++) {
		mu[i] *= (LL)i * i % MOD;
		if(mu[i] < 0) mu[i] += MOD;
		smu[i] = smu[i-1] + mu[i];
		if(smu[i] >= MOD) smu[i] -= MOD;
	}
	return ;
}

#define MODs 1000007

struct Hash {
	int ToT, head[MODs], nxt[maxn], val[maxn], sum[maxn];
	
	Hash() { ToT = 0; memset(head, 0, sizeof(head)); }
	
	int Find(int x) {
		int u = x % MODs;
		for(int e = head[u]; e; e = nxt[e]) if(val[e] == x) return sum[e];
		return -1;
	}
	void Insert(int x, int v) {
		int u = x % MODs;
		nxt[++ToT] = head[u]; val[ToT] = x; sum[ToT] = v; head[u] = ToT;
		return ;
	}
} hh;

int sum_sqr(int n) { return (LL)n * (n + 1) % MOD * (n << 1 | 1) % MOD * div6 % MOD; }
int Sum(int n) {
	if(n < maxn) return smu[n];
	if(hh.Find(n) >= 0) return hh.Find(n);
	int sum = 1;
	for(int i = 2, lst; i <= n; i = lst + 1) {
		lst = n / (n / i);
		sum -= (LL)(sum_sqr(lst) - sum_sqr(i - 1) + MOD) * Sum(n / i) % MOD;
		if(sum < 0) sum += MOD;
	}
	hh.Insert(n, sum);
	return sum;
}

int sum_num(int n) { return ((LL)n * (n + 1) >> 1) % MOD; }
int calc(int n, int m) { return ((LL)(n + 1) * n >> 1) % MOD * (((LL)(m + 1) * m >> 1) % MOD) % MOD; }
int f(int n, int m) {
	int ans = 0;
	for(int i = 1, lst; i <= n; i = lst + 1) {
		lst = min(n / (n / i), m / (m / i));
		ans += (LL)(sum_num(lst) - sum_num(i - 1) + MOD) * calc(n / i, m / i) % MOD;
		if(ans >= MOD) ans -= MOD;
	}
	return ans;
}

int main() {
	init();
	
	int n = read(), m = read();
	if(n > m) swap(n, m);
	
	int ans = 0;
	for(int i = 1, lst; i <= n; i = lst + 1) {
		lst = min(n / (n / i), m / (m / i));
		ans += (LL)(Sum(lst) - Sum(i - 1) + MOD) * f(n / i, m / i) % MOD;
		if(ans >= MOD) ans -= MOD;
	}
	
	printf("%d
", ans);
	
	return 0;
}