[BZOJ2820]YY的GCD

[BZOJ2820]YY的GCD

试题描述

神犇YY虐完数论后给傻×kAc出了一题给定N, M,求1<=x<=N, 1<=y<=M且gcd(x, y)为质数的(x, y)有多少对kAc这种

傻×必然不会了，于是向你来请教……多组输入

输入

第一行一个整数T 表述数据组数接下来T行，每行两个正整数，表示N, M

输出

T行，每行一个整数表示第i组数据的结果

输入示例

2
10 10
100 100

输出示例

30
2791

数据规模及约定

T = 10000
N, M <= 10000000

题解

设

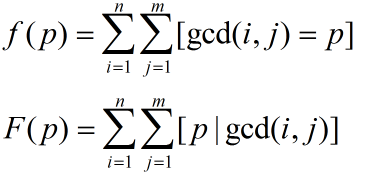
易知

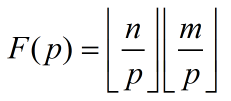……式1

根据莫比乌斯反演有

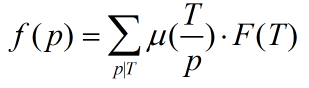……式2

根据 式1 和 式2 可得

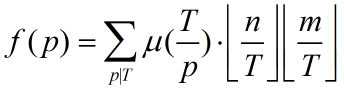
我们要求这个

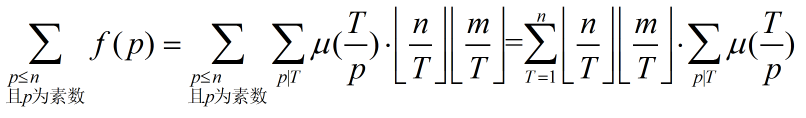
不妨令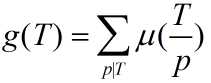，那么我们可以用线性筛求出每一个 g(T)，递推式如下：（对于一个质数 k）

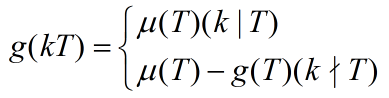
然后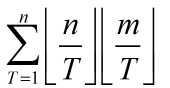这部分我们可以分块计算，即将所有相同的 [n/T][m/T] 利用乘法分配律只计算一次，这样就不会被卡成暴力了。

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>
using namespace std;

const int BufferSize = 1 << 16;
char buffer[BufferSize], *Head, *Tail;
inline char Getchar() {
    if(Head == Tail) {
        int l = fread(buffer, 1, BufferSize, stdin);
        Tail = (Head = buffer) + l;
    }
    return *Head++;
}
int read() {
    int x = 0, f = 1; char c = Getchar();
    while(!isdigit(c)){ if(c == '-') f = -1; c = Getchar(); }
    while(isdigit(c)){ x = x * 10 + c - '0'; c = Getchar(); }
    return x * f;
}

#define maxn 10000010
#define LL long long
int T, n, m;

int prime[maxn], cnt, u[maxn], g[maxn];
LL sum[maxn];
bool vis[maxn];
void u_table() {
	int N = maxn - 10;
	u[1] = 1; g[1] = 0;
	for(int i = 2; i <= N; i++) {
		if(!vis[i]) prime[++cnt] = i, u[i] = -1, g[i] = 1;
		for(int j = 1; j <= cnt && (LL)prime[j] * (LL)i <= (LL)N; j++)
			if(i % prime[j]) vis[i*prime[j]] = 1, u[i*prime[j]] = -u[i], g[i*prime[j]] = u[i] - g[i];
			else{ vis[i*prime[j]] = 1, u[i*prime[j]] = 0, g[i*prime[j]] = u[i]; break; }
	}
	for(int i = 1; i <= N; i++) sum[i] = sum[i-1] + (LL)g[i];
	return ;
}

int main() {
	u_table();
	T = read();
	
	while(T--) {
		n = read(); m = read();
		if(n > m) swap(n, m);
		int p = 1;
		LL ans = 0;
		for(; p <= n;) {
			int np = p;
			p = min(n / (n / np), m / (m / np));
			ans += (sum[p] - sum[np-1]) * (LL)(n / np) * (LL)(m / np);
			p++;
		}
		printf("%lld
", ans);
	}
	
	return 0;
}