前两篇博客整理了双 FIFO 生成 3x3 矩阵的方法,本篇博客整理一下 Quartus II 软件下的 shift ip 核及如何生成 3x3 矩阵。
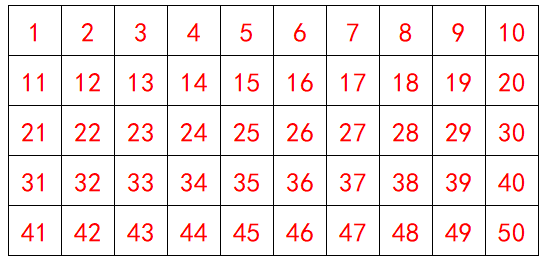
要求:模拟一张分辨率为 10x5 的图片,图片的数据为 1~50,用 Verilog 对其生成 3x3 矩阵,以便后面的图像处理。
testbench:数据的使能和数据对齐,每隔 10 个数据就空闲小段时间,每隔 50 个数据又空闲一段时间,模仿图像帧的样子,如下所示:

一、Shift IP 核原理解析
还是直接拿官方例程来说明吧。在官方手册上,展示了一个案例,首先是配置说明:

这段配置在 Shift ip 核中的具体设置如下图所示:
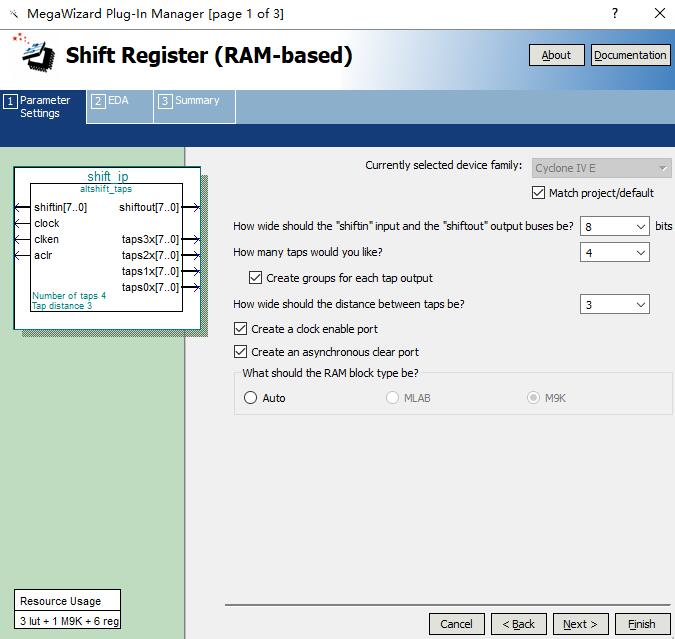
由此进行仿真可得到如下波形:
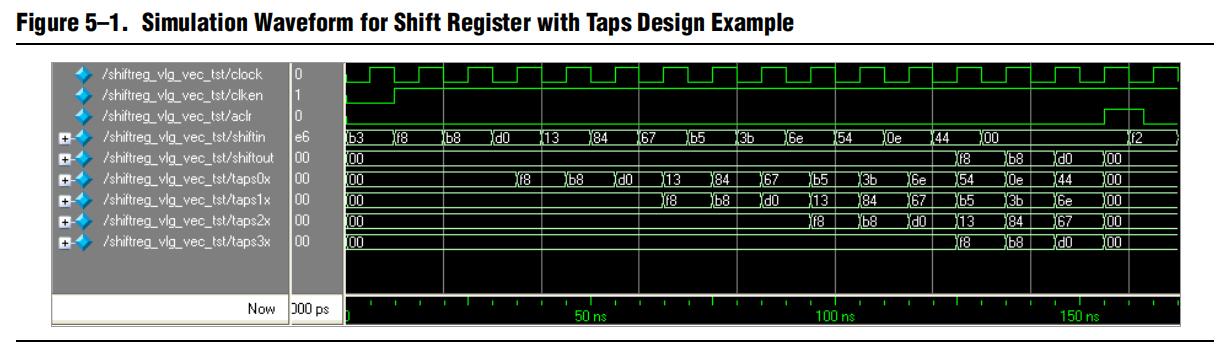
官方解释:“ 这个例子展示的效果为:当全部 12 个数据都移到移位寄存器中时,如何同时使用第 1 - 4 - 7 - 10 个数据(其次是第 2-5-8-11 个和第 3-6-9-12个数据)。”
看到这肯定是一脸懵逼的,完全不知道他表达的什么意思,因此我们还是自己再梳理一下图中的信息:
1、有 12 个数据作为 shift ip 核的输入即 shiftin信号。
2、和 shiftin一起的还有使能信号 clken,clken 和 shiftin是对齐的。
3、出来了 4 串数据。shiftout、taps0x,taps1x,taps2x,taps3x,其中 shiftout 信号和 taps3x信号完全一致。
4、有一个异步清 0 信号aclr,当其拉高有效时,出来的 4 串数据立马为 0。
得到这些信号后稍微清楚了一点,但还是不太理解,那就继续看数据手册:
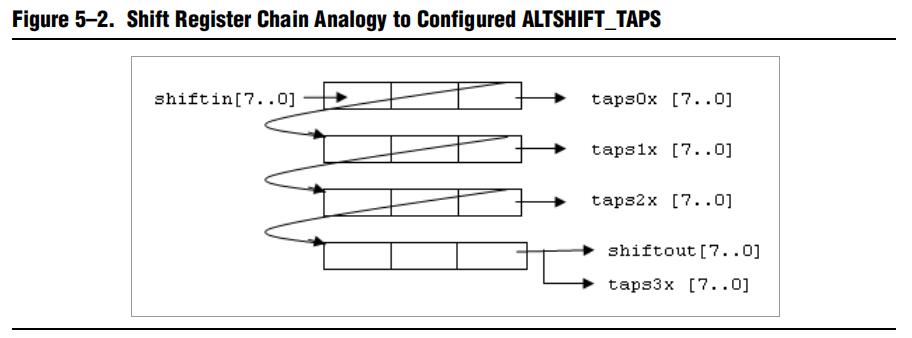
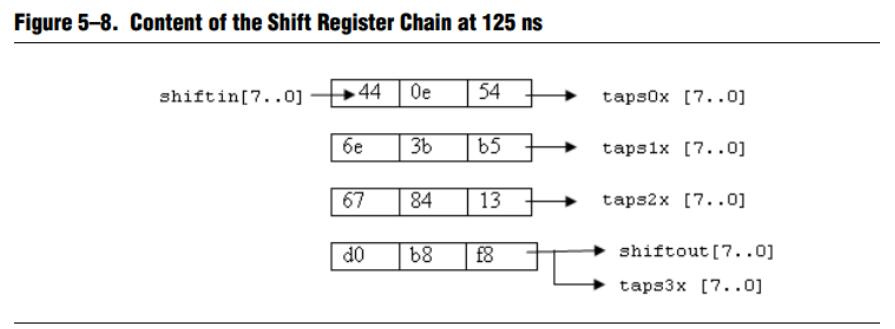
这个示意图解释了 shift ip 核的内部原理。shiftout 信号和 taps3x信号相同。进去 1 串数据就出来平行的 4 串数据,f8 、13、b5、54在时序上是同一时刻出来的,同样的 b8,84,3b,0e是同一时刻出来的,d0,67,6e,44也是同一时刻出来的。由此我们可以看出 shift ip 核很像是一个 RAM,但是这个 RAM 里面有好几道沟槽,当一个沟槽填满后就转移到下一个沟槽,同时每个沟槽都有一个接口引出来,利用这些沟槽的接口就能做很多事情了,例如轻松的实现 3x3、5x5等矩阵。
这个图理解了,但实际运用时还是会迷糊,因为看起来 shiftin 在最上面,而最下面的数据反而是最开始进去的。如果是图片数据,那完全就是倒过来了,此外shiftin的位置也比较模糊,因此我制作一张倒过来的图,方便后面生成 3x3 矩阵时的理解。
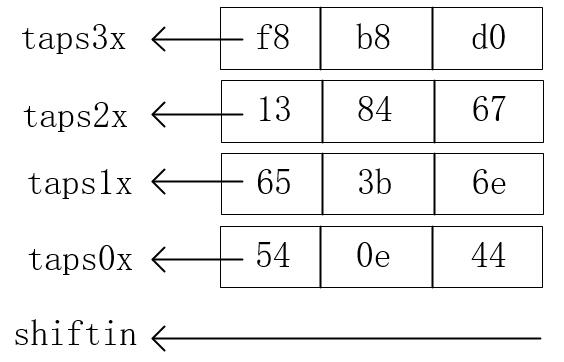
由于 shiftout 和 taps3x 信号是完全相同的,因此没有画出,实际使用时也不需要使用 shiftout 信号。而 shiftin 信号在官方原版图中容易让人误解,正确的位置如图所示。倒过来后就清楚的知道,最先开始的数据在左上角,就像一张图片的第一个像素一样,后面的像素顺序排列,排满一行换下一行,而最下面的信号则是shiftin,即端口中的输入信号。
二、Shift IP 核生成 3x3 矩阵
1、IP核生成
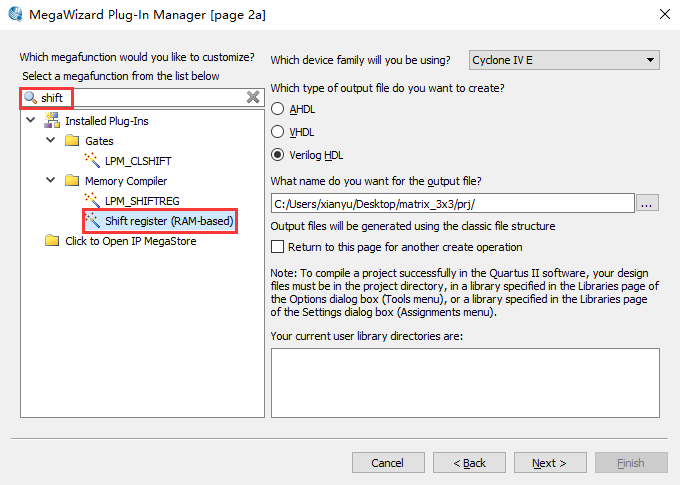
(1)打开 Quartus II 的 IP核生成向导,输入 shift,点击如图所示的 IP核并命名。
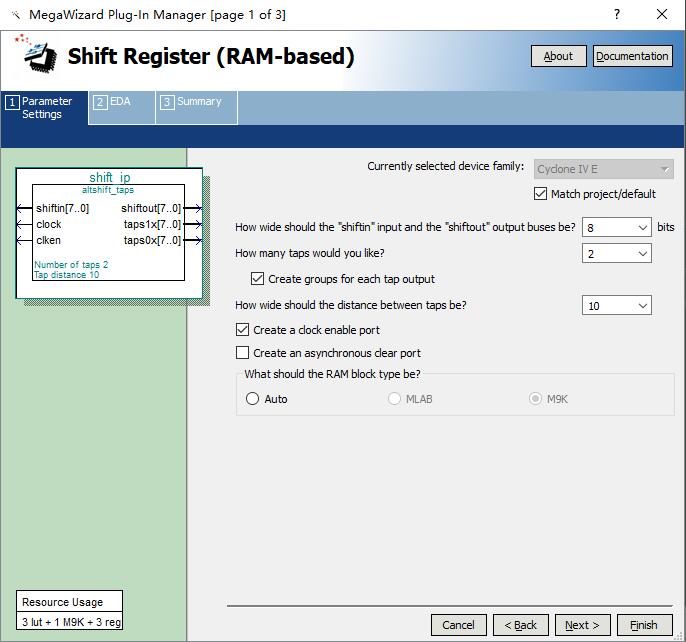
(2)本次设计是仿真 10x5 像素的图片,数据为 8bit,因此位宽选择为8,taps 选择为 2,即 2 个 taps 和 din 就已经满足 3 条平行数据了。默认是未勾选 “taps分组” 选项,这样出来的是一个大 taps,而我们需要的是多个 taps 数据,所以必须勾选上 “taps分组” 选项。taps之间的距离为一行的数据个数 10。再勾选时钟使能接口,这个实际上就是写使能。异步清 0 信号不用勾选,这里用不到。顺便说一下,是没有读使能的,ip核内数据存储到一定数量就会自动吐出。
2、IP核调用
shift_ip u_shift_ip
(
.clken (din_vld ),
.clock (clk ),
.shiftin (din ),
.shiftout ( ),
.taps0x (taps0x ),
.taps1x (taps1x )
);
到这一步实际上相当于完成了之前双 FIFO 法生成 3x3 矩阵的 “IP核调用 + 行列计数规划 + FIFO读写信号设置”,只能说 shift ip 核太适合用来生成矩阵了。
3、生成3x3矩阵
和双 FIFO 的 show-ahead 模式完全一样,就是要注意一下矩阵的数据选取,脑子得转个 180 度的弯来,一旦转过来了就非常简单,没转过来的话就难理解了。
//矩阵数据选取 //--------------------------------------------------- assign row_1 = taps1x; assign row_2 = taps0x; assign row_3 = din; //打拍形成矩阵,矩阵顺序归正 //--------------------------------------------------- always @(posedge clk or negedge rst_n) begin if(!rst_n) begin {matrix_11, matrix_12, matrix_13} <= {8'd0, 8'd0, 8'd0}; {matrix_21, matrix_22, matrix_23} <= {8'd0, 8'd0, 8'd0}; {matrix_31, matrix_32, matrix_33} <= {8'd0, 8'd0, 8'd0}; end else begin {matrix_11, matrix_12, matrix_13} <= {matrix_12, matrix_13, row_1}; {matrix_21, matrix_22, matrix_23} <= {matrix_22, matrix_23, row_2}; {matrix_31, matrix_32, matrix_33} <= {matrix_32, matrix_33, row_3}; end end
三、仿真分析
此次仿真脚本和之前的双 FIFO 是完全一样的,即模拟一张 5x10 分辨率的图片,最终波形如下所示:

波形是对齐了的,还是和双 FIFO 一样再来分析一下换行和换帧的情况吧。
1、换行数据的问题
取第4行数据的第一个矩阵来看,其数据为{11,11,11,21,21,21,30,30,31},数据主要是复制了本矩阵的最后一列,即图像数据的第一列。此外还借用了 2 次上一行最后一个矩阵的 1 个数据。和 show-ahead 模式的双FIFO法是一模一样的情况。
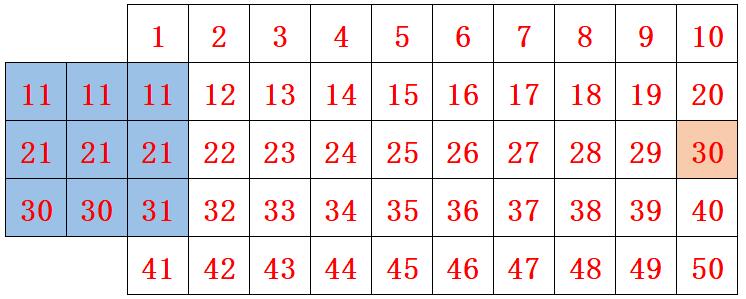
实验推理:图像最左边出现一个不怎么违和的竖条,隐隐约约像是第一列的复制。
2、换帧数据的问题
换帧后一开始的矩阵为{31,31,31,41,41,41,50,50,1},借用了上一帧图片末尾的数据。 整个第一排矩阵的数据都是借用了上一帧图片末尾的最后两行数据。
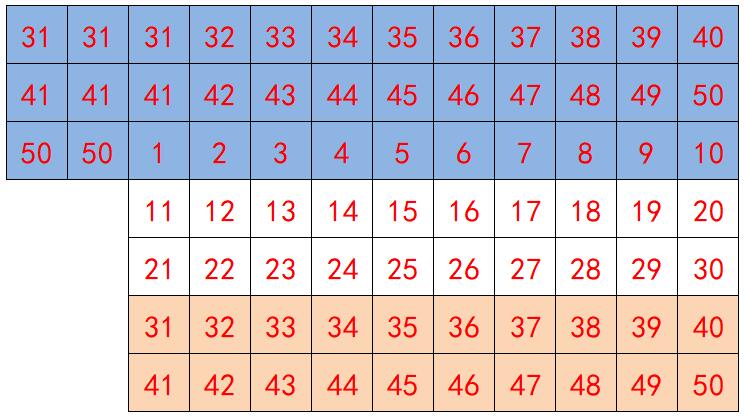
实验推理:最上边出现一个违和的横条,隐隐约约像是图片最下边的图形。
四、实际上板
这次选择一张最下边有一些白点的图片,以均值滤波的实现来测试这次的 3x3 矩阵效果。关于均值滤波后面会单独拿出来讲解。原图如下:

经过处理后得到如下图片:

隐约看到最左边有一条模糊的线,但不怎么违和。而最上边出现了一些白色线段,刚好对应了最下方的那些白点。实验最终和我们的推理一致。
五、后记
shift ip 核生成 3x3 矩阵比双 FIFO 简单太多了,代码量极少。但是它也有局限性,如果要改进为边界补 0 或边界复制的话还不如就用 双FIFO 来实现。但 shift ip 核胜就胜在简洁,而且我们做图像处理时不会在乎边界的那一丁点问题,重点还是关注图像处理算法本身以及最后实现的图像整体效果。
在 ISE 和 Vivado 中其实也有 shift ip 核,和本篇博客略有差异。关于生成 3x3 矩阵的方法就整理到这,足够用了。
参考资料:
[1]CrazyBingo 图像处理教程
[2]NingHechuan 图像处理教程