选择排序(C++，Java，Python实现）

排序算法之选择排序,选择排序，选择排序的基本思想描述为：每一趟在n-i+1(i=1,2,…,n-1)个记录中选取关键字最小的记录作为有序序列中第i个记录。具体来说，假设长度为n的数组arr，要按照从小到大排序，那么先从n个数字中找到最小值min1，如果最小值min1的位置不在数组的最左端(也就是min1不等于arr[0])，则将最小值min1和arr[0]交换，接着在剩下的n-1个数字中找到最小值min2，如果最小值min2不等于arr[1]，则交换这两个数字，依次类推，直到数组arr有序排列。

算法过程

举个栗子（第一趟的排序过程）

原始序列：3、44、38、5、47、15、36、 26、27、2、46、4、19、50、48

1）在进行选择排序过程中分成有序和无序两个部分，开始都是无序序列

结果：3、44、38、5、47、15、36、 26、27、2、46、4、19、50、48

2）从无序序列中取出最小的元素2，将2同无序序列第一个元素交换，此时产生仅含一个元素的有序序列，无序序列减一

结果：{2、} {44、38、5、47、15、36、 26、27、3、46、4、19、50、48

3）从无序序列中取出最小的元素3，将3同无序序列第一个元素交换，此时产生仅两个元素的有序序列，无序序列减一

结果：{2、3、} {38、5、47、15、36、 26、27、44、46、4、19、50、48}

4）从无序序列中取出最小的元素4，将4同无序序列第一个元素交换，此时产生含三个元素的有序序列，无序序列减一

结果：{2、3、4、} {5、47、15、36、 26、27、44、46、38、19、50、48}

5）从无序序列中取出最小的元素5，5此时是无序序列最小的，不用交换

结果：{2、3、4、5、} {47、15、36、 26、27、44、46、38、19、50、48}

6）从无序序列中取出最小的元素15，将15同无序序列第一个元素交换，此时产生含五个元素的有序序列，无序序列减一

结果：{2、3、4、5、15、} {47、36、 26、27、44、46、38、19、50、48}

7）依次重复上述操作，直到无序序列只有最后一个元素

8）最后一个元素50肯定是最大元素，无序排序直接生产一个有序的序列

结果：{2、3、4、5、19、26、27、36、38、44、46、47、48、50}

最后如果还没有理解这个过程的话，小编放上一个动图，让大家更深入的理解这个过程：

接下来分析完了插入排序的算法，我们就到了分享代码的这个激动人心的时刻了：

插入排序C++实现代码：

#include <iostream>
using namespace std;
#include <vector>
#include <time.h>
vector<int> get_random(int n, int N);
const int MAX_NUM=10000;
int data[100];//定义一个产生数组储存100个随机数
void SelectSort(int n);//选择排序
void output(int n);
void Swap(int i,int j);
int main() 
{
  srand((unsigned int)time(0));
  vector<int> randsample=get_random(100,MAX_NUM);//产生100个0-MAZX_NUM的随机数,每次产生的随机数不一样
  int size=randsample.size();
  //输出最开始时未排序时的顺序:
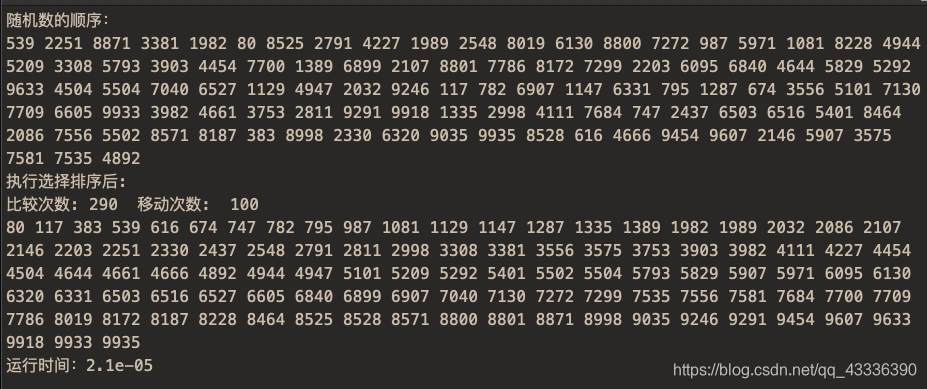
  cout<<"随机数的顺序："<<endl;
  for(int i=0;i<randsample.size();i++)
  {
    cout<<randsample[i]<<" ";
  }
  cout<<endl;
  clock_t start,finish;//定义一个测量一段程序运行时间的前后值
  double totaltime;//总的运行时间
  
  //测试选择排序
  cout<<"执行选择排序后:"<<endl;
  for(int i=0;i<randsample.size();i++)
  {
    data[i]=randsample[i];
  }
  start=clock();
  SelectSort(size);
  finish=clock();
  output(size);
  totaltime=(double)(finish-start)/CLOCKS_PER_SEC;
  cout<<"运行时间："<<totaltime<<endl;
}
//产生随机数的函数
vector<int> get_random(int n, int N)
{
  vector<int> vec(N);//N代表初始状态分配的空间大小
  vector<int> out_vec;
  for(int i=0;i<N;++i)
  {
    vec[i]=i;
  }
  for (int i=0;i<n;++i)
  {
    int rand_value=rand()%N;
    out_vec.push_back(vec[rand_value]);
    vec[rand_value]=vec[N-1];//将数组vec的元素
    N--;
  }
  return out_vec;
}
//直接选择排序
void SelectSort(int n)
{
  int i,j;
  int count=0;
  int count1=0;
  for(i=0;i<n;i++)
  {
    int k=i;//在data[i]到data[n-1]找最小排序码元素
    for(j=i+1;j<n;j++){
      if(data[j]<data[k]){
        count++;//当前具有最小排序码的元素
        k=j;
      }
    }
    if(k!=i)
    Swap(i,k);//交换
    count1++;
  }
  cout<<"比较次数: "<<count<<"  移动次数:  "<<count1<<endl;
}
void output(int n)
{
  for(int i=0;i<n;i++)
  {
    cout<<data[i]<<" ";
  }
  cout<<endl;
}
//交换函数
void Swap(int i,int j)
{
  int tem;
  tem = data[j];
  data[j]= data[i];
  data[i] = tem;
}
  

插入排序Java代码实现

import java.util.ArrayList;
import java.util.List;
import java.util.Random;

public class SelectSort
{
  public static void main(String[] args)
  {
    Object []arr = getRandomNumList(100,0,10000).toArray();
    int[] ins = new int [100] ;
    System.out.println("排序前：");
    for(int i = 0; i < arr.length; i++) {
      String s=arr[i].toString();
      ins[i]= Integer.parseInt( s );
      System.out.println(ins[i]);
      }
    System.out.println("排序后：");
    int[] ins2 = selectsort(ins);
    for(int i = 0; i < arr.length; i++) {
      System.out.println(ins2[i]);
      }
  }
  
  public static int[] selectsort(int[] data){
    int i,j;
    int n = data.length-1;
    for(i=0;i<n;i++)
    {
      int k=i;//在data[i]到data[n-1]找最小排序码元素
      for(j=i+1;j<n;j++){
        if(data[j]<data[k]){//当前具有最小排序码的元素
          k=j;
        }
      }
      if(k!=i)
      {
        int tem;
        tem=data[k];
        data[k]=data[i];
        data[i]=tem;
      }
    }
    return data;
  }
   //定义生成随机数并且装入集合容器的方法
    //方法的形参列表分别为：生成随机数的个数、生成随机数的值的范围最小值为start(包含start)、值得范围最大值为end(不包含end)  可取值范围可表示为[start,end)
    public static List getRandomNumList(int nums,int start,int end){
        //1.创建集合容器对象
        List list = new ArrayList();

        //2.创建Random对象
        Random r = new Random();
        //循环将得到的随机数进行判断，如果随机数不存在于集合中，则将随机数放入集合中，如果存在，则将随机数丢弃不做操作，进行下一次循环，直到集合长度等于nums
        while(list.size() != nums){
            int num = r.nextInt(end-start) + start;
            if(!list.contains(num)){
                list.add(num);
            }
        }
        return list;
    }
}

插入排序Python代码实现

import random
def sort(arr):
    for j in range(len(arr)-1):
        minIndex = j
        for i in range(j+1,len(arr),1):
            if(arr[i] < arr[minIndex]):
                minIndex = i
        arr[j],arr[minIndex] = arr[minIndex],arr[j]

def main():

    arr =[]
    while(len(arr)<100):
        x=random.randint(0,10000)
        if x not in arr:
            arr.append(x)
    sort(arr)
    print(arr)

if __name__ == "__main__":
    main()

算法分析：

直接选择排序的排序码比较次数KCN与元素的初始排列无关。第i趟选择具有最小排序码元素所需的比较次数总是n-i-1次，此处假定整个待排序元素序列有n个元素。因此，总的排序码比较次数为:

$displaystyle KCN=sum_{i=0}^{n-2}{(n-i-1)}$=n*(n-1)/2

元素的移动次数与元素序列的初始排列有关。当这组元素的初始状态是按其排序码从小到大有序的时候，元素的移动次数RMN=0，达到最少；而最坏情况是每一趟都要进行交换，总的元素移动次数为RMN=3（n一1)。它对一类重要的元素序列具有较好的效率，这就是元素规模很大，而排序码却比较小的序列。因为对这种的序列进行排序，移动操作所花费的时间要比比较操作的时间大得多，而其他算法移动操作所花费的时间要比比较操作的时间大的多，而其他算法移动操作次数都要比选择排序来得多。直接选择排序是一种不稳定的排序方法。

以上就是本次给大家分享的选择排序的几种实现,如果有什么不足之处欢迎大家指出，留言，互相学习，共同进步。花了几个小时整理，希望得到大家的支持,你的支持就是我前进的动力,下面我会持续更新其他的排序算法，敬请期待！想要了解其他相关内容也可以访问我的个人博客相逢的博客（里面有hexo搭建博客等相关内容）