排序算法之冒泡排序,冒泡排序,冒泡排序是一种简单的排序算法。它重复地走访过要排序的数列,一次比较两个元素,如果它们的顺序错误就把它们交换过来。走访数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。
算法描述:
起泡排序的基本方法是:设待排序元素序列中的元素个数为n,首先比较第n-2个元素和第n-1个元素,如果发生逆序,即前一个大于后一个),则将这两个元素交换;然后对第n-3个和第n-2个元素(可能是刚交换过来的)做同样处理;重复此过程直到处理完第0个和第1个元素。我们称它为一趟起泡,结果将最小的元素交换到待排序元素序列的第一个位置,其他元素也都向排序的最终位置移动。当然在个别情形下,元素有可能在排序中途向相反的方向移动,但元素移动的总趋势是向最终位置移动。正因为每一趟起泡就把一个排序码小的元素前移到它最后应在的位置,所以叫做起泡排序。这样最多做n一1趟起泡就能把所有元素排好序。
算法过程:
原始序列:3、44、38、5、47、15、36、 26、27、2、46、4、19、50、48
我们需要 拿第一个和第二个对比 如果第一个比第二个大那么就换位置,如果小就不换,接下来拿第二个和第三个…这样依次下去比到最后 我们把这些数中最大的一个放在了右边, 然后再重复以上的方式下去就这些数只第二个大的放在了倒数第二位,依次下去…
1、比较相邻的元素。如果第一个比第二个大(小),就交换他们两个。
2、对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。这步做完后,最后的元素会是最大(小)的数。
3、针对所有的元素重复以上的步骤,除了最后已经选出的元素(有序)。
4、持续每次对越来越少的元素(无序元素)重复上面的步骤,直到没有任何一对数字需要比较,则序列最终有序。
结果:{2、3、4、5、19、26、27、36、38、44、46、47、48、50}
冒泡排序个人认为是最简单的一个排序,也挺容易记住的,过程中会发生大量的交换,就没有像选择排序那样写步骤,如果大家还没有理解这个过程的话,小编依旧放上一个动图,让大家更深入的理解这个过程:
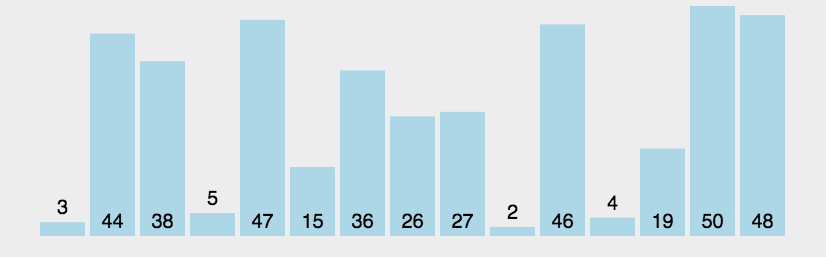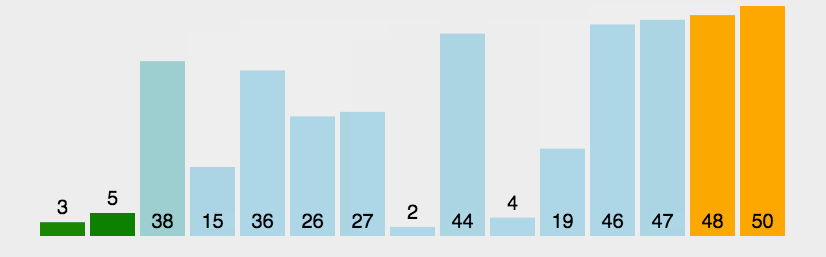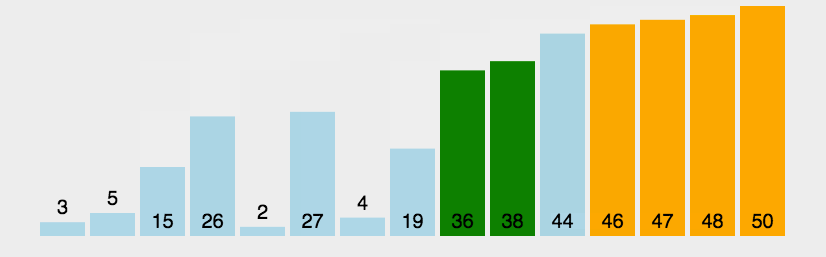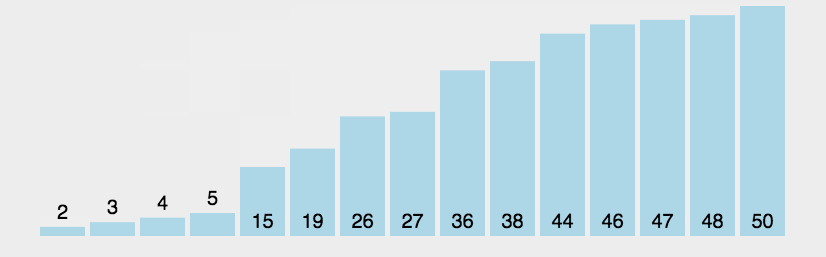
{% endnote %}
冒泡排序的C++,Java,Python实现
因为小编也是java,python的初学者,写的不好的地方请大家见谅,后面的各大算法都会加入一个随机数的产生,基本上的实现大致相同,除了排序算法会变之外
冒泡排序C++实现代码:
#include <iostream>
using namespace std;
#include <vector>
#include <time.h>
vector<int> get_random(int n, int N);
const int MAX_NUM=10000;
int data[100];//定义一个产生数组储存100个随机数
void ExchangeSort(int n);//冒泡排序
void output(int n);
void Swap(int i,int j);
int main()
{
srand((unsigned int)time(0));
vector<int> randsample=get_random(100,MAX_NUM);//产生100个0-MAZX_NUM的随机数,每次产生的随机数不一样
int size=randsample.size();
//输出最开始时未排序时的顺序:
cout<<"随机数的顺序:"<<endl;
for(int i=0;i<randsample.size();i++)
{
cout<<randsample[i]<<" ";
}
cout<<endl;
clock_t start,finish;//定义一个测量一段程序运行时间的前后值
double totaltime;//总的运行时间
//测试冒泡排序
cout<<"执行选择排序后:"<<endl;
for(int i=0;i<randsample.size();i++)
{
data[i]=randsample[i];
}
start=clock();
ExchangeSort(size);
finish=clock();
output(size);
totaltime=(double)(finish-start)/CLOCKS_PER_SEC;
cout<<"运行时间:"<<totaltime<<endl;
}
//产生随机数的函数
vector<int> get_random(int n, int N)
{
vector<int> vec(N);//N代表初始状态分配的空间大小
vector<int> out_vec;
for(int i=0;i<N;++i)
{
vec[i]=i;
}
for (int i=0;i<n;++i)
{
int rand_value=rand()%N;
out_vec.push_back(vec[rand_value]);
vec[rand_value]=vec[N-1];//将数组vec的元素
N--;
}
return out_vec;
}
//冒泡排序,又称选择排序,加入一个exchange来改进排序时间
void ExchangeSort(int n)
{
int count=0;
int count1=0;//count,count1分别用来计算比较次数和移动次数
int tem;
bool exchange;
for(int i=0;i<n-1;i++){
exchange=false;//检查前假设没有发生排序
for(int j=i+1;j<n;j++){
if(data[i]>data[j]){
count++;
Swap(i, j);
count1++;
exchange=true;
}
}
if(exchange==false)
{
count++;
return;
}
}
cout<<"比较次数: "<<count<<" 移动次数: "<<count1<<endl;
}
void output(int n)
{
for(int i=0;i<n;i++)
{
cout<<data[i]<<" ";
}
cout<<endl;
}
//交换函数
void Swap(int i,int j)
{
int tem;
tem = data[j];
data[j]= data[i];
data[i] = tem;
}
测试结果
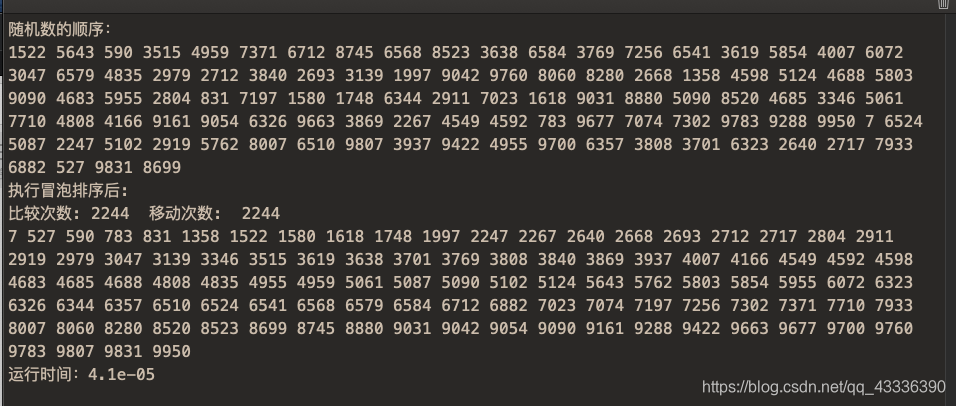
排序Java代码实现
import java.util.ArrayList;
import java.util.List;
import java.util.Random;
public class ExchangeSort
{
public static void main(String[] args)
{
Object []arr = getRandomNumList(100,0,10000).toArray();
int[] ins = new int [100] ;
System.out.println("排序前:");
for(int i = 0; i < arr.length; i++) {
String s=arr[i].toString();
ins[i]= Integer.parseInt( s );
System.out.println(ins[i]);
}
System.out.println("排序后:");
int[] ins2 = exchangesort(ins);
for(int i = 0; i < arr.length; i++) {
System.out.println(ins2[i]);
}
}
public static int[] exchangesort(int[] data){
int exchange;
int n = data.length-1;
for(int i=0;i<n-1;i++){
exchange=0;//检查前假设没有发生排序
for(int j=i+1;j<n;j++){
if(data[i]>data[j]){
int temp;
temp = data[j];
data[j]= data[i];
data[i] = temp;
exchange=1;
}
}
if(exchange==0)
{ }
}
return data;
}
//定义生成随机数并且装入集合容器的方法
//方法的形参列表分别为:生成随机数的个数、生成随机数的值的范围最小值为start(包含start)、值得范围最大值为end(不包含end) 可取值范围可表示为[start,end)
public static List getRandomNumList(int nums,int start,int end){
//1.创建集合容器对象
List list = new ArrayList();
//2.创建Random对象
Random r = new Random();
//循环将得到的随机数进行判断,如果随机数不存在于集合中,则将随机数放入集合中,如果存在,则将随机数丢弃不做操作,进行下一次循环,直到集合长度等于nums
while(list.size() != nums){
int num = r.nextInt(end-start) + start;
if(!list.contains(num)){
list.add(num);
}
}
return list;
}
}
冒泡排序Python代码实现
import random
def ExchangeSort(nums):
for i in range(len(nums) - 1):
ex_flag = False # 改进后的冒泡,设置一个交换标志位
for j in range(len(nums) - i - 1):
if nums[j] > nums[j + 1]:
nums[j], nums[j + 1] = nums[j + 1], nums[j]
ex_flag = True
if not ex_flag:
return nums # 这里代表计算机偷懒成功 (〃'▽'〃)
return nums # ExchangeSort这里代表计算机没有偷懒成功 o(╥﹏╥)o
def main():
arr =[]
while(len(arr)<100):
x=random.randint(0,10000)
if x not in arr:
arr.append(x)
ExchangeSort(arr)
print(arr)
if __name__ == "__main__":
main()
算法分析:
起泡排序中,第i趟起泡中需要执行n一i次比较和交换操作。因此,从1到n一1,执行行的比较操作的次数为:
(n-1)+(n-2)+…+2+1=n(n-1)/2
从排序的执行过程中可以看到基本的起泡排序的数据比较次数与输人序列中各待排序元素的初始排列无关,但数据的交换次数与各待排序元素的初始排列有关,它与逆序的发生有关,最好情况下可能一次也不交换,最差情况下每一次比较都需要交换。
为此,在算法中可增加一个标志exchange,用以标识本趟起泡结果是否发生了逆序和交换。如果没有发生交换则exchange=false,表示全部元素已经排好序,因而可以停止处理,结束算法;如果xchange=true,表示本趟有元素发生交换,还需执行下一趟排序。
在做了这样的改进之后,如果元素序列已经有序,那么只需要一趟起泡,算法就顺利结束了。因此,对于改进的起泡算法,最好的情况下需要n次比较和0次交换操作,而在一般情况最差情况下,排序算法大约需要/2次比较和交换操作.
以上就是本次给大家分享的冒泡排序的几种语言的实现,如果有什么不足之处欢迎大家指出,留言,互相学习,共同进步。希望得到大家的支持,你的支持就是我前进的动力,接下来我会持续更新其他的排序算法,敬请期待!