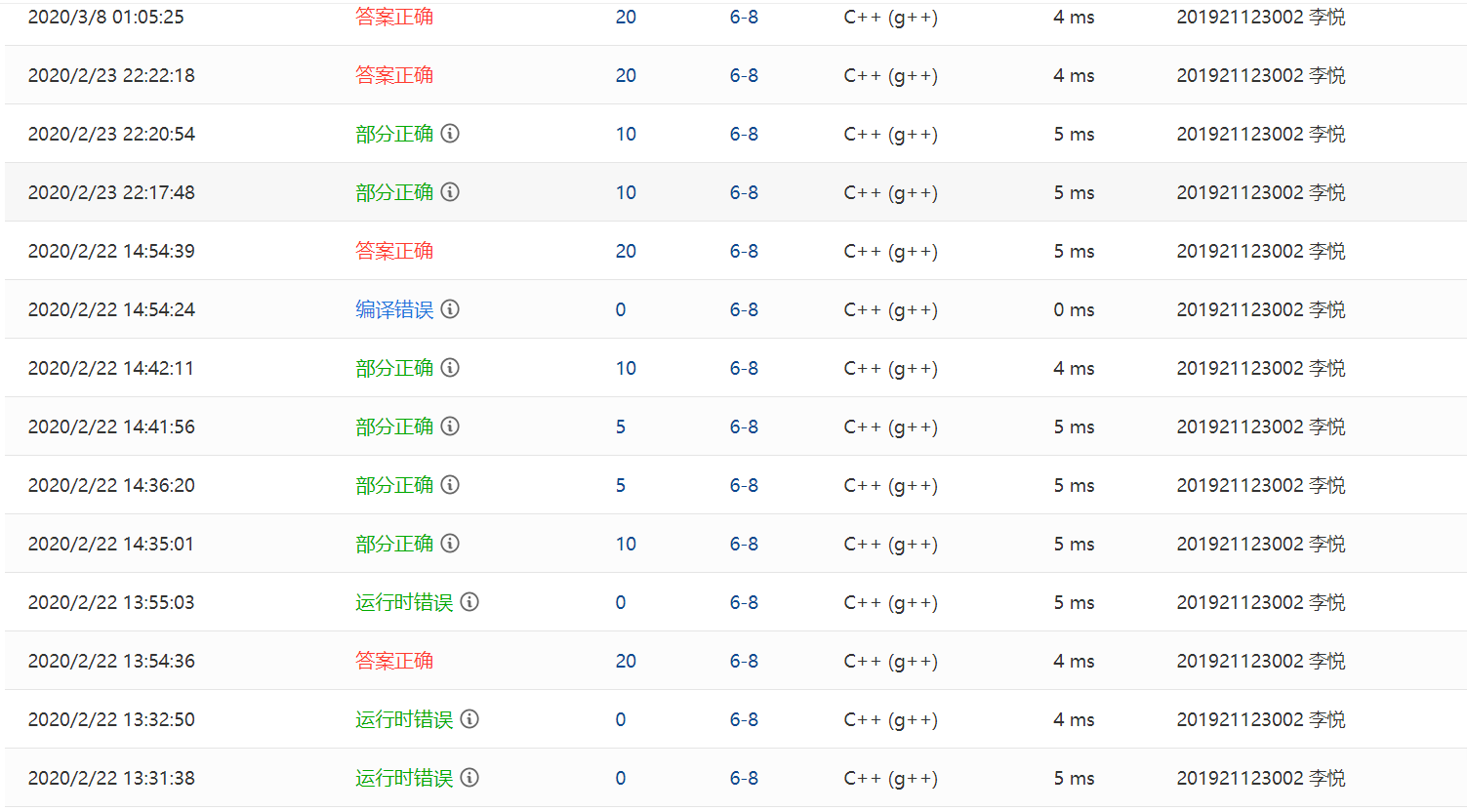
0.PTA得分截图

1.1 线性表学习总结

1.线性表的基本概念
线性表是一个具有n个相同特性的有限序列,所有元素都属于同一种数据类型。线性表的逻辑结构简单,便于实现和操作,运用范围广泛。按照存储方式可以分为:顺序表和链表。
2.顺序表
将数据依次存储在连续的整块物理空间中,各结点间的存储单元地址是连续的。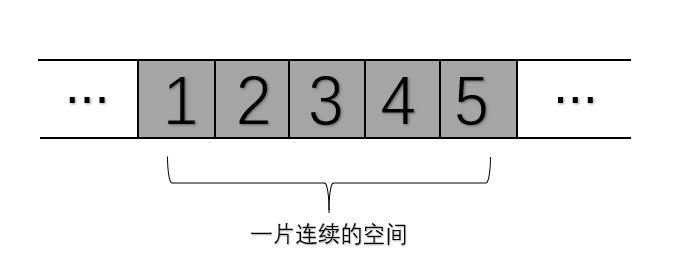
结构体定义
typedef struct node{
ElemType data[MAX];
int length;//保存线性表的长度,或者也可以定义int型变量last用于保存线性表中最后一个数据所在的位置下标。
}Node,*NodeList;
基本操作
-
顺序表的插入:实质上就是移动数组的操作,可以从头开始遍历,找到插入的位置后,开始移动数组,或者从末尾开始边移动数组边比较,找到插入的位置后,直接插入;
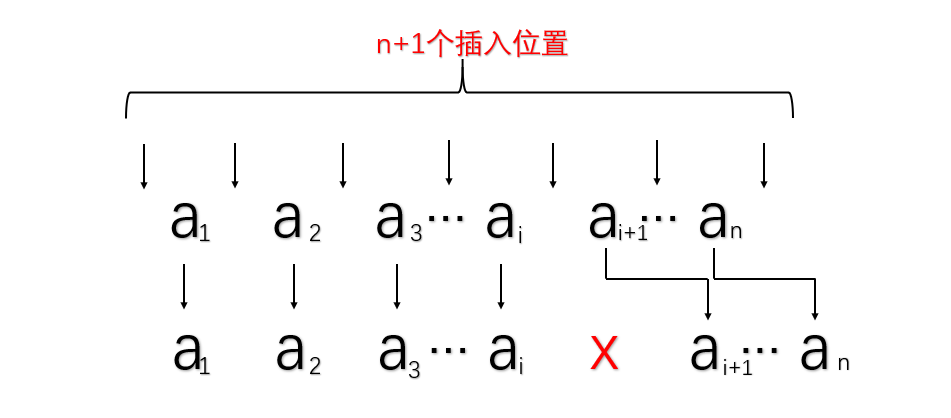
- 伪代码:
void InserList(NODE & list,int x)
{
判断顺序表是否满了,如果满了就return
for i=list.length to 0 //从末尾开始一个一个把数据右移,直到找到x的插入位置停止。
if x>list.data[i-1] //找到插入位置,退出循环;
break;
else
list.data[i]=list.data[i-1];//数据进行右移;
end if
end for
list.length++;//一定要记得修改顺序表的长度!
list.data[i]=x;//插入数据;
}
-
具体代码及实现结果:

-
顺序表的删除:实质上也是移动数组中的数据,一般使用的是重构顺序表的方法。
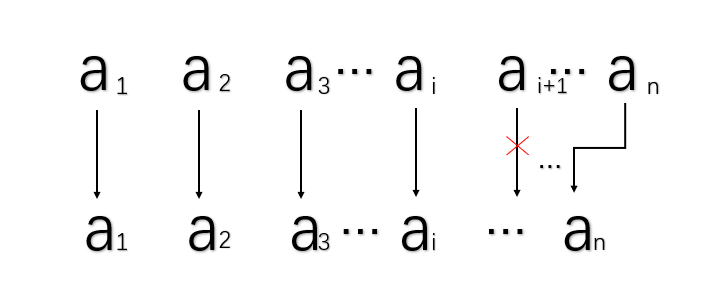
- 伪代码:
void DeleteData(NODE &list, int x)
{
定义变量i来遍历顺序表;
定义变量j并初始化为0;
定义变量flag用于判断删除是否成功,初始化为0;
for i=0 to list.length
if(list.data[i]!=x)//不是删除的数据x就存入顺序表中;
list.data[j++]=list.data[i];
else
flag=1;
end if
end for
list.length=j;
判断是否删除成功。
}
- 具体代码实现及结果:

3.单链表
数据分散存储在物理空间中,各结点间的存储单元的地址不一定连续,为表示其逻辑关系,增加了指针next,通过指针建立起一条链来保存数据。
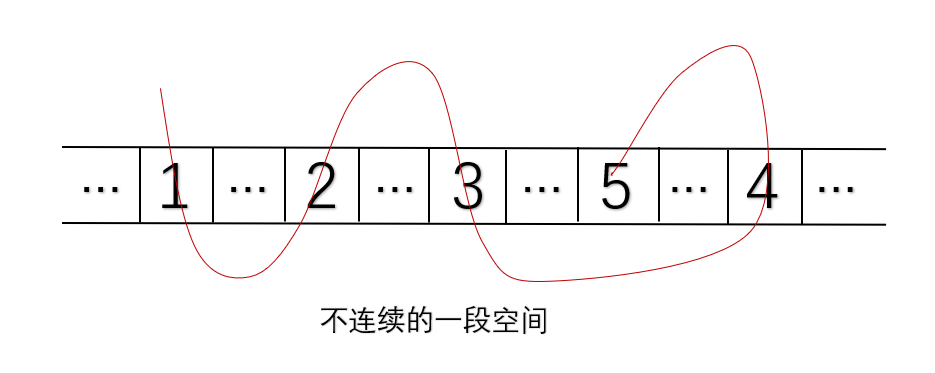
结构体定义
typedef struct node
{
Elemtype data;
struct node* next;
}Node,*ListNode;
基本操作
- 头插法创建单链表:链表结点次序于逻辑次序相反。
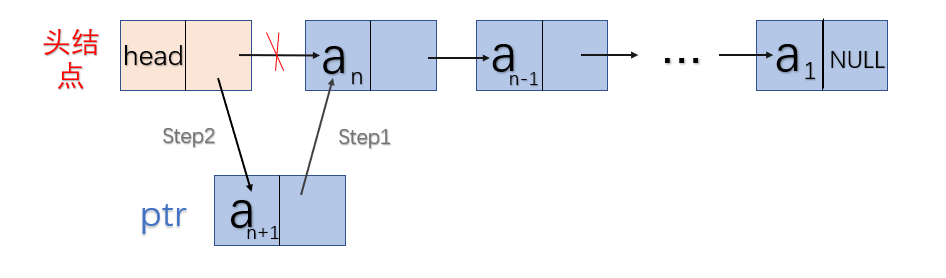
- 伪代码:
void GreatList(ListNode&head,int n)
{
head=new Node;//为list申请空间;
head->next=NULL;
定义结构体指针ptr来保存每一个结点;
for i=0 to n
ptr=new Node;//为ptr申请空间;
输入数据赋给ptr->data;
ptr->next保存头结点head的下一个结点;
head->next保存ptr;
end for
}
-
具体代码及实现结果:
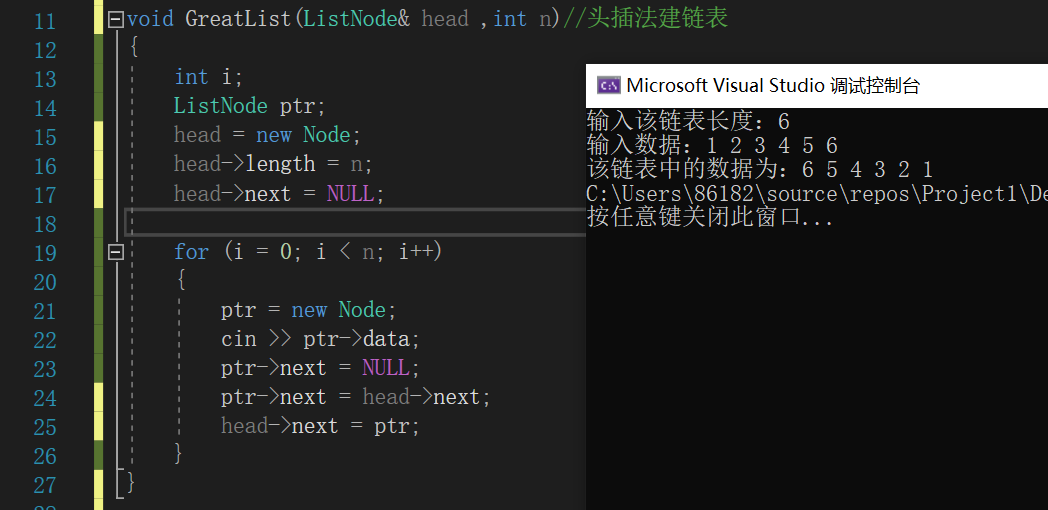
-
尾插法建链表:链表的结点次序和逻辑次序相同。
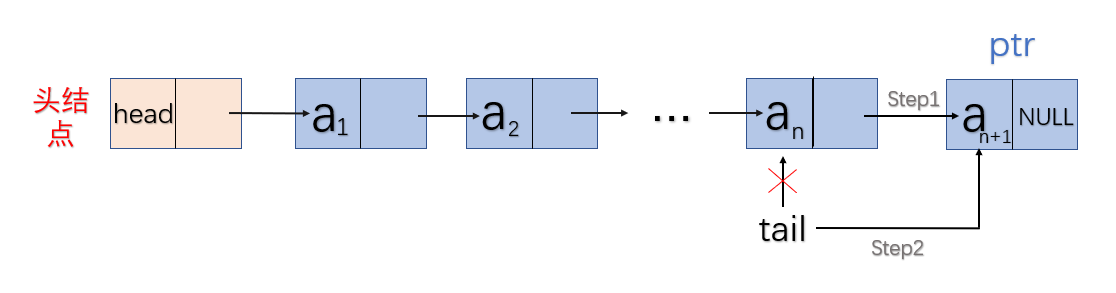
- 伪代码:
void GreatList(ListNode& head,int n)//尾插法
{
定义结构体指针ptr保存每个结点;
定义结构体指针tail指向链表尾部;
/*初始化链表*/
head=new Node;
head->next=NULL;
tail=head;//尾指针先指向头结点;
for i=0 to n
ptr = new Node;
输入数据赋给ptr->data;
ptr->next=NULL;
tail->next=ptr;//先连接;
tail=ptr;//再移动tail;
end for
}
-
具体代码及实现结果:
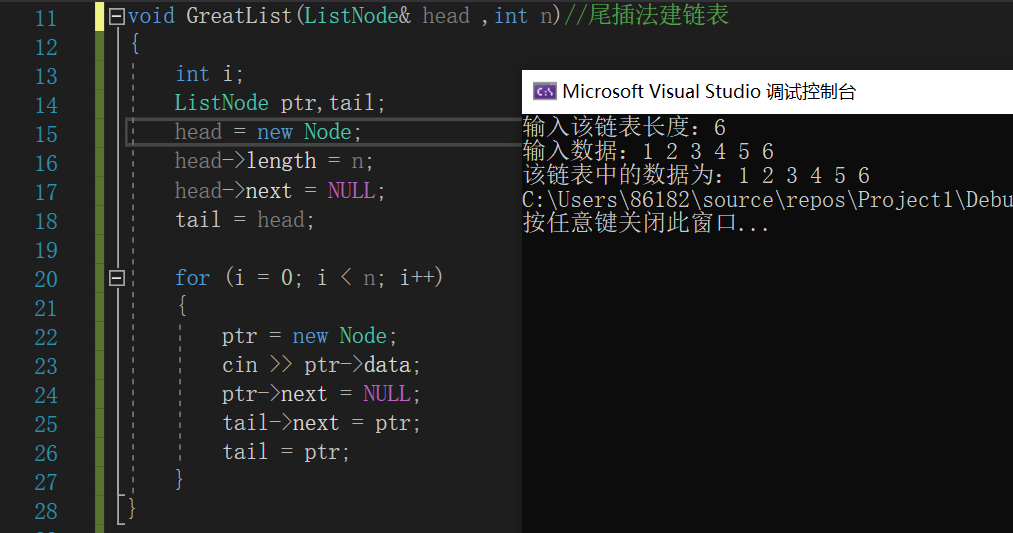
-
链表插入
在插入数据时,当我们找到插入位置时,我们需要修改该位置的前驱指针和后继指针,这时我们需要定义一个前驱指针pre来保存该插入位置的前驱;这样方便我们修改
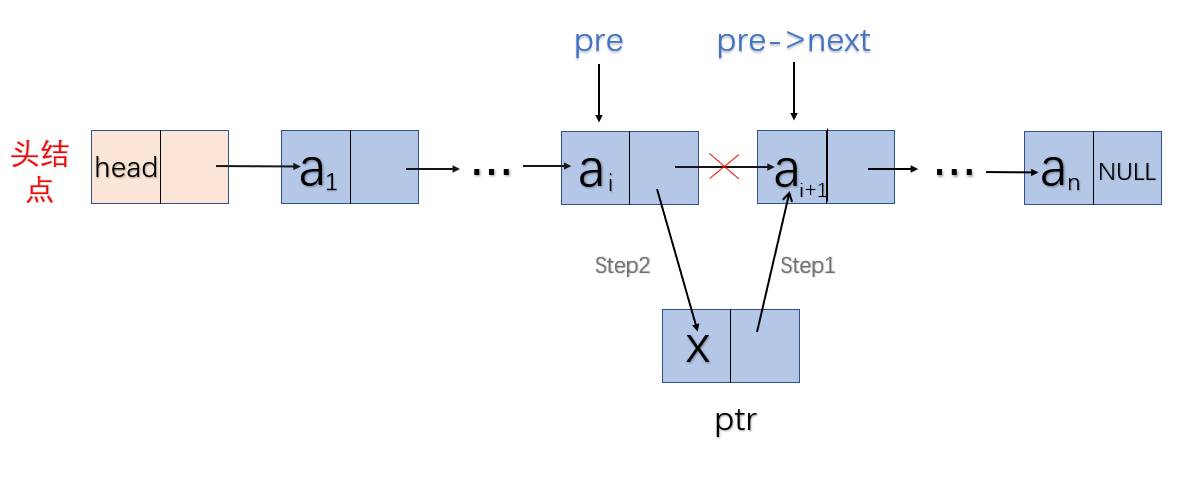
- 伪代码:
void InserData(ListNode& list)
{
定义结构体指针pre用来保存前驱指针;
定义结构体指针ptr保存插入的数据;
初始化ptr;
输入数据赋给ptr;
while(pre->next && 未满足插入条件)
pre = pre->next;
end while
ptr->next=pre->next;//先保存后继指针;
pre->next=ptr;//再修改前驱指针;
}
-
具体代码及实现结果:

-
链表删除
和链表插入一样,也是需要修改删除位置的前驱和后继,所以这里也要设置一个前驱指pre正来保存前驱。

- 伪代码:
void DeletData(ListNode& list)
{
定义结构体指针pre保存删除位置的前驱;
定义结构体指针ptr保存删除的结点;
输入需要删除的数据赋给x;
while(pre->next && 未找到删除的数据)
pre=pre->next;
end while
if pre->next == NULL //说明没有找到删除的数据
输出删除失败;
else //找到了删除的数据;
ptr=pre->next;//ptr保存需要删除的结点;
pre->next=ptr->next;//连接删除结点的前驱和后继;
end if
}
-
具体代码及实现结果:

-
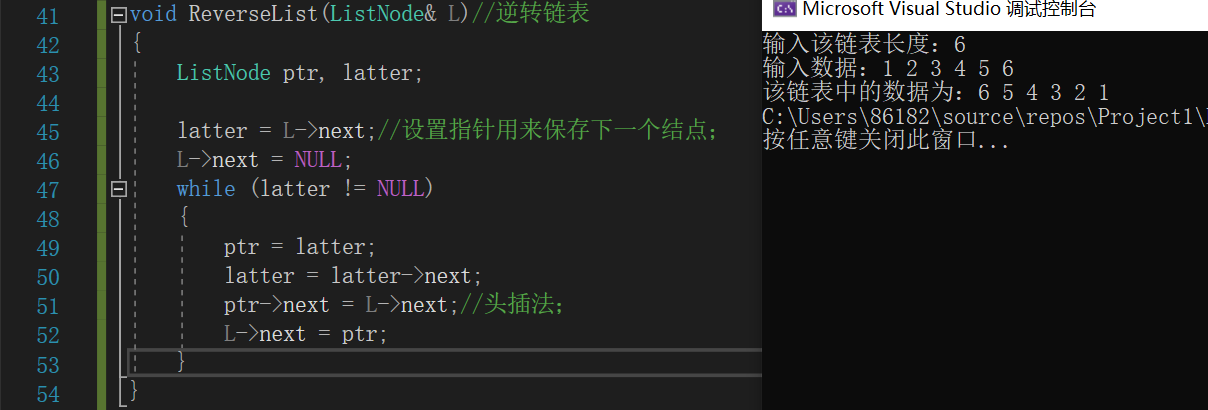
逆转单链表
将一个带头结点的单链表逆转,实质是上是头插法的运用,可直接在原单链表上进行修改,这里需要一个后继指针latter来保存后面未修改的数据;

- 伪代码:
void ReverseList(ListNode& L)
{
定义结构体指针ptr保存当前结点;
定义结构体指针latter保存原链表中ptr的后继结点;
latter=L->next;
L->next=NULL;//重构链表;
while(latter!=NULL)//遍历原链表;
ptr=latter;
latter=latter->next;//保存ptr的后继结点;
/*头插法*/
ptr->next=L->next;
L->next=ptr;
end while
}
-
具体代码及实现结果:
-
链表分割:实质是删除结点和头插法的应用。
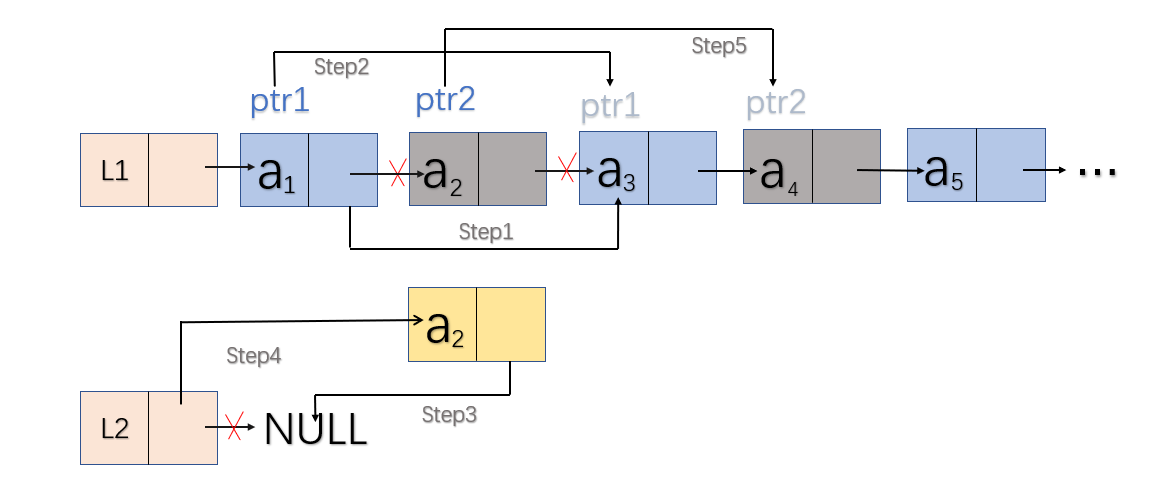
- 伪代码:
void SplitList(ListNode& L, ListNode& L1, ListNode& L2)
{
定义结构体指针ptr1来遍历链表L1;
定义结构体指针ptr2来保存属于链表L2的结点;
/*初始化链表L2*/
L2-next=NULL;
L1=L;//L1和L共享结点;
ptr1=L1->next;
while(ptr1!=NULL && ptr1->next!=NULL)//判断是否遍历结束
ptr2=ptr1->next;//ptr2保存要插入L2的结点;
/*L1做删除结点操作*/
ptr1->next=ptr2->next;
ptr1=ptr2->next;
/*ptr2保存的结点用头插法编入L2中*/
ptr2->next=L2->next;
L2->next=ptr2;
end while
}
- 具体操作及实现结果:

4.有序表
是一种特殊线性表,所有元素以递增或递减的方式有序排列。
基本操作
- 创建有序链表:用结构体指针ptr先保存用户输入的数,然后遍历链表找到可插入的位置。
- 伪代码:
void SortList(ListNode& list,int n)
{
定义结构体指针ptr保存新结点;
定义结构体指针listPtr遍历链表list;
/*初始化链表list*/
list = new Node;
list->next=NULL;
for i=0 to n
ptr=new Node;
输入数据赋给ptr->data;
listPtr=list;//开始遍历链表list;
while(listPtr->next && 未找到插入位置)
listPtr = listPtr->next;
end while
ptr->next=list->next;//开始进行插入;
listPtr->next=ptr;
end for
}
-
具体代码及实现结果:

-
有序单链表的插入:参见上面单链表的插入
-
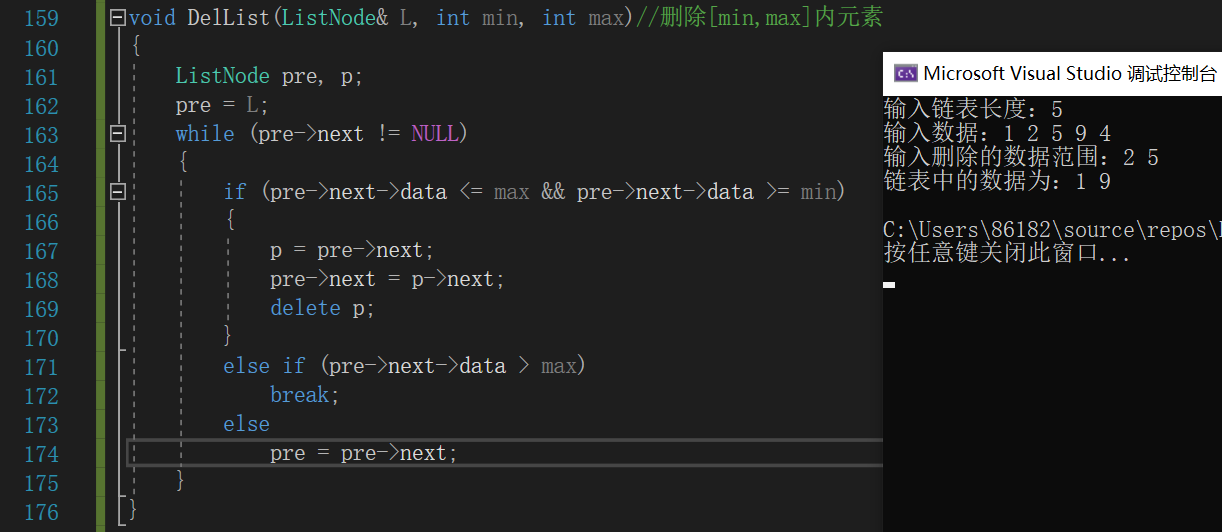
有序单链表删除数据——删除区间数据
6-3 jmu-ds-链表区间删除- 伪代码:
void DelList(ListNode& L, int min, int max)
{
定义结构体指针pre,用pre->next来遍历链表;
pre=L;
while(pre->next!=NULL)
if(pre->next->data <= max && pre->next->data >= min)
p = pre->next;
pre->next = p->next;//改变pre的后继结点;
delete p;
else if(pre->next->data>max)//因为是有序链表,所以如果数据大于删除区间的最大值就已经完成了删除。
break;
else //pre->next->data < min的情景。
pre=pre->next;//要继续往下遍历;
end if
end while
}
-
具体代码及实现结果:
-
有序链表的合并:实质上就是把L2中每个结点插入L1中相应的位置,插入结果使L1中的数据依然有序;
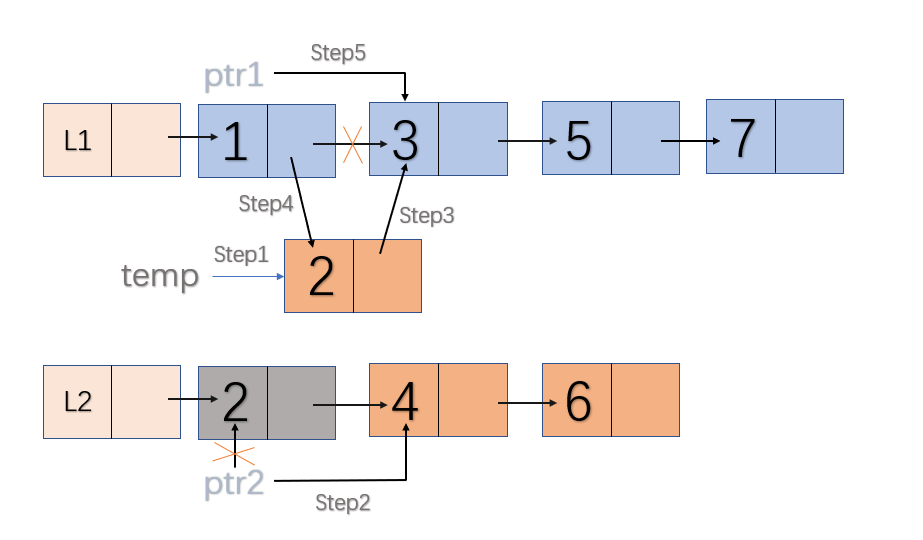
- 伪代码:
void MergeList(ListNode& L1, ListNode L2)//合并链表,使结果呈递增排序
{
定义结构体指针ptr1和ptr2分别用来遍历L1和L2;
定义结构体指针temp;
ptr1=L1;
ptr2=L2->next;
while(ptr2!=NULL)
if (ptr1->next->data > ptr2->data)//找到L1中可插入的位置
temp = ptr2;//用于保存L2中需要插入的结点;
ptr2 = ptr2->next;//继续遍历L2;
/*把temp插入L1中*/
temp->next=ptr1->next;
ptr1->next=temp;
else if (ptr1->next->data==ptr->data)//用于删除重复的数据
ptr2=ptr2->next;//跳过重复数据;
end if
ptr1=ptr1->next;
if(ptr1->next==NULL && ptr2!=NULL)//链表L1遍历完毕L2没有遍历完
ptr1->next=ptr2;//直接L2中剩余的结点连接到当前ptr1指向结点的后面
break;
end if
}
- 具体代码及实现结果:

5.双链表
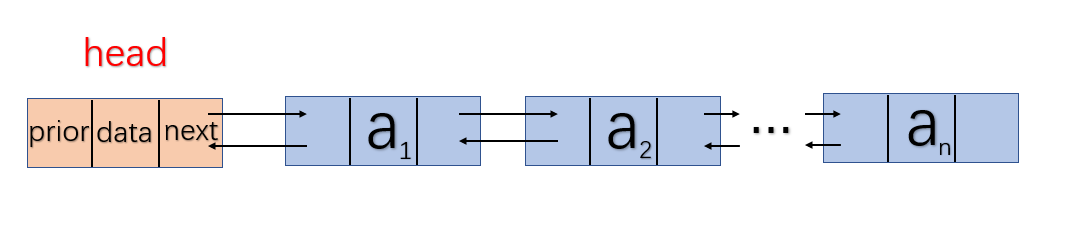
结构体定义
struct Node
{
ElemType data;
struct Node *prior;//指向前驱结点;
struct Node *next;//指向后继结点;
};
特点
- 从任意一结点出发都可以找到该结点的前驱和后继结点;
- 不论从哪个结点出发,都可以访问到其他的结点,单链表只能访问该结点后面的结点。
- 在进行插入和删除的时候不需要再定义一个前驱指针,使用双链表的前驱指针就可以对链表进行插入和删除;
6.循环链表
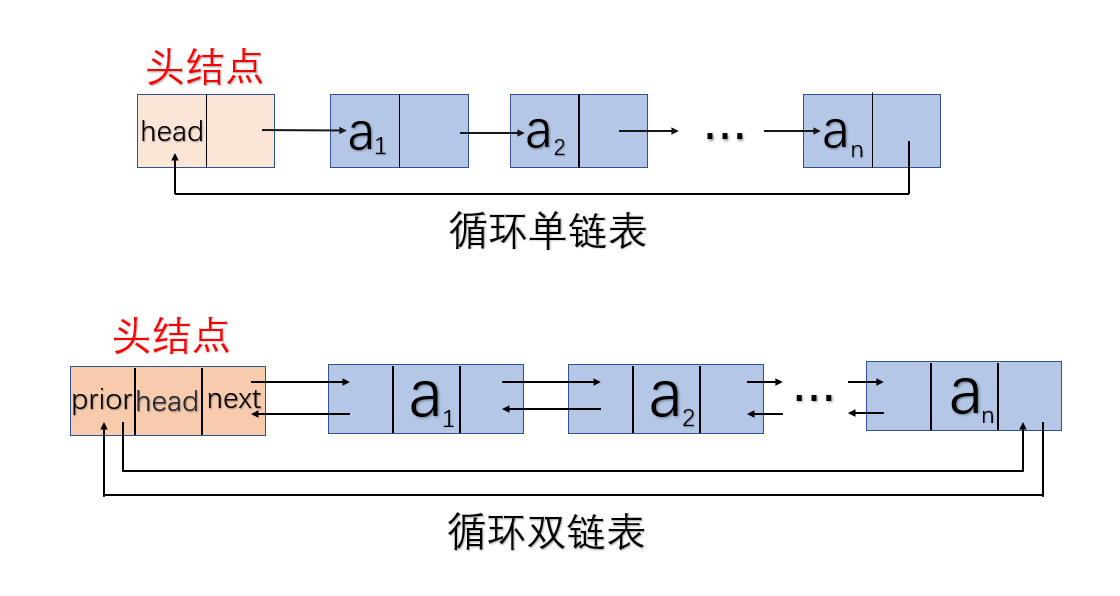
- 循环单链表:结点类型和非循环单链表相同,不同的是循环单链表将表中尾结点的指针域改成指向表头结点,整个链表形成一个环。由此中任一结点出发均可找到链表中任意一点。
- 循环双链表:结点类型和非循环双链表相同,不同的是循环双链表将表中尾结点的后继指针改成指向表头的前驱指针,表头的前驱指针指向尾结点的后继指针。
1.2对线性表的认识及学习体会
线性表的知识点很多,也很灵活。刚开始学的时候还有点生涩,不是很会用。经过这两周的学习对线性表已经有了一个大概的轮廓。但是平常做题目的时候还是会漏掉一些细节,导致程序出问题。比如在构建链表的时候,我经常会忘记让我的尾结点指向NULL,输出时陷入死循环导致程序崩溃。即使在我已经理解的情况下,还是会有许多小的细节可能会漏掉,我觉得应该是我不太够熟练,代码刷的还是不够多,接下来要多刷代码,多总结总结遇到的问题及解决方法。关于线性表的学习才刚刚开始,稍稍接触了一下一章的栈,感觉现在学的好像还只是线性表的一些皮毛(或许连皮毛都算不上),未来需要我们学习的还有很多多多多多多多的。
2.PTA实验作业
2.1 链表倒数第m个数
2.1.1代码截图
方法一:

方法二:
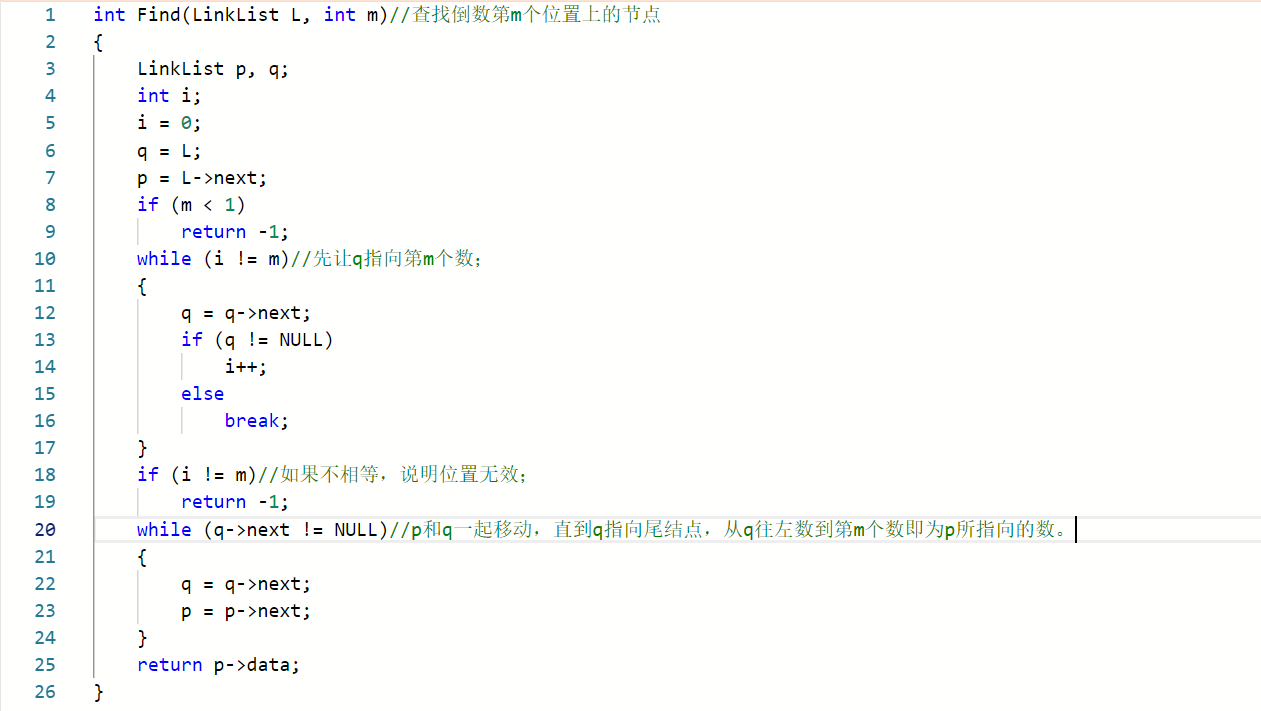
2.1.2本题PTA提交列表说明
这道题我试了上面两种方法,在试不同方法时遇到了不同错误。
方法一:
Q:运行时错误
A:起初不知道运行时错误是什么意思,以为是网页有问题于是就多试了几下。后来发现是因为我没有让链表的尾结点指向NULL,因为在自己写代码的时候没有实现销毁链表这一函数,所以我的程序能运行成功并输出正确的答案。但是在过测试的时候,由于需要执行销毁链表,找不到尾结点,程序就无法结束导致运行错误;
方法二:
Q:部分正确
A:刚开移动q时,用的是for循环,循环变量i是从1开始,当q指向第m个数退出循环时,i等于m+1,不等于m,而我下面用i==m时来判定位置合法,i!=m时位置无效,显然无论我输入的m是否合法,其结果都是无效;
Q:部分错误
A:我没有发现上面那个错误,修改了判断位置是否有效的条件,导致原本位置应该无效的变成有效的,最后对空指针进行取值导致位置无效的测试点段错误。
Q:部分错误
A:判断位置是否有效的条件少了一个等号;
Q:编译错误
A:复制代码时没有把最后的大括号复制进来;
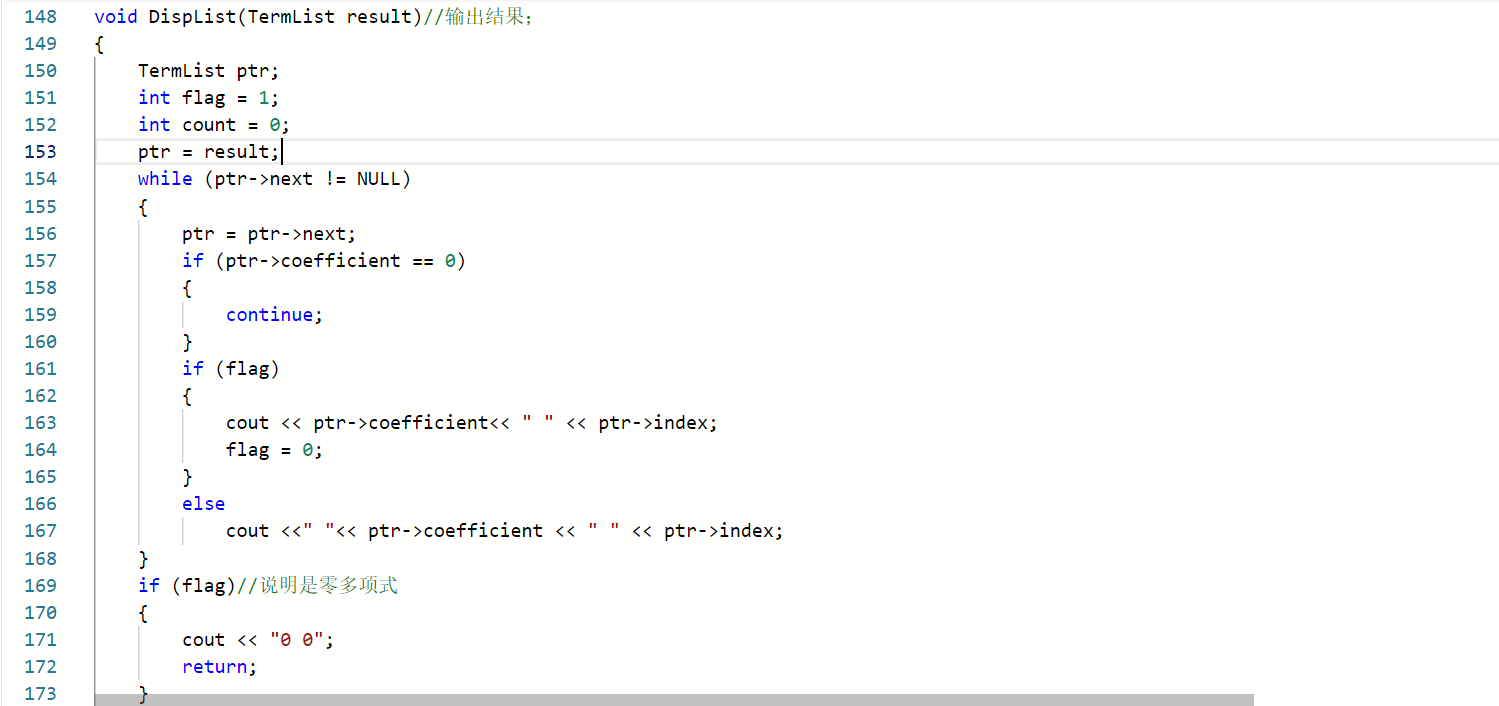
2.2一元多项式的乘法与加法运算
2.2.1代码截图




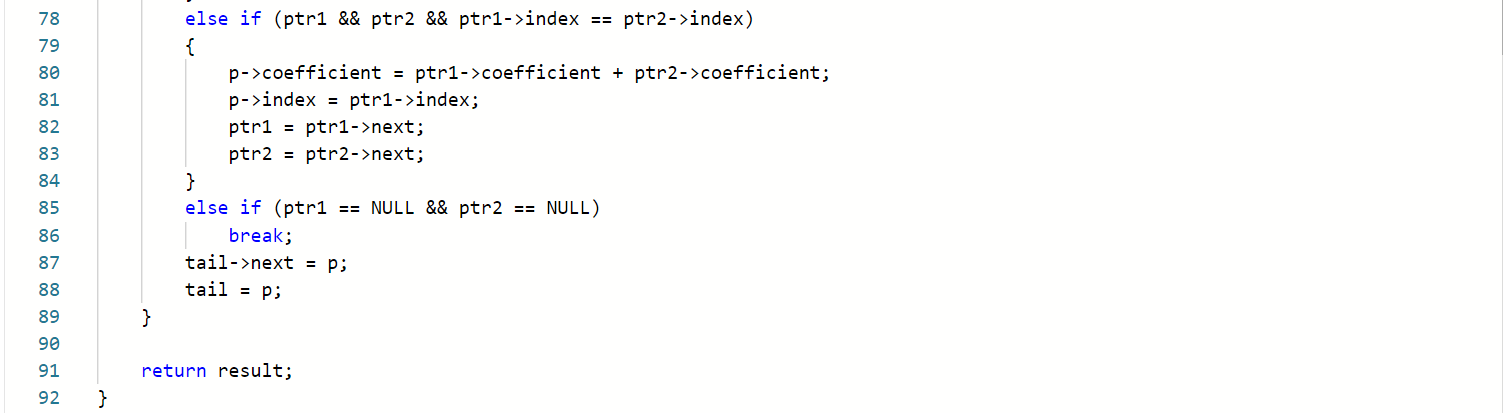
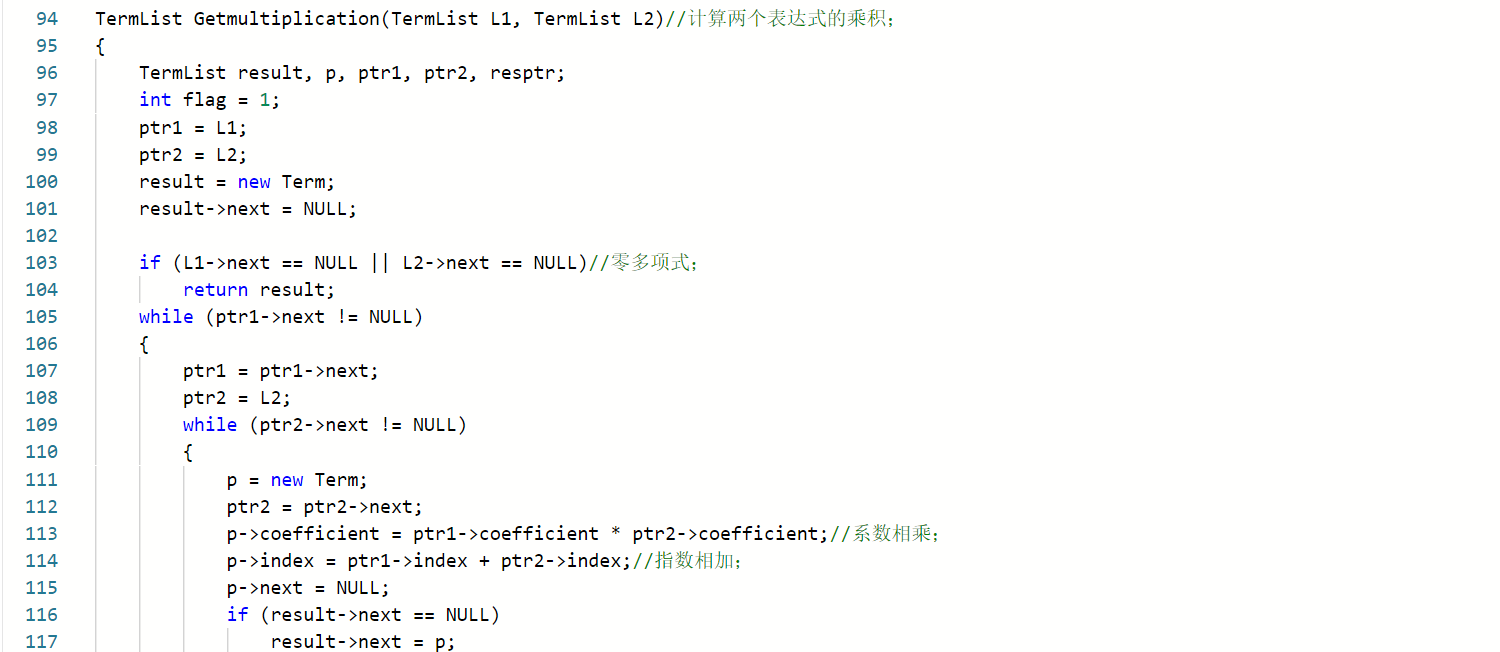
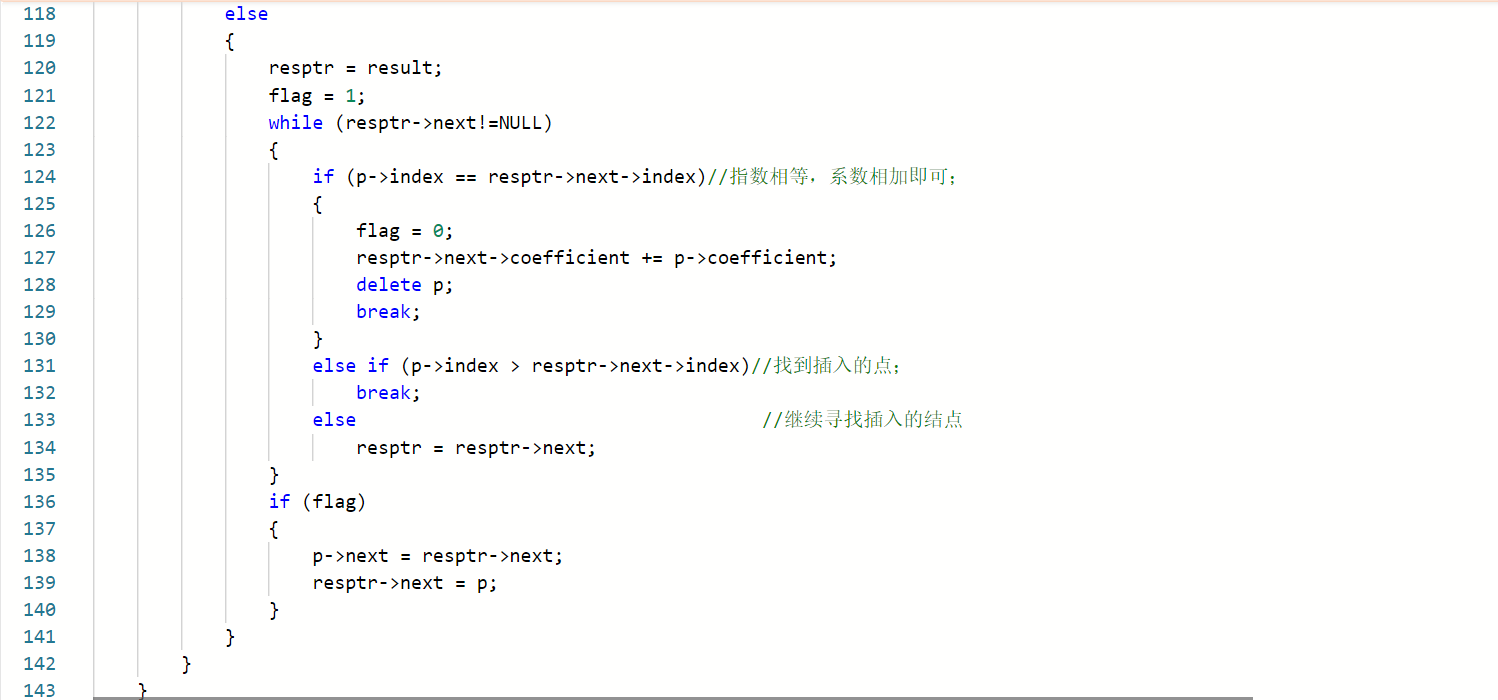


2.2.2本题PTA提交列表说明

Q:部分错误
A:没有考虑到同项需要再进行相加减;
Q:部分错误
A:同项相消时为0,输出时,要舍去不输出,我全部都输出了。
Q:部分错误
A:当结果为零多项式时,我没有输出,因为为0的全部都跳过输出了。于是我设置了变量flag,只要有输出就改变flag的值,如果flag的值没有改变,则表结果为零多项式,需要输出0 0
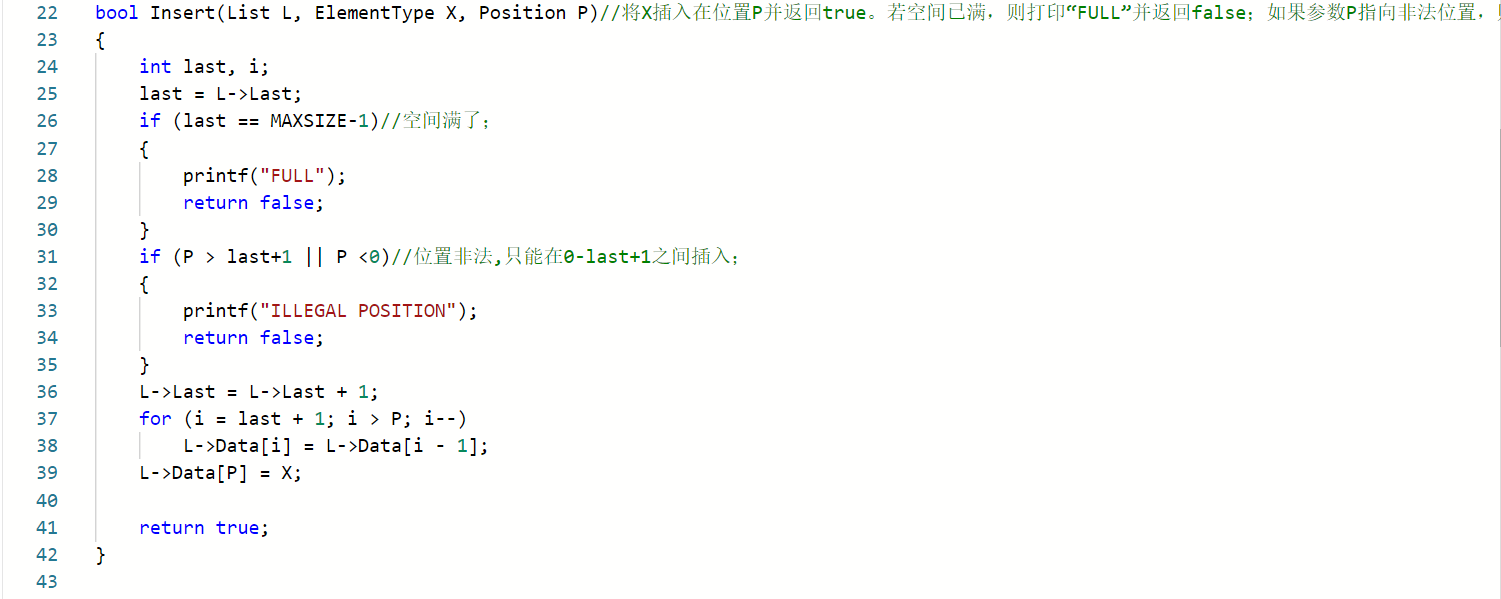
2.3顺序表的操作
2.3.1代码截图


2.3.2 本题PTA提交列表说明
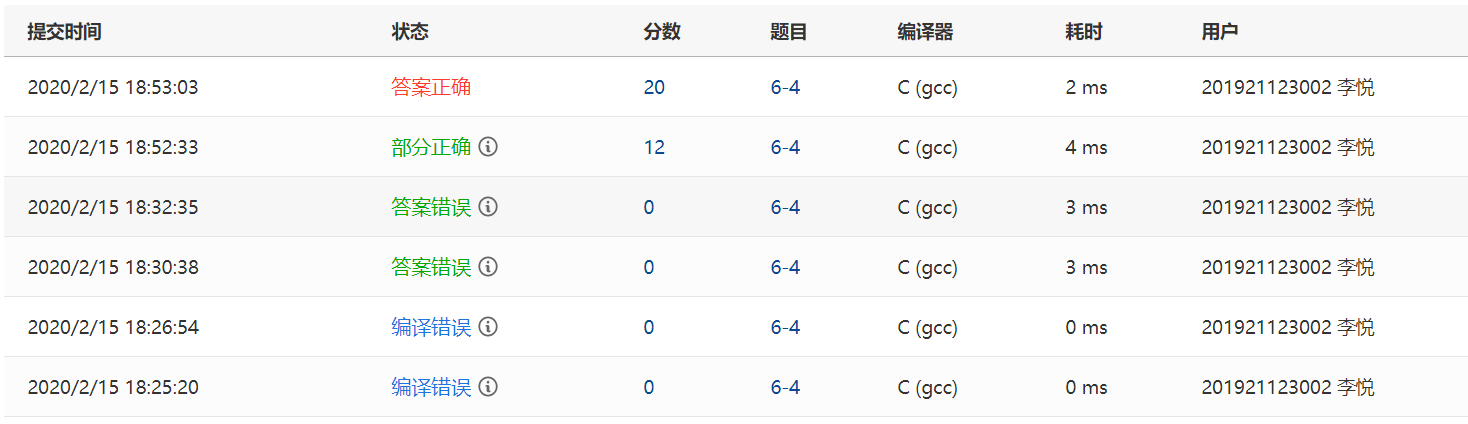
Q:编译错误
A:我编程时用的是C++的语法,而题目规定用c语言
Q:答案错误
A:题目理解错误,我以为读顺序表的插入只能插入数组的最后一位数后面。
Q:答案错误
A:删除数据的函数中,判断位置是否合法的条件错误,非法的应该是小于0或者大于last,我写的是大于MaxSize或者小于last。
Q:部分错误
A:不小心将自己为了方便在vs中调试而设置的输出代码一起复制进来。
3.阅读代码
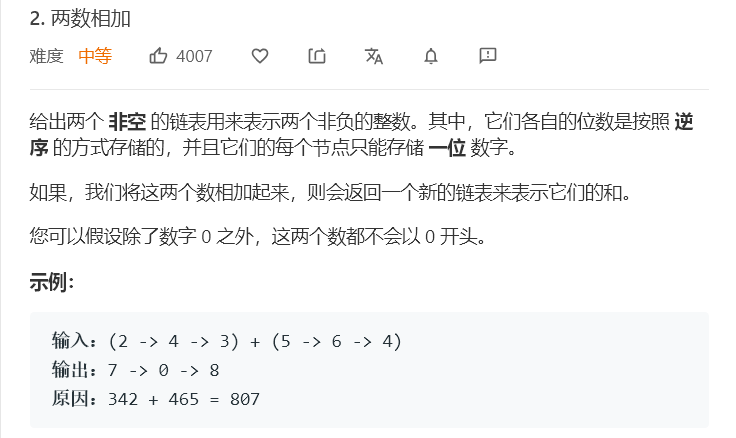
3.1 两数相加
- 题目
- 代码
class Solution {
public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
ListNode sum = l1;
while(l1.next!=null&&l2.next!=null){
l1.val += l2.val;
l1 = l1.next;
l2 = l2.next;
}
l1.val += l2.val;
if(l1.next==null&&l2.next!=null){
l1.next = l2.next;
}
l1 = sum;
while(l1.next!=null){
if(l1.val>9){
l1.val -= 10;
l1.next.val++;
}
l1 = l1.next;
}
if(l1.val>9){
l1.val -= 10;
l1.next = new ListNode(1);
}
return sum;
}
}
作者:lhpyxjn75x
链接:https://leetcode-cn.com/problems/add-two-numbers/solution/2liang-shu-xiang-jia-jian-dan-bao-li-2ms-by-lhpyxj/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
3.1.1 设计思路
直接从两个链表的第一位开始相加,其结果全部保存到l1中,然后开始考虑进位问题,这里要注意当l1链表中最后一个数与l2链表中的数相加需要进位时,l1必须要开拓新的空间来保存新的数。
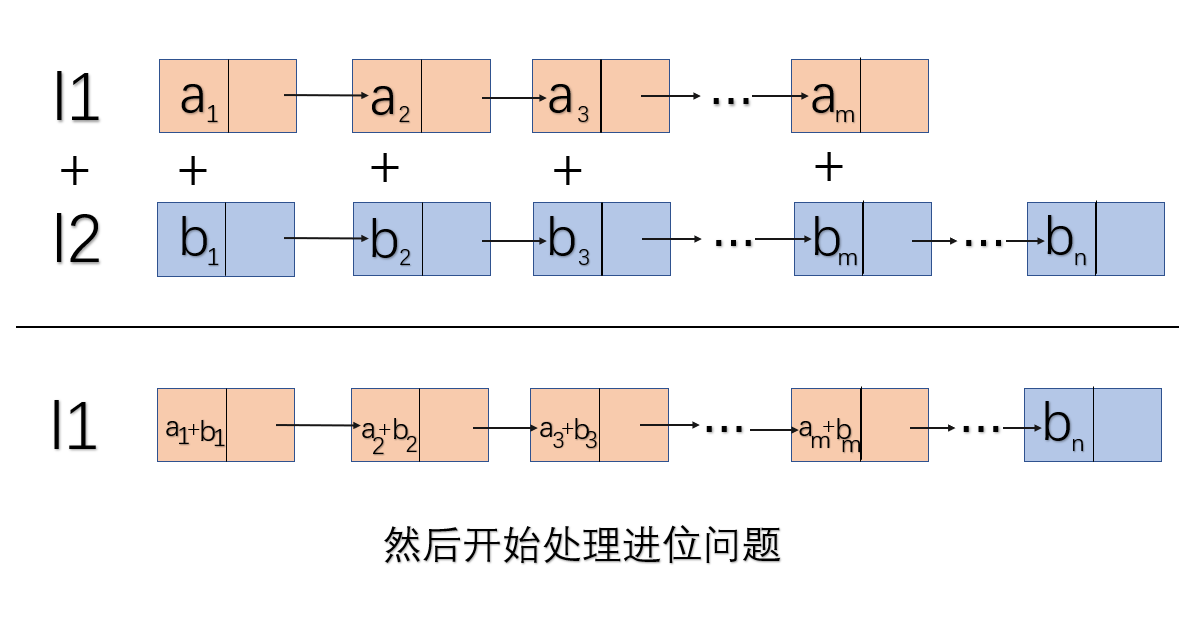
设l1保存了m位数,l2保存了n位数。
- 时间复杂度O(m+n):第一个while循环遍历了min(m,n)次,第二个while循环遍历了max(m,n)次,所以时间复杂度为O(m+n)。
- 空间复杂度O(1):因为进行相加时,把每位数相加的结果都保存到l1中,只有最后一位数相加进位需要开辟一个空间去保存,所以空间复杂度为O(1)。
3.1.2 伪代码
定义一个结构体指针sum来保存l1的头指针;
while(l1->next!=NULL && l2->next!=NULL)//把两个数每一位都先进行相加;
l1->val += l2->val;
l1 = l1->next;
l2 = l2->next;
end while
l1->val += l2.val;//循环遍历到l1和l2中有一个后继结点为NULL时停止,退出循环时当前的位上的数还未相加
if(l1->next == NULL && l2->next!=NULL)//l2的位数比l1多直接把l2后面的数连接到l1后面
l1->next=l2->next;//直接把l2后面的数连接到l1后面
end if
l1=sum;//指向头指针;
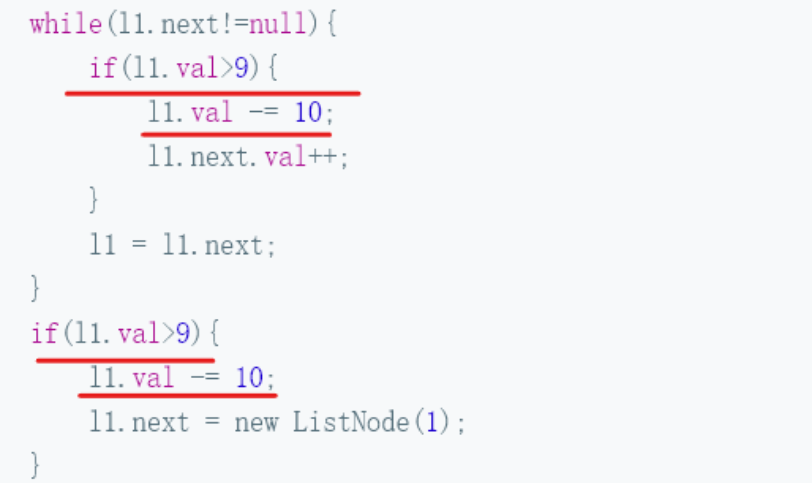
while (l1->next!=NULL)//开始处理进位问题;
if(l1->val>9)
l1->val-=10;
l1->next->val++;
end if
l1=l1->next;
end while
if(l1->val>9)//遍历到最后一位数时,如果需要进位,必须要开辟新的空间
l1->val-=10;
l1->next=new ListNode(1);
end if
return sum;
3.1.3 运行结果
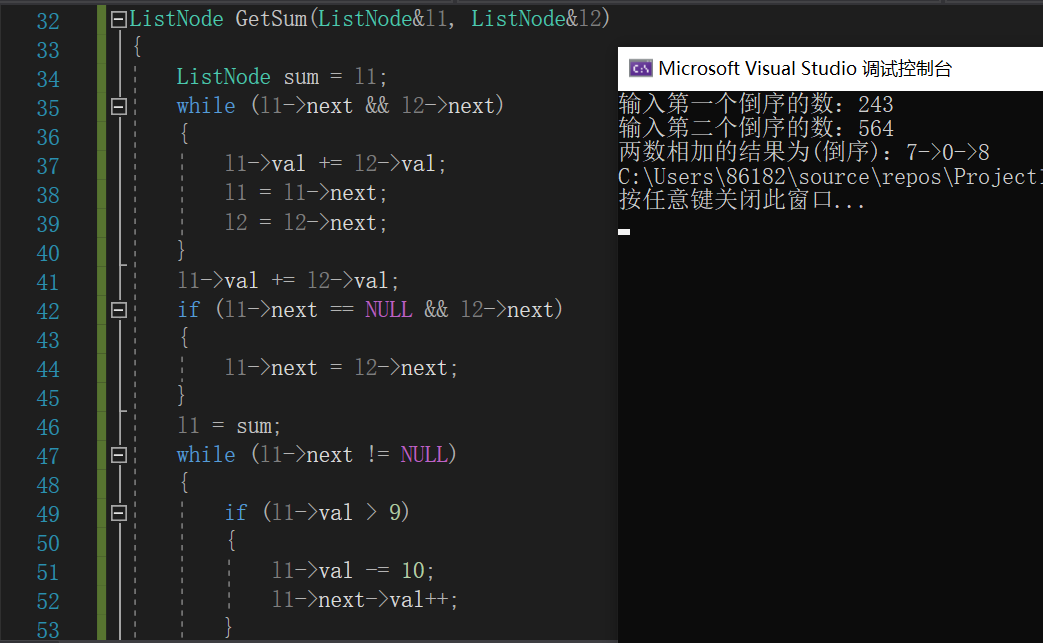
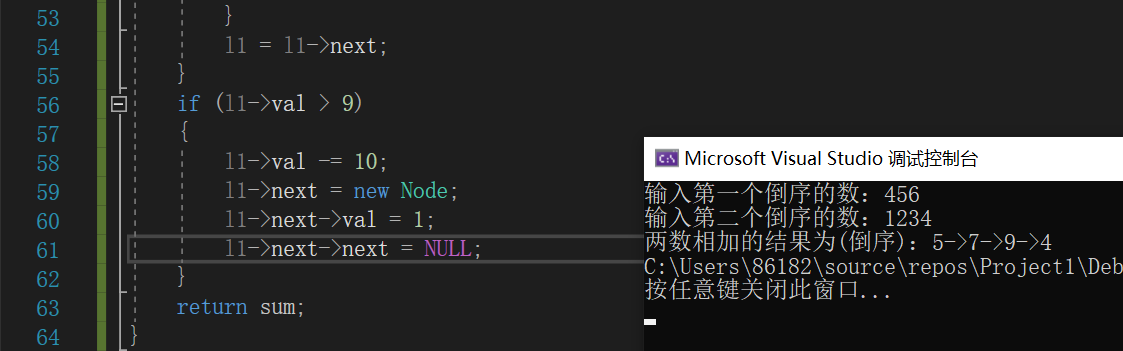
3.1.4分析该题目解题优势及难点
优势:这道题目要求我们求两数相加,按照我们的惯常思维都是从两数的最小位开始计算,题目很友好的将输入的数据变为逆序的,很大程度上减轻了我们写代码的负担,我们只需要按照小学学习的知识结合代码完成就可以了。
难点:对于我们用惯含头结点的链表来说,写代码测试的时候就需要费点心思,不可按照原来有头结点的写法来创建链表或者来判定是否跳出循环。而且从这位作者的代码可以看到,这段代码有两处地方看起来可以归并到循环里面的代码,但是却又被单独挑出来执行的,这两处地方要特别注意,如果全部都归并到循环中,就会使l1指向空指针并对空指针进行取值的错误操作。

3.2 两两交换链表中的结点
- 题目:
- 代码:
class Solution {
public ListNode swapPairs(ListNode head) {
if(head == null || head.next == null){
return head;
}
ListNode next = head.next;
head.next = swapPairs(next.next);
next.next = head;
return next;
}
}
作者:guanpengchn
链接:https://leetcode-cn.com/problems/swap-nodes-in-pairs/solution/hua-jie-suan-fa-24-liang-liang-jiao-huan-lian-biao/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
3.2.1 设计思路
从链头开始把两个两个节点看成一个整体,每个整体中的两个节点交换后,原本为第一个结点的总是连接下一个整体的第二个结点(交换后变成下一个整体的第一个结点),这样我们可以设置一个递归算法,先递进到最后两个数或者一个数后,从后面的数据开始进行交换,交换完成后返回到上一级。对当前整体中的第一个结点连接上后面已经进行交换后的数据,再把当前整体中第二个结点移动到第一个结点前面。
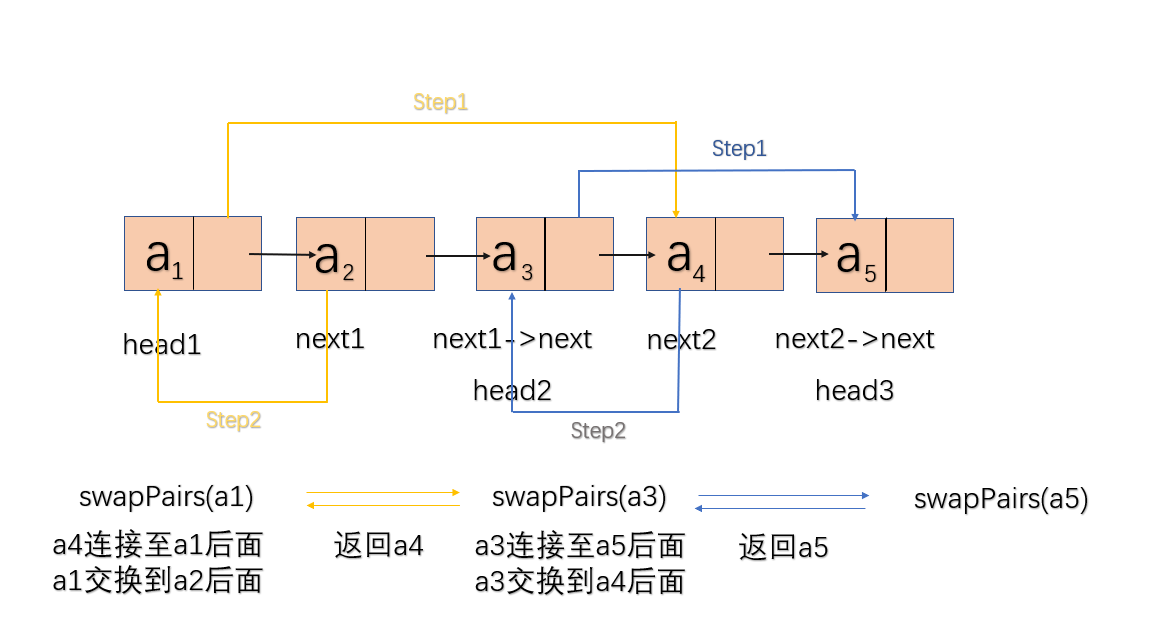
设该链表有n个结点:
- 时间复杂度O(n):递归次数为n/2,每次递归时需要操作的次数为4次,所以时间复杂度为T(N)=4*(n/2)+1=O(N);
- 空间复杂度O(n):递归次数为n/2,每次递归就占用会占用一个空间,所以空间复杂度为T(N)=n/2=O(N);
3.2.2 伪代码
if head == NULL || head->next==NULL //结束标志,不管head为NULL还是为最后一个节点,都不影响,一位递归回去的指针总是当前整体中的第一个结点;
return head;
end if
ListNode next=head->next;//next指向当前整体中的第二个结点;
head->next = swapPairs(next->next);//当前整体中的第一个结点先连接上已经交换过结点后的下一个整体中的第一个结点(就是原来该整体的第二个结点)
next->next=head;//将该整体的第一个结点移动到第二个结点后面;
return next;//原本的第二个结点现在变成这个整体中的第一个结点,返回到上一级函数。
3.2.3 运行结果

3.2.4 分析该题目解题优势及难点
优势:这道题使用非递归算法也没有问题,例如开辟一条新的链表用于保存交换后的数据,思路比较简单,时间复杂度和递归算法相同,但是空间复杂度为0(1)比递归算法要小,即使想不出递归算法,运用非递归算法也比较容易实现;
难点:我觉得这道题的难点在于使用递归算法的时候,当我看到这个代码的时候我是懵的(神奇)。递归算法的整个思维很巧妙且灵活,光是理解这段代码就耗费了我一个晚上的时间。递归算法还是要多画图,睁眼瞎看真的看不出什么来(黑眼圈警告!)。