函数式编程之-重新认识泛型(1)

如果问C#这门语言那些特性是非常好的设计，那么泛型肯定是其中一个。泛型的引入间接带来了LINQ，大家大概都享受过LINQ带来的快感。泛型这个特性来自于函数式语言，F#的设计者Don syme参与了.NET中的泛型设计。C#中的泛型特性使用起来也很简单，以至于没有任何函数式基础就能把LINQ耍起来。本文将从函数式语言的角度来分析泛型，进而描述为什么会有Select、SelectMany这样的函数。
大家一定只用过List<T>这个泛型类型，当然你自己一定也设计过某种泛型类，比如Repository<T>等。在函数式编程之-拒绝空引用异常(Option类型)一文中还提到了避免NullReferenceException的类型Optional<T>。
在函数式编程语言中，泛型的应用更加广泛，比如你在F#中定义一个方法：

let print x = printf "%A" x 

得到的方法签名如下：

val print : x:'a -> unit 

'a表示任意类型，F#中定义的方法是自动泛化的，在C#则需要手动编写泛型方法。

Select函数的来历

对于任意类型a，总有那么一个对应的泛型类型E<a>与之对应，无论是List<a>，还是Optional<a>等。我们把从a到E<a>的过程叫做提升(lifting)。在我们写代码的过程中，必然存在把a变换成E<a>，也有把E<a>变换成a的过程:

public Optional<int> Add10(Optional<int> x)
{
    if (x.HasValue)
    {
        return Optional.Some(x.Value + 10);
    }

    return Optional.None<int>();
}

上面的代码描述了一个向Optional<int>加10的过程，如果参数x中的Optional没有缺失，就把Optional<int>变为int，同时在int的基础上加10，然后再转化为Optional<int>。
用F#实现相同的逻辑：

let add10 x =
    match x with 
    | Some s -> Some (s+10)
    | None -> None

这看似很正常的代码片段，在函数式语言里是错误的思路。函数式编程语言的类型可以分为两类，类型a和被提升的类型E<a>，无论E<a>是List<a>、Optional<a>还是其他。当代码在a和被提升类型E<a>之间来回切换时，代码就会变得异常复杂:

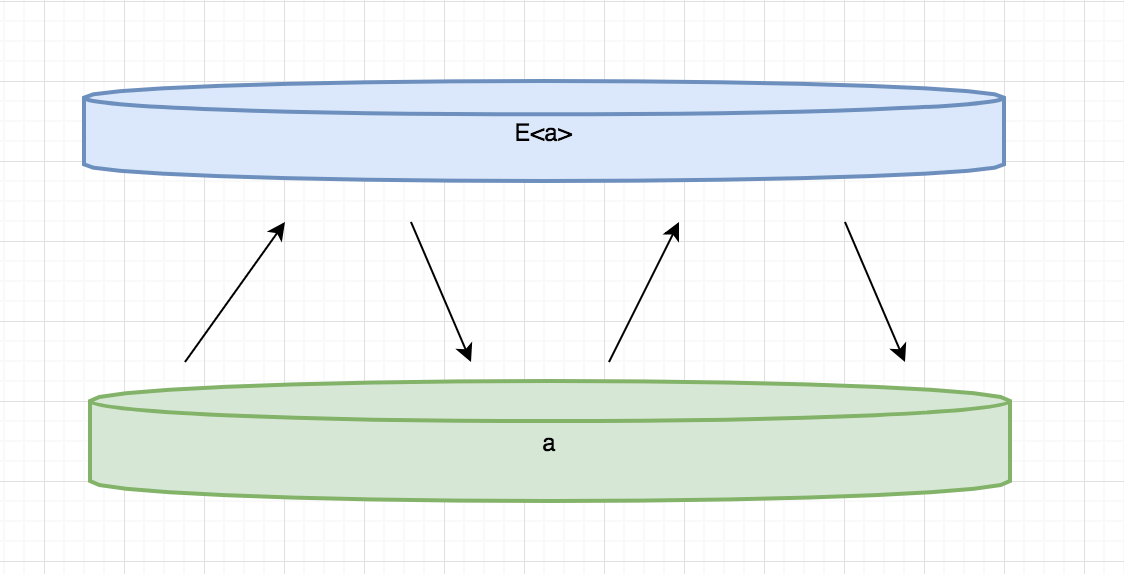
数学家就想使用一些固定的套路来解决这个问题。如下图所示，你一旦拥有某个提升类型E<a>，就应该尽可能的让他保持在提升状态。

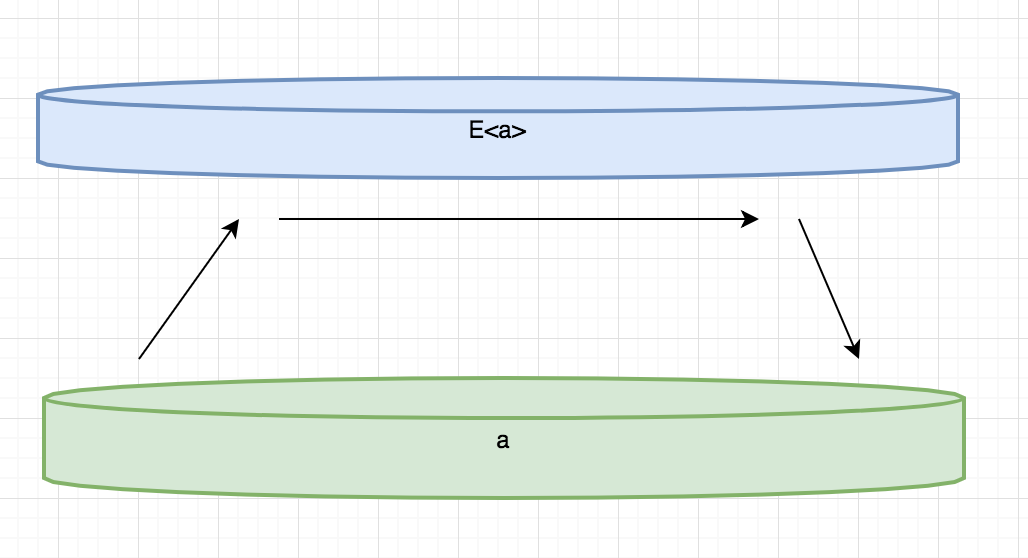
对于上面这个问题，你已经拥有一个被提升的类型Optional<int>，但是你想在Optional<int>上作用一个未被提升的函数：x = x + 10，最终想得到一个Optional<int>的结果。三个已知条件有两个是提升类型，只有函数x = x + 10是普通类型。如果存在一个函数，能够接受一个提升类型E<a>和一个普通函数a->b，并且能够返回E<b>，那么我们的问题就迎刃而解。这个函数就是Select，有的编程语言也叫做map或者lift。

F#在Option类型中已经内置了map函数:

let add10 x = 
    x |> Option.map (fun x -> x + 10)

对于C#中我们自定义的Optional<T>类型，可以添加加一个Select函数：

public Optional<T2> Select<T2>(Func<T, T2> f)
{
    if (_hasValue)
    {
        return Optional.Some(f(_value));
    }

    return Optional.None<T2>();
}

一旦Optional<T>类型有了Select方法，就可以通过下面的方式实现在Optional<int>类型上加10的需求：

public Optional<int> Add10(Optional<int> x)
{
    return x.Select(v => v + 10);
}

上面例子的函数签名如下：

Optional<T>类型中Select函数的方法签名更加泛化一些：

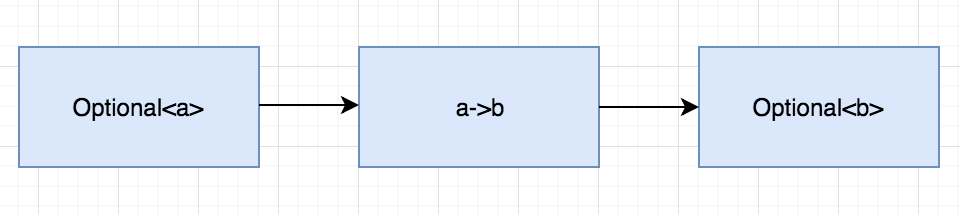
进一步泛化Select函数：

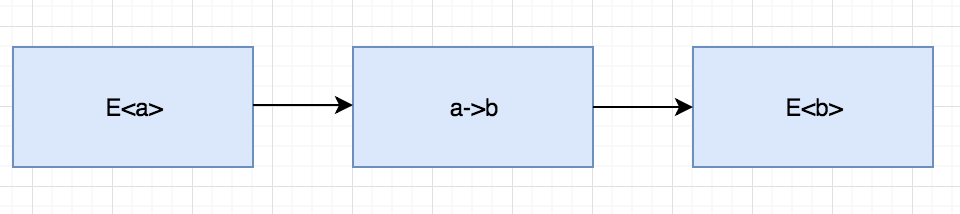
所以对Select的另类解释为：当你已经拥有一个上升的类型E<a>，如果有一个a->b的函数，在不将E<a>切换回到a的情况下得到E<b>。
上面描述的提升类型E<T>以及定义在E<T>类型下的函数Select共同组成了Functor，那么到底符合什么样的规律就被称作是Functor? 见Functor laws。

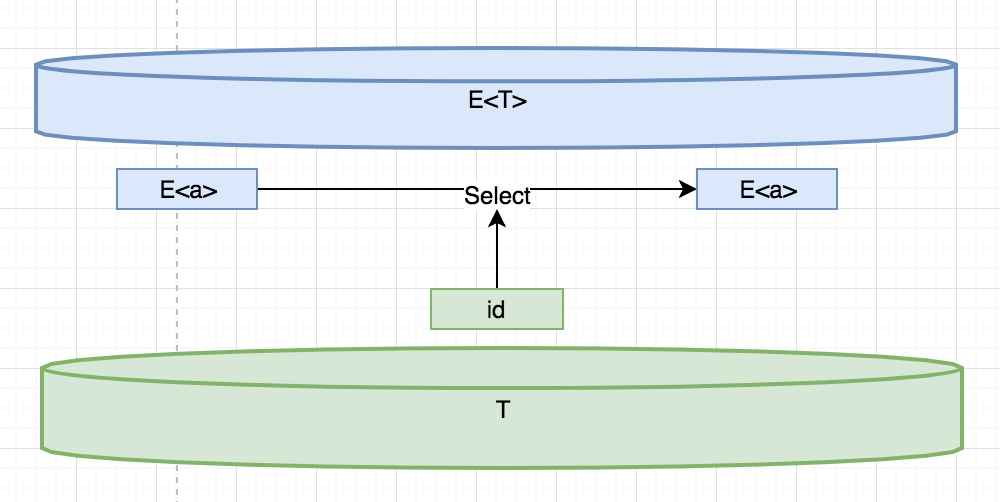
• 第一个law是说让一个被提升的类型E<a>调用Select函数，如果传入的是id函数，（所谓id函数是指输入不会被修改的函数，F#和Haskell内置了id函数）那么得到的值E<b>跟E<a>是相等的。
  

[Theory]
[InlineData("")]
[InlineData("foo")]
[InlineData("bar")]
public void OptionalObeysFirstFunctorLaw(string value)
{
    Func<string, string> id = x => x;

    var m = Optional.Some(value);
    
    Assert.Equal(m, m.Select(id));
}

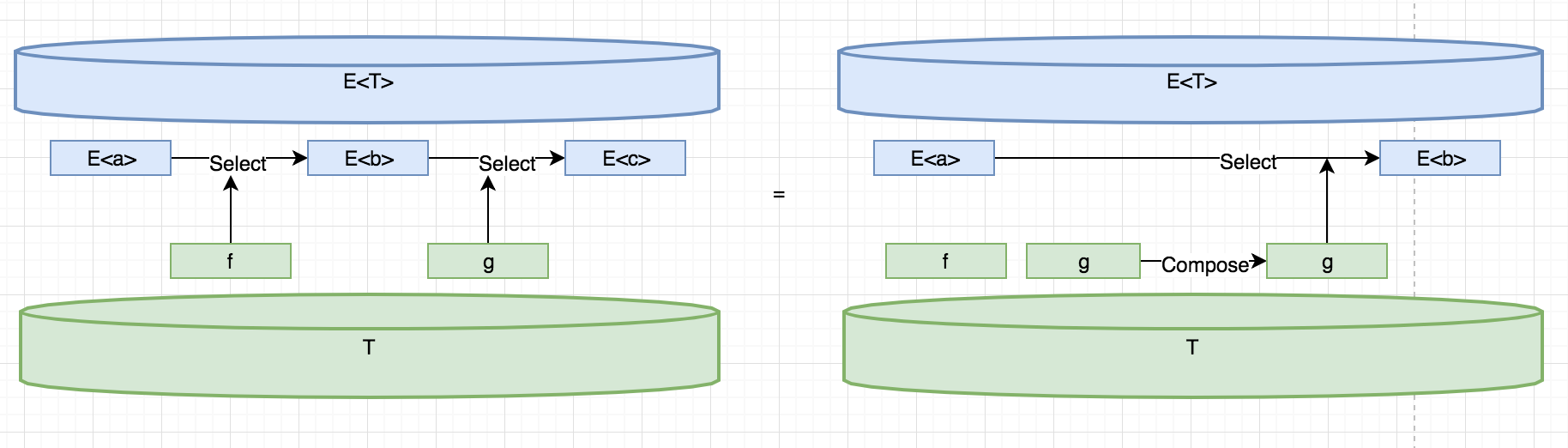
• 第二个law说存在两个函数f和g，依次Select这两个函数得到的结果，跟先把这两个函数组合起来，然后Select组合好的函数得到的结果是一致的。
  

[Theory]
[InlineData("")]
[InlineData("foo")]
[InlineData("bar")]
public void OptionalObeysSecondFunctorLaw(string value)
{
    Func<string, int> f = s => s.Length;
    Func<int, bool> g = i => i > 0;
    Func<string, bool> composed = s => g(f(s));
    
    var m = Optional.Some(value);
    
    Assert.Equal(m.Select(composed), m.Select(f).Select(g));
}