1.1 3-colorability
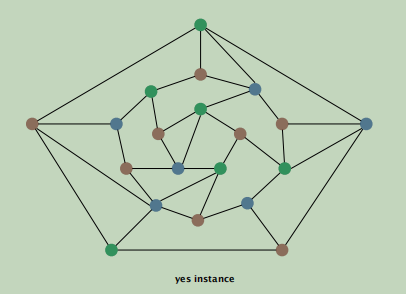
一个图的三着色问题:要使得边两头的结点颜色互不相同。
1.1.1 3元可满足规约到3着色

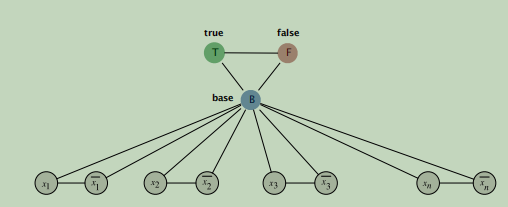
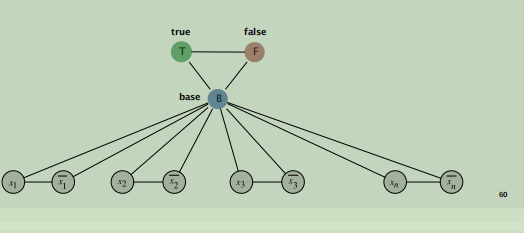
首先文法中的每一个变量和它自己的"非"连接。创建3个新结点分别为T,F,B并且将他们连接在一个三角形中。然后每一个文法都连接到B结点,对于每一个子句添加6个结点和13条边。其中B结点是基本颜色,这里假定为蓝色。
1.1.2 证明充分和必要性
定理:如果一个图是可以三着色的当且仅当这个图所对应的文法是可满足的。
Pf. ⇒ Suppose graph G is 3-colorable.
・Consider assignment that sets all T literals to true.
・(iv) ensures each literal is T or F. ・(ii) ensures a literal and its negation are opposites.
・(v) ensures at least one literal in each clause is T
如果一个图是可以三着色的,我们考虑几种分配方式使得所有的T文法都为True,确保所有的文法要么为T要么为F,至少保证有一个文法块为T。
ps:上面说的好乱,后来上油管看了下MIT的公开课才顿悟了!我们从头来理解一下:
这张图构造得很巧妙,它这样构造的目的是保证X1的值只能为true或者false而与它相连的x1'非'就只能是另外一种结果。
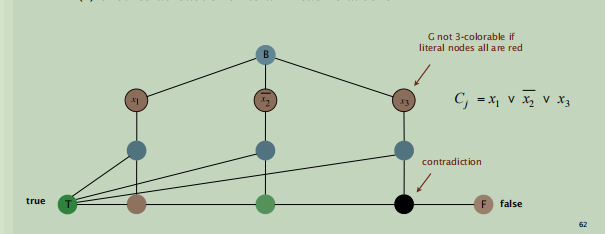
这张图也很巧妙也证明也为什么x1,x2,x3都为红(false)的时候文法式为false,它通过三着色原则强制让x1下面的结点为蓝,然后T结点右边第一个就只能为false(红色)依次推下去,发现推到F结点左边第一个结点的时候,该结点只能为红色(图中标记为黑色表示此节点跟相邻的结点有颜色冲突!)。
这个图反过来证明了为什么文法中只要一个为真就行了,可自行下来推一推。