DE(Differential Evolution)
差分进化算法是一种新兴的进化计算技术。它是由Storn等人于1995年提出的,和其它演化算法一样,DE是一种模拟生物进化的随机模型,通过反复迭代,使得那些适应环境的个体被保存了下来。但相比于进化算法,DE保留了基于种群的全局搜索策略,采用实数编码、基于差分的简单变异操作和一对一的竞争生存策略,降低了遗传操作的复杂性。
关键理念:
初为GA的变种,后自称一派
和GA,EP,ES不同,DE不是生物学启发的。
差分演化的基本框架
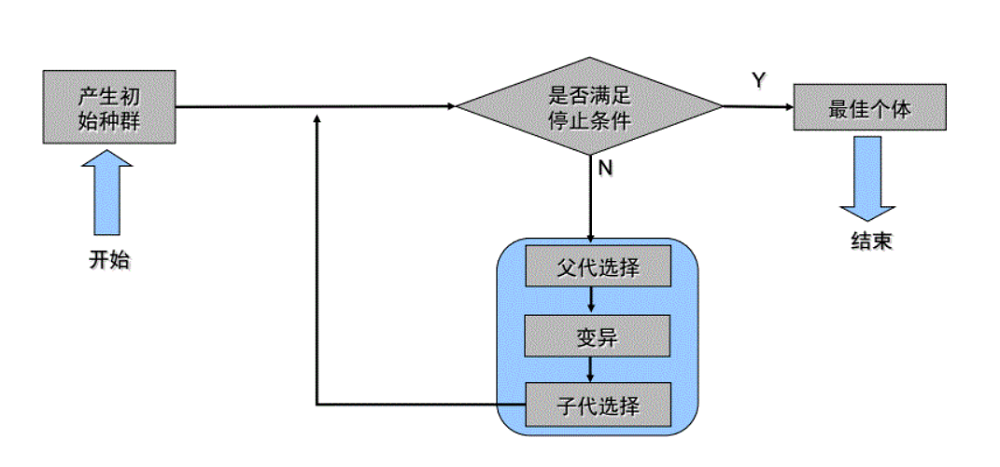
个体表示:
一般用实数编码,(x1,x2,…,xn)就是它的个体表达形式。
接下来介绍DE算法的各个部分:
父代个体选择:
基向量选择:一般有三种选择方式,1.随机从种群中选择一个个体。2.选择当前种群最好的个体。3.选择当前个体(DE的处理一般是对种群分个处理)。 产生差向量:一般可以产生1个或2个差向量,从种群中随机选取两个或多个个体相减产生。
重组:
产生实验向量:选择当前要更新的个体与变异向量交叉重组。随机产生一个概率值当它小于重组阈值时将变异向量赋给试验向量否则将当前个体赋给试验向量 产生变异向量:可以是当前基向量,或者是当前个体。需要保持试验向量至少有一维是来自变异向量的。
变异:
变异这部分有专门的公式:

当然理论上来说步长因子需要保持两性,如果设为整个种群同一个值在实验中似乎影响也不大。
存活选择:
当前子代如果好于父代,则存活。

有了这些东西我们就可以编出相应的代码:
function [answer,best]=DE(fun) global popnum ubound lbound dim F cost times best=inf; answer=zeros(times,cost/popnum); for i=1:times X=initpop(); thebest=inf; for j=1:cost/popnum for k=1:popnum [BV,DV]=PS(X); TV=variant(X(k,:),BV,DV); X(k,:)=selecsur(X(k,:),TV); end answer(i,j)=thebest; if thebest<best best=thebest; end end end function X=initpop() X=unifrnd(lbound,ubound,popnum,dim); end function [BV,DV]=PS(X) %父代选择 BV=X(unidrnd(popnum),:); %随机选取一个个体作为基向量 DV=diff(X(randperm(popnum,3),:)); %随机生成两个差向量 end function TV=variant(X,BV,DV) %变异 MV=BV+F*mean(DV); TV=zeros(1,dim); flag=0; for i1=1:dim if rand()<0.8 TV(i1)=MV(i1); flag=1; else TV(i1)=X(i1); end if flag==0 n=unidrnd(dim); TV(n)=MV(n); end end end function f=fit(X) %适应值函数 f=fun(X); end function luck=selecsur(X,newX) %生存选择 new=fit(newX); old=fit(X); if new<old good=new; luck=newX; else good=old; luck=X; end if good<thebest thebest=good; end end end
测试branin函数:
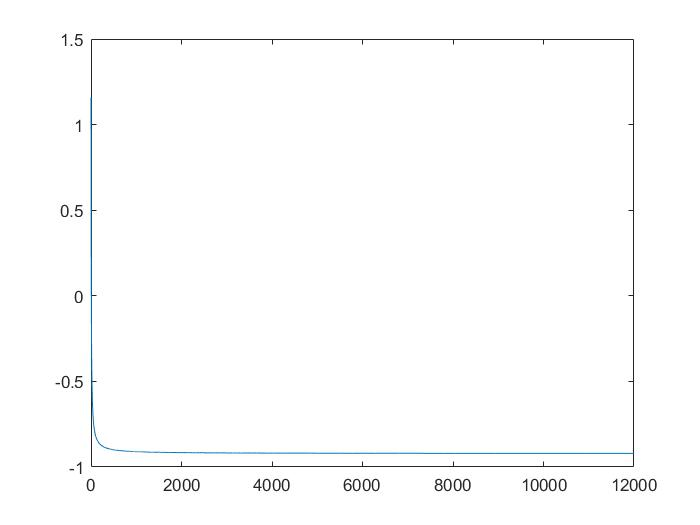
global popnum ubound lbound vs dim cost times F popnum=50; %种群数量 ubound=15; %个体维度大小上限 lbound=-5; %个体维度大小下限 F=0.7 %统一的步长 vs=0.3; %变异强度临界值 dim=2; %个体维度大小 cost=20000; %计算代价 times=30; %重复计算次数 fun=@(x)(x(2)-(5.1/(4*pi^2))*x(1)^2+5*x(1)/pi-6)^2+10*(1-1/(8*pi))*cos(x(1))+10; [answer,best]=DE(fun) %best为DE找到的最优值,answer为每次计算得到的最好结果变化矩阵 plt(answer); function plt(answer) %绘制L曲线图 hisbest=reshape(answer',1,size(answer,1)*size(answer,2)); hisbest(1)=max(hisbest); for k=2:length(hisbest) if hisbest(k)>hisbest(k-1) hisbest(k)=hisbest(k-1); end end for t=2:length(hisbest) hisbest(t)=(hisbest(t)+hisbest(t-1)*(t-1))/t; end plot(log(hisbest)); hold on end
结果如下:
转自:https://blog.csdn.net/qq_18560985/article/details/114759640?spm=1001.2014.3001.5502