线性结构Linear Structure
❖线性结构是一种有序数据项的集合,其中 每个数据项都有唯一的前驱和后继
除了第一个没有前驱,最后一个没有后继 新的数据项加入到数据集中时,只会加入到原有 某个数据项之前或之后 具有这种性质的数据集,就称为线性结构

❖线性结构总有两端,在不同的情况下,两 端的称呼也不同
有时候称为“左”“右”端、“前”“后”端、 “顶”“底”端
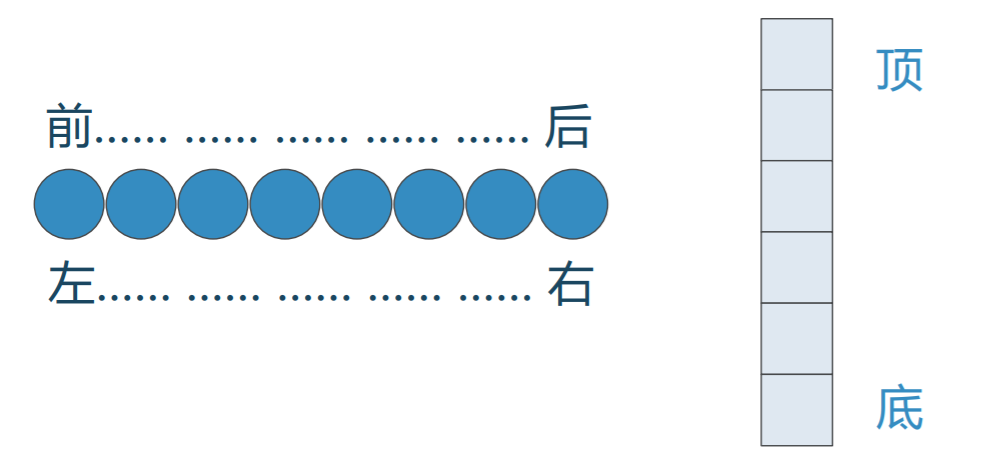
❖两端的称呼并不是关键,不同线性结构的 关键区别在于数据项增减的方式
有的结构只允许数据项从一端添加,而有的结构 则允许数据项从两端移除
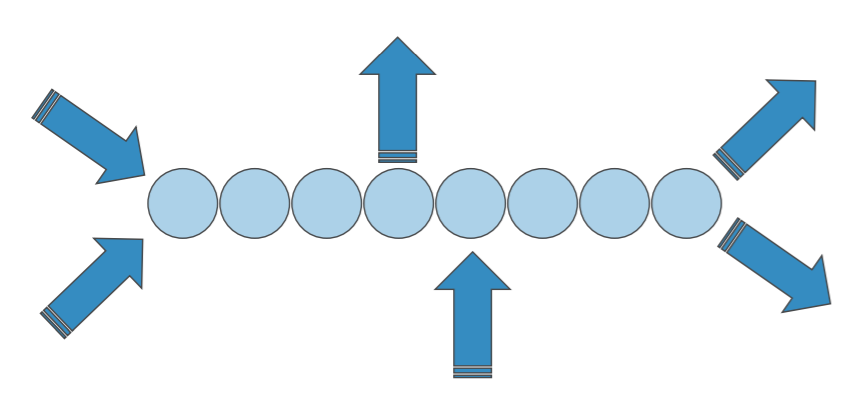
❖4个最简单但功能强大的结构:栈Stack,队列Queue,双端队列Deque 和列表List
这些数据集的共同点在于,数据项之间只存在先 后的次序关系,都是线性结构

❖这些线性结构是应用最广泛的数据结构 ,它们出现在各种算法中,用来解决大量重 要问题
 、、、
、、、
什么是栈Stack
1.栈
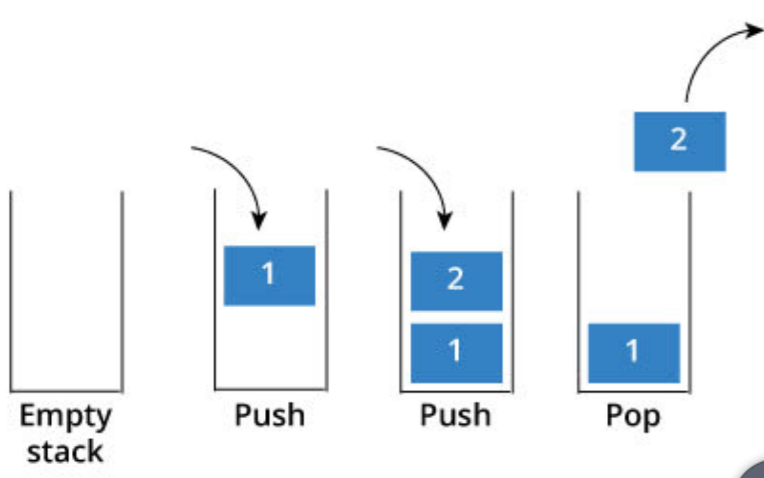
❖一种有次序的数据项集合,在栈中,数据 项的加入和移除都仅发生在同一端
这一端叫栈“顶top”,另一端叫栈“底base”
❖日常生活中有很多栈的应用
盘子、托盘、书堆等等

❖距离栈底越近的数据项,留在栈中的时间 就越长
而最新加入栈的数据项会被最先移除
❖这种次序通常称为“后进先出LIFO”: Last in First out
这是一种基于数据项保存时间的次序,时间越短 的离栈顶越近,而时间越长的离栈底越近
2.栈的特性:反转次序
❖我们观察一个由混合的python原生数据 对象形成的栈
进栈和出栈的次序正好相反
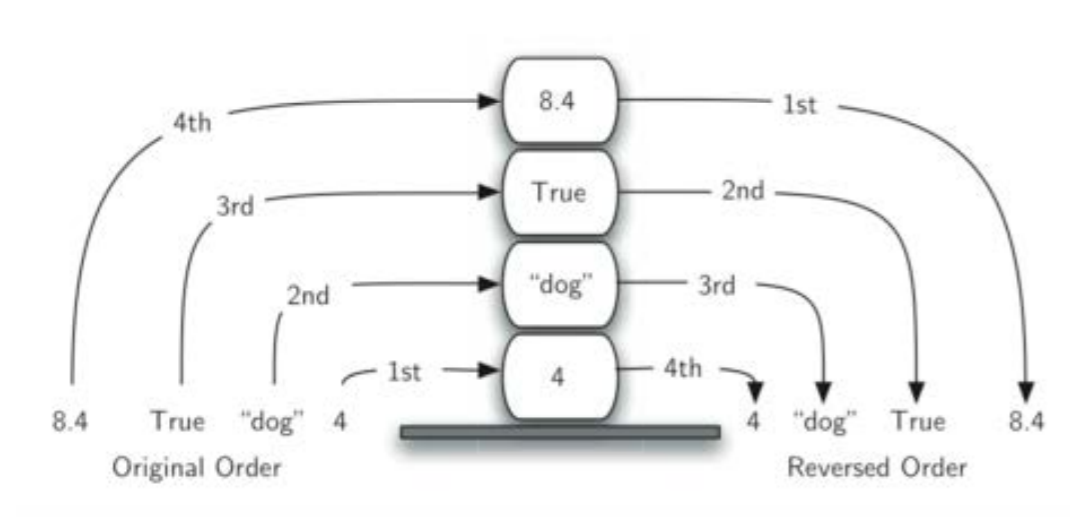
❖这种访问次序反转的特性,我们在某些计 算机操作上碰到过
浏览器的“后退back”按钮,最先back的是最 近访问的网页 Word的“Undo”按钮,最先撤销的是最近操作
3.抽象数据类型Stack
❖抽象数据类型“栈”是一个有次序的数据 集,每个数据项仅从“栈顶”一端加入到 数据集中、从数据集中移除,栈具有后进 先出LIFO的特性
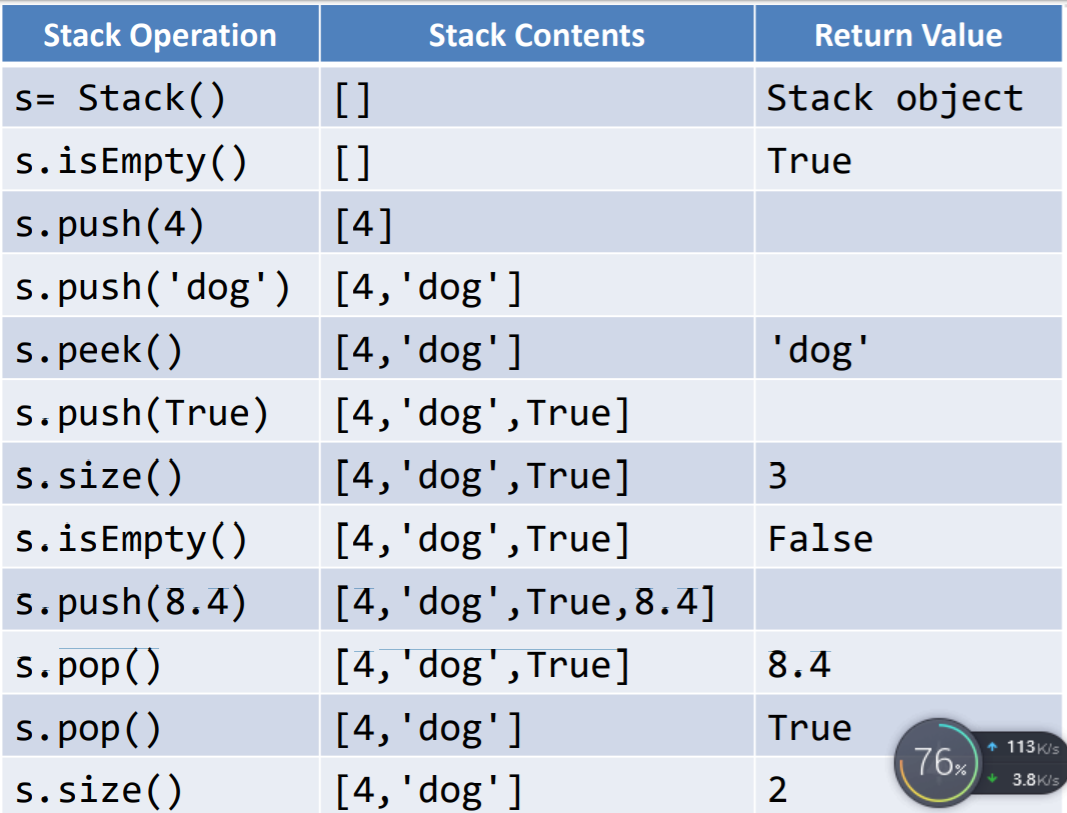
❖抽象数据类型“栈”定义为如下的操作
Stack():创建一个空栈,不包含任何数据项
push(item):将item加入栈顶,无返回值
pop():将栈顶数据项移除,并返回,栈被修改
peek():“窥视”栈顶数据项,返回栈顶的数 据项但不移除,栈不被修改
isEmpty():返回栈是否为空栈
size():返回栈中有多少个数据项

class Stack: def __init__(self): self.items=[] def isEmpty(self): return self.items==[] def push(self,item): self.items.append(item) def pop(self): return self.items.pop() def peek(self): return self.items[len(self.items)-1] def size(self): return len(self.items) s=Stack() print(s.isEmpty()) s.push(4) s.push('DOG') print(s.peek()) s.push(True) print(s.size()) print(s.isEmpty()) s.push(8.4) print(s.pop()) print(s.pop()) print(s.size())
4.用Python实现ADT Stack
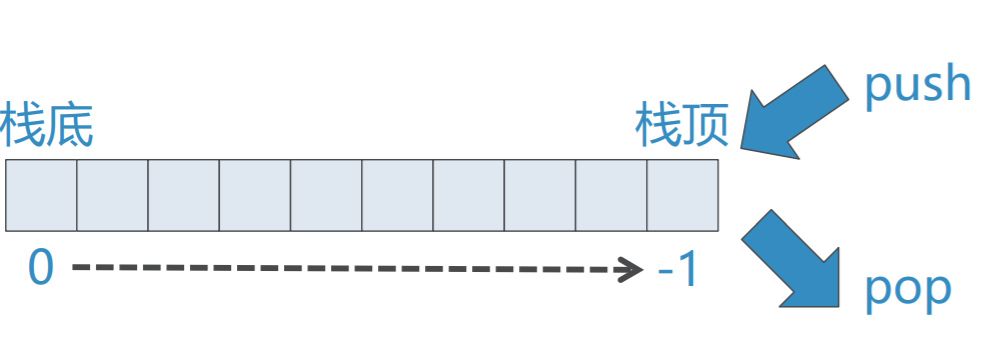
❖一个细节:Stack的两端对应list设置
可以将List的任意一端(index=0或者-1)设置 为栈顶 我们选用List的末端(index=-1)作为栈顶 这样栈的操作就可以通过对list的append和pop 来实现,很简单!
代码:
class Stack: def __init__(self): self.items=[] def isEmpty(self): return self.items==[] def push(self,item): self.items.append(item) def pop(self): return self.items.pop() def peek(self): return self.items[len(self.items)-1] def size(self): return len(self.items)
5.ADT Stack的另一个实现
❖不同的实现方案保持了ADT接口的稳定性
但性能有所不同,栈顶首端的版本(左),其 push/pop的复杂度为O(n),而栈顶尾端的实现 (右),其push/pop的复杂度为O(1)

栈的应用:简单括号匹配
1.简单括号匹配
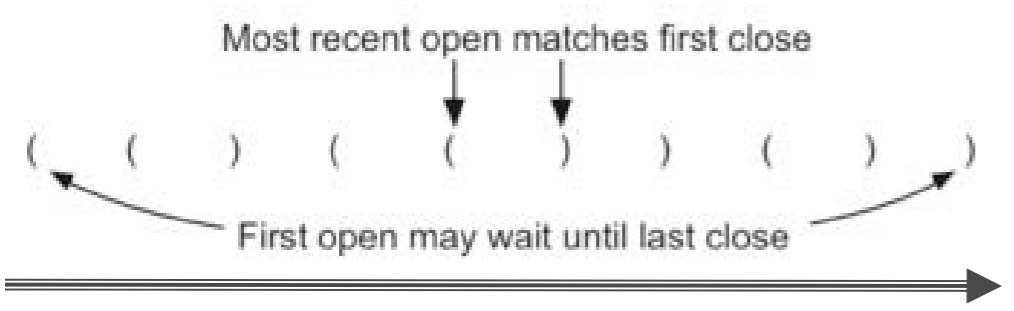
❖如何构造括号匹配识别算法
从左到右扫描括号串,最新打开的左括号,应该 匹配最先遇到的右括号 这样,第一个左括号(最早打开),就应该匹配 最后一个右括号(最后遇到) 这种次序反转的识别,正好符合栈的特性

最终代码:

class Stack: def __init__(self): self.items=[] def isEmpty(self): return self.items==[] def push(self,item): self.items.append(item) def pop(self): return self.items.pop() def peek(self): return self.items[len(self.items)-1] def size(self): return len(self.items) def parChecker(symbolString): s=Stack() balanced=True index=0 # 判断是否大于传进来参数的长循环次数度 与 balanced变量是否为真 # 如果达到这两个条件终止循环 while index<len(symbolString) and balanced: symbol=symbolString[index] #判断当前传进来的第index个字符是不是等于"C" if symbol=="(": #如果是push进栈 s.push(symbol) else: #否则判断栈是否为空 if s.isEmpty(): blanced=False else: #如果不空则将数据pop出去 s.pop() index=index+1 #balanced必须为true 数组还要为空 则true if balanced and s.isEmpty(): return True else: return False print(parChecker('(())')); print(parChecker('(()'));
2.通用括号匹配

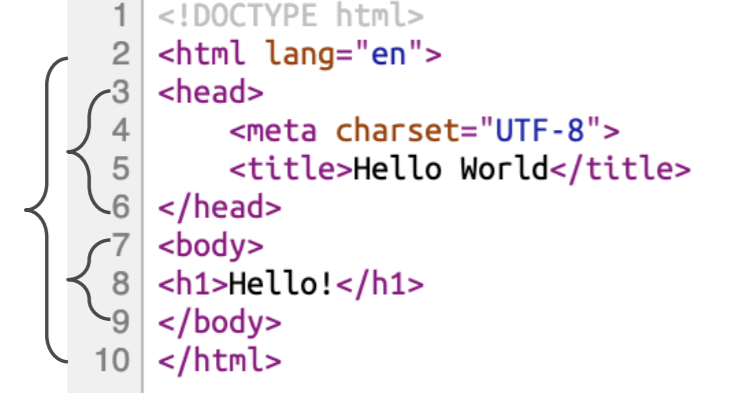
❖HTML/XML文档也有类似于括号的开闭 标记,这种层次结构化文档的校验、操作 也可以通过栈来实现
栈的应用:十进制转换为二进制
1.二进制转十进制
❖ 二进制是计算机原理中最基本的概念,作为组成 计算机最基本部件的逻辑门电路,其输入和输出 均仅为两种状态:0和1
❖ 但十进制是人类传统文化中最基本的数值概念, 如果没有进制之间的转换,人们跟计算机的交互 会相当的困难
❖所谓的“进制” ,就是用多少个字符来表 示整数
十进制是0~9这十个数字字符,二进制是0、1两 个字符
❖十进制转换为二进制,采用的是“除以2 求余数”的算法 将整数不断除以2,每次得到的余数就是由低到 高的二进制位

❖“除以2”的过程,得到的余数是从低到 高的次序,而输出则是从高到低,所以需 要一个栈来反转次序

十进制转二进制代码:

class Stack: def __init__(self): self.items=[] def isEmpty(self): return self.items==[] def push(self,item): self.items.append(item) def pop(self): return self.items.pop() def peek(self): return self.items[len(self.items)-1] def size(self): return len(self.items) def divideBy2(decNumber): remstack=Stack() while decNumber>0: rem=decNumber%2 remstack.push(rem) decNumber=decNumber // 2 binString="" while not remstack.isEmpty(): binString=binString+str(remstack.pop()) return binString; print(divideBy2(42));
2.扩展到更多进制转换
❖十进制转换为二进制的算法,很容易可以 扩展为转换到任意N进制
只需要将“除以2求余数”算法改为“除以N求余 数”算法就可以
❖计算机中另外两种常用的进制是八进制和 十六进制

❖主要的问题是如何表示八进制及十六进制
二进制有两个不同数字0、1
十进制有十个不同数字0、1、2、3、4、5、6、 7、8、9
八进制可用八个不同数字0、1、2、3、4、5、6 、7
十六进制的十六个不同数字则是0、1、2、3、4 、5、6、7、8、9、A、B、C、D、E、F
扩展到多进制代码:

class Stack: def __init__(self): self.items=[] def isEmpty(self): return self.items==[] def push(self,item): self.items.append(item) def pop(self): return self.items.pop() def peek(self): return self.items[len(self.items)-1] def size(self): return len(self.items) def divideBy2(decNumber,base): digits="0123456789ABCDEF" remstack=Stack() while decNumber>0: rem=decNumber%base remstack.push(rem) decNumber=decNumber // base binString="" while not remstack.isEmpty(): binString=binString+digits[remstack.pop()] return binString; print(divideBy2(25,2)); print(divideBy2(25,16));
什么是算法分析
11
什么是算法分析
111
