[CF1284E]New Year and Castle Construction

题面

http://codeforces.com/problemset/problem/1284/E

题解

经过持久的思考（看题解），发现直接正向去求一个点在多少个四边形内部是行不通的，所以取补，统计一个点在多少个四边形外部。

对于组成四边形的四个点和一个点P，把四个点按照与P连线的极角升序排序。设排好序后顺序是A,B,C,D，那么不管这四个点以何种顺序连接成四边形，P都在该四边形外部，当且仅当(angle APB)，(angle BPC)，(angle CPD)，(angle DPA)中有一个大于(pi)（注意：此处的(angle APB)指的是逆时针方向上以PA为始边，PB为终边的([0,2pi))之间的角，可以大于(pi)）

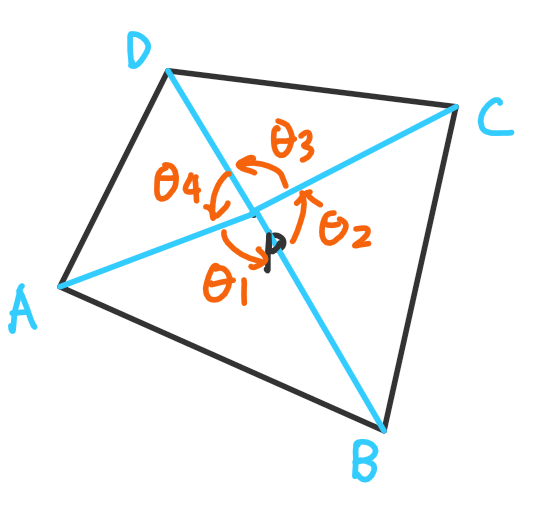
• 如图，P在四边形内部，四个角都(<pi)。

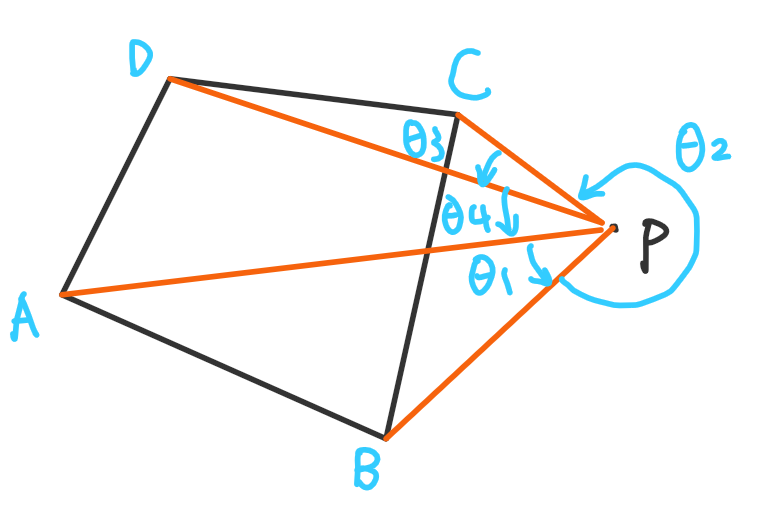
• 如图，P在四边形外部，( heta_2>pi)。

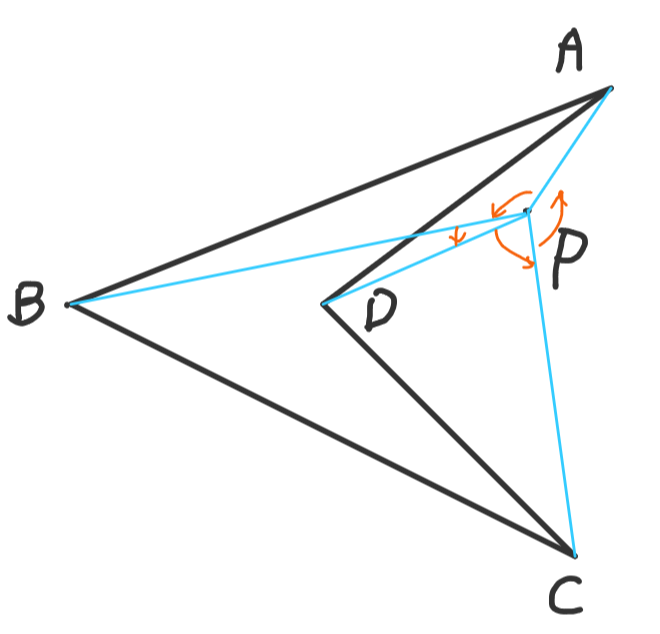
• 本图似乎是反例，其实并不是，因为这四点如果按照A-C-D-B的顺序连接，P就在四边形内部了。

所以程序的流程就很清晰了：先枚举P，然后把除了P以外的所有点极角排序，枚举这个大于(pi)的角的始边，假设终边有x个选择（终边可选择的区域的边界递增，x可均摊O(1)维护），那么此时的四边形数就是({sum_{i=0}^{k}}{ binom{i}{2}})，利用平方和公式求和即可。

总时间复杂度(O(n^2 log n))。

代码

#include<bits/stdc++.h>

using namespace std;

#define ll long long
#define rg register
#define In inline

const ll N = 2500;

In ll read(){
	ll s = 0,ww = 1;
	char ch = getchar();
	while(ch < '0' || ch > '9'){if(ch == '-')ww = -1;ch = getchar();}
	while('0' <= ch && ch <= '9'){s = 10 * s + ch - '0';ch = getchar();}
	return s * ww;
}

struct vec{
	ll x,y;
	vec(){}
	vec(ll _x,ll _y){x = _x,y = _y;}
	In friend vec operator + (vec a,vec b){
		return vec(a.x + b.x,a.y + b.y);
	}
	In friend vec operator - (vec a,vec b){
		return vec(a.x - b.x,a.y - b.y);
	}
	In friend ll Dot(vec a,vec b){
		return a.x * b.x + a.y * b.y;
	}
	In friend ll Cross(vec a,vec b){
		return a.x * b.y - a.y * b.x;
	}
	In friend bool InUpper(vec a){
		return a.y > 0 || (a.y==0&&a.x>0);
	}
}p[N+5];

struct ang{ //任意角
	vec v;ll r; 
	ang(){}
	ang(vec _v,ll _r){v = _v,r = _r;}
	In friend ang Rot180(ang a){
		if(InUpper(a.v))a.r++;
		a.v.x = -a.v.x;
		a.v.y = -a.v.y;
		return a;
	}
	In friend bool operator < (ang a,ang b){
		if(a.r != b.r)return a.r < b.r;
		bool k1 = InUpper(a.v),k2 = InUpper(b.v);
		if(k1 != k2)return k1 < k2;
		return Cross(a.v,b.v) > 0;
	}
};

ll n;
ang a[2*N+5];

In ll C2(ll x){return x * (x - 1) / 2;}

In ll C4(ll x){return x * (x - 1) * (x - 2) * (x - 3) / 24;}

In ll sum1(ll x){return x * (x + 1) / 2;}

In ll sum2(ll x){return x * (x + 1) * ((x<<1)|1) / 6;}

In ll sum(ll x){
	return (sum2(x) - sum1(x)) >> 1;
}

ll calc(ll id){
	ll cnt = 0;
	for(rg int i = 1;i <= n;i++)if(i != id)a[++cnt] = ang(p[i] - p[id],0);
	sort(a + 1,a + cnt + 1);
	ll m = cnt;
	for(rg int i = 1;i <= m;i++)a[++cnt] = ang(a[i].v,1);
	a[++cnt] = ang(vec(-1,0),2); //防溢出
	int l = 0,r = 0;
	ll ans = 0;
	for(rg int i = 1;i <= m;i++){
		ang al = Rot180(a[i]);
		while(a[l] < al)l++;
		r = i + m - 1;
		ans += sum(r - l);
	}
	return ans;
}

int main(){
	n = read();
	for(rg int i = 1;i <= n;i++){
		ll x = read(),y = read();
		p[i] = vec(x,y);
	}
	ll all = n * C4(n - 1);
	ll ans = 0;
	for(rg int i = 1;i <= n;i++)ans += calc(i);
	ans = all - ans;
	cout << ans << endl;
	return 0;
}