声明:本篇博文的内容摘自于《密码编码学与网络安全》这本书。
群、环和域都是数学理论中的一个分支,即抽象代数或称为近世代数的基本元素。在抽象代数中,我们关心的是其元素能进行代数运算的集合,也就是说,我们可以通过很多种方法,使集合上的两个元素组合得到集合中的第三个元素。这些运算方法都遵守特殊的规则,而这些规则又能确定集合的性质。根据约定,集合上元素的两种主要运算符号与普通数字的加法和乘法所使用的符号是相同的。然而,我们必须指出,在抽象代数中,我们并不仅仅限于普通的算术操作。
群(group)是一个数学概念,群论(group theory)是一门数学学科。
群G,有时记为{G, . },是定义了一个二元运算的非空集合,这个二元运算可表示为 . ,G中的每一个序偶(a,b)通过运算生成G中的元素(a.b),并满足以下公理:
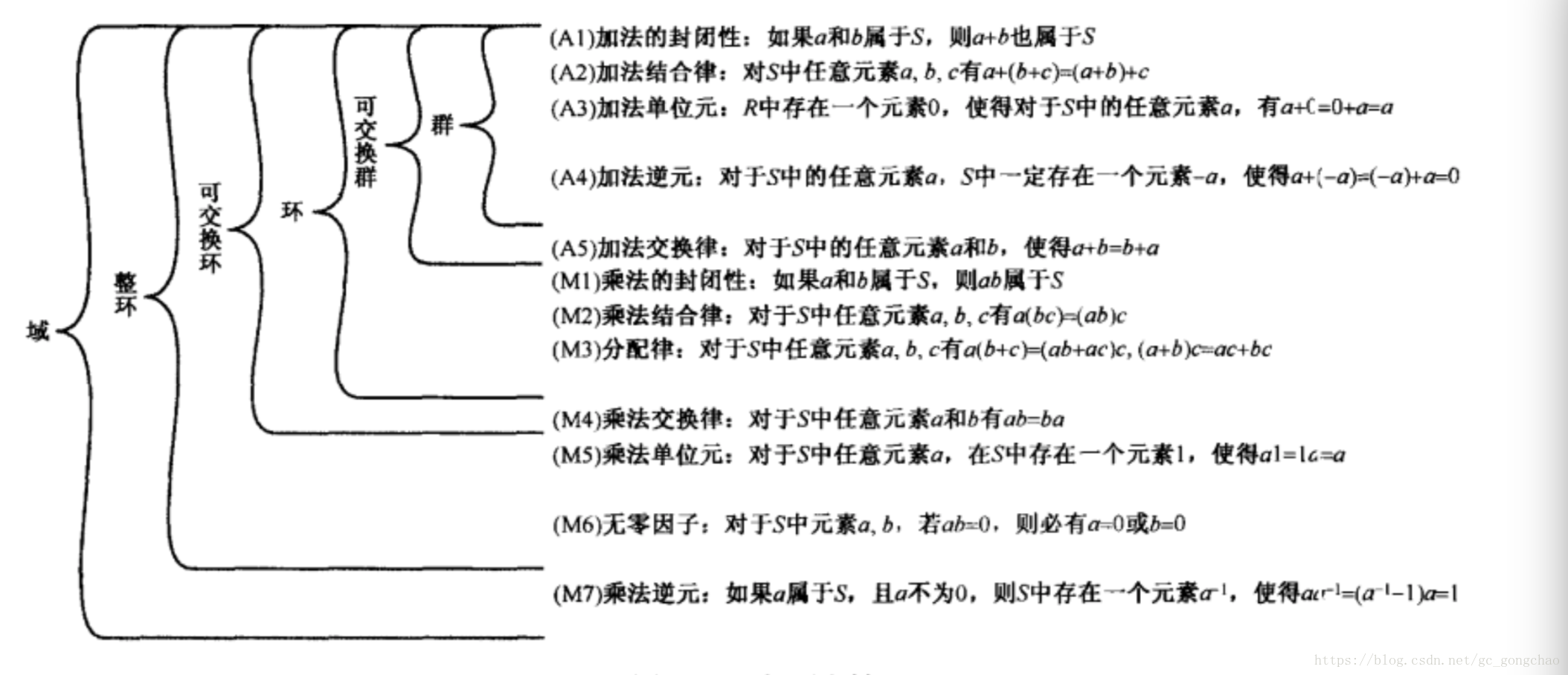
(A1)封闭性:如果a和b都属于G,则a.b也属于G。
(A2)结合律:对于G中任意a,b,c,都有(a.b).c=a.(b.c)成立。
(A3)单位元:G中存在一个元素e,对于G中任意元素a,都有a.e=e.a=a。
(A4)逆元: G中都存在一个元素a’,使得下式成立:a.a’=a’.a=e
如果一个群的元素是有限的,则该群称为有限群,并且群的阶就等于群中元素的个数。否则,称该群为无限群。
一个群如果还满足以下条件,则称为交换群:
(A5)交换律:对于G中任意的元素a,b,都有a.b=b.a成立。
循环群

环
环R,有时记为{R,+,x},是一个有两个二元运算的集合,这两个二元运算分别称为加法和乘法,且对于R中的任意元素a,b,c满足以下公理。
(A1~A5)R关于加法是一个交换群;也就是说,R满足从A1到A5的所有原则。对于此种情况下的加法群,我们用0表示其单位元,-a表示a的逆元。
(M1)乘法的封闭性:如果a和b都属于R,则ab也属于R。
(M2)乘法的结合律:对于R中的任意元素a,b,c,有a(bc)=(ab)c成立。
(M3)分配律:对于R中的任意元素a,b,c,下面两个式子总成立:
a(b+c)=ab+ac (a+b)c=ac+bc
本质上说,环就是一个集合,我们可以在其上进行加法、减法[a-b=a+(-b)]和乘法而不脱离该集合。
环如果还满足以下条件,则称为交换环。
(M4)乘法的交换律:对于R中任意元素a,b,有ab=ba成立。
下面,我们定义整环,它是满足以下公理的交换环:
(M5)乘法单位元:在R中存在元素1,使得对于R中的任意元素a,有a1=1a=a成立。
(M6)无零因子:如果有R中元素a,b,且ab=0,则必有a=0或b=0。
这里简单总结一下,群是定义了一个二元运算的集合而环是定义了两个二元运算的集合。循环群是由一个元素生成的集合。
域

有限域GF( p )

阶为p的有限域
模算术是一种整数算术,它将所有整数约减为一个固定的集合[0,1,… ,n-1],其中n为某个整数。任何这个集合外的整数通过除以n取余数的方式约减到这个范围内。
在此之前先复习一下模运算:
模数
如果a是整数,n是正整数,则我们定义 a模n 是 a除以n所得的余数。整数n称为模数。因此,对于任意整数a,我们总可以写出
a=qn+r (0<=r)
同余的性质
模运算有如下性质:
(1)如果n|(a-b),那么a与b模n同余。即如果两个整数a和b满足a-b能够被n整除,即(a-b)/n得到一个整数,那么就称整数a与b对模n同余,记作a≡b(mod n)。
(2)a与b模n同余隐含b与a模n同余。
(3)a与b模n同余并且b与c模n同余,那么隐含a与c模n同余。
运算(mod n)将所有的整数映射到集合{0,1,…,(n-1)}
模运算的性质
定义比n小的非负整数集合为Zn:
Zn={0,1,…,(n-1)}这个集合被称为剩余类集,或模n的剩余类。更准确地说,Zn中每一个整数都代表一个剩余类,我们可以将模n的剩余类表示为[0],[1],[2],…,[n-1],其中
[r]={a:a是一个整数,a同余r(mod n)}
比如模4的剩余类为:
[0]={…,-16,-12,-8,-4,0,4,8,12,16,….}
[1]={…,-15,-11,-7,-3,1,5,9,13,17,…}
...
在剩余类的所有整数中,我们通常用最小非负整数来代表这个剩余类。寻找与k是模n同余的最小非负整数的过程,称为模n的k约化。
Zn(是有乘法单位元的交换环)中整数运算的性质:
交换律:(w+x)mod n =(x+w) mod n (w * x) mod n =(x * w) mod n
结合律:[(w+x)+y] mod n=[w+(x+y)] mod n [(w*x)y] mod n=[w(x*y)] mod n
分配律:[w*(x+y)] mod n=[(w*x)+(w*y)] mod n
单位元:(0+w) mod n =w mod n (1*w) mod n=w mod n
加法逆元(-w):对于Zn中的任意w,存在一个z使得w+z同余0 mod n。
令a与n互素,如果(a*b)同余(a*c)(mod n),那么b同余c (mod n) 。
对于任何一般的模数n,如果a和n有任何公因子的话,用乘数a依次作用于0到n-1的所有整数将不会产生一个完整剩余类集。一般来说,如果一个整数与n互素,那么它在Zn中有一个乘法逆元。
给定一个素数p,元素个数为p的有限域GF(p)被定义为整数{0,1,…,p-1}的集合Zp,其运算为模p的算术运算。
摘自:https://blog.csdn.net/android_jiangjun/article/details/79886211