机器人走路问题
一个机器人可以在1~N上行走,每一步可以向前或向后走,给定起点S > 1,终点 < N,每一次行走K步,机器人从S走到E一共有多少种方法。
暴力递归

暴力递归存在大量重复的递归过程。可以用空间换取时间,记录可能出现的重复解,之后不需要递归展开直接拿到之前算过的值。即,记忆化搜索。时间复杂度O(2^K)
1 public static int walkMethod(int N, int start, int end, int K){ 2 return process(N,start,end,K); 3 } 4 /** 5 * 6 * @param N 一共有N个位置 7 * @param cur 当前在哪个位置 8 * @param end 最终的目标位置 9 * @param restK 可以走几步 10 * @return 11 */ 12 private static int process(int N, int cur, int end, int restK) { 13 if(restK == 0){//不能继续走了 14 return cur == end? 1:0;//找到1种 或者 没找到 15 } 16 if(cur == 1){//只有一种走法 向右走 17 return process(N,2,end,restK-1); 18 } 19 if(cur == N){//只有一种走法 向左走 20 return process(N,N-1,end,restK-1); 21 } 22 //可以向左走 或者 向右走 23 return process(N,cur-1,end,restK-1) + 24 process(N,cur+1,end,restK-1); 25 }
记忆化搜索
时间复杂度O(K*N)
1 public static int walkMethod2(int N, int start, int end, int K) { 2 int dp[][] = new int[K + 1][N + 1]; 3 for (int i = 1; i <= K; i++) { 4 for (int j = 0; j <= N; j++) { 5 dp[i][j] = -1; 6 } 7 } 8 return process2(N, start, end, K, dp); 9 } 10 11 private static int process2(int N, int cur, int end, int restK, int[][] dp) { 12 if (dp[restK][cur] != -1) { 13 return dp[restK][cur];//之前计算过 直接return 14 } 15 if (restK == 0) { 16 dp[restK][cur] = cur == end ? 1 : 0; 17 return dp[restK][cur]; 18 } 19 if (cur == 1) { 20 dp[restK][cur] = process2(N, cur + 1, end, restK - 1, dp); 21 }else if (cur == N) { 22 dp[restK][cur] = process2(N, cur - 1, end, restK - 1, dp); 23 }else{ 24 dp[restK][cur] = process2(N, cur - 1, end, restK - 1, dp) + process2(N, cur + 1, end, restK - 1, dp); 25 } 26 return dp[restK][cur]; 27 }
严格表结构
表的含义是:restK步走到cur有f(restK, cur)种方法
从开始 2 走到 终点 4 【f(0,4) = 1 f(0,else) = 0】走4步有多少种方法
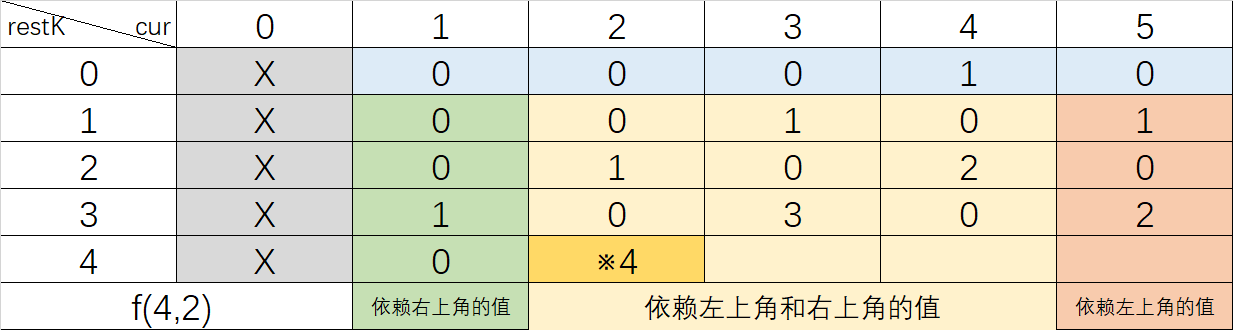
dp(restK, cur) = dp(restK-1, cur-1) 【cur == N】
dp(restK, cur) = dp(restK+1, cur-1) 【cur == 1】
dp(restK, cur) = dp(restK-1, cur-1) + dp(restK+1, cur-1) 【1<cur<N】
return dp(K, start)