树链剖分学习笔记

树链剖分，就是将一颗树分成若干个编号连续的链,将树上问题转换为线性问题,降低问题的处理难度。

模板题:P3384 【模板】轻重链剖分

题目描述

给一颗节点数为(n)的带点权树,有以下几种操作:

• 将树从 (x) 到 (y) 结点最短路径上所有节点的值都加上 (z)

• 求从 (x) 到 (y) 节点最短路径上的所有 节点值之和

• 以 (x) 为根节点的子树内所有节点值都加上 (z)。

• 求以 (x) 为根节点的子树内所有节点值之和

数据范围:(1le Nle10^5)

一些定义

• 重儿子：以一个非叶子节点中的一个儿子为根的子树最大的那一个儿子称为重儿子

• 轻儿子：一个非叶子节点中除了重儿子以外的儿子

• 重边：结点与其重儿子的边称为重边

• 轻边：结点与其轻儿子的边称为轻边

• 重链：由重边组成的路径

• 轻链：由轻边组成的路径

算法流程

首先是两次(DFS)

第一次求出子树大小,父节点,深度,重儿子这些之后要用的东西

void dfs1(int u,int f,int deep){
	dep[u] = deep;//深度
	fa[u] = f;//父亲节点
	size[u] = 1;//初始化子树大小
	int maxson = -1;
	for(int i=head[u];i;i = e[i].next){
		int v = e[i].v;
		if(v==f) continue;
		dfs1(v,u,deep+1);
		size[u]+=size[v];
	    if(size[v]>maxson) son[u] = v,maxson = size[v];//重儿子
	}
	
}

第二次(dfs)则是将树上的节点重新编号,划分成若干条链

每次都去选取自己的重儿子进行连接,这样可以尽可能的让一条链够长

其余的轻儿子则作为另一条链的开头

画成图的话大概是这样:

(ps:图中的红色节点均为重儿子)

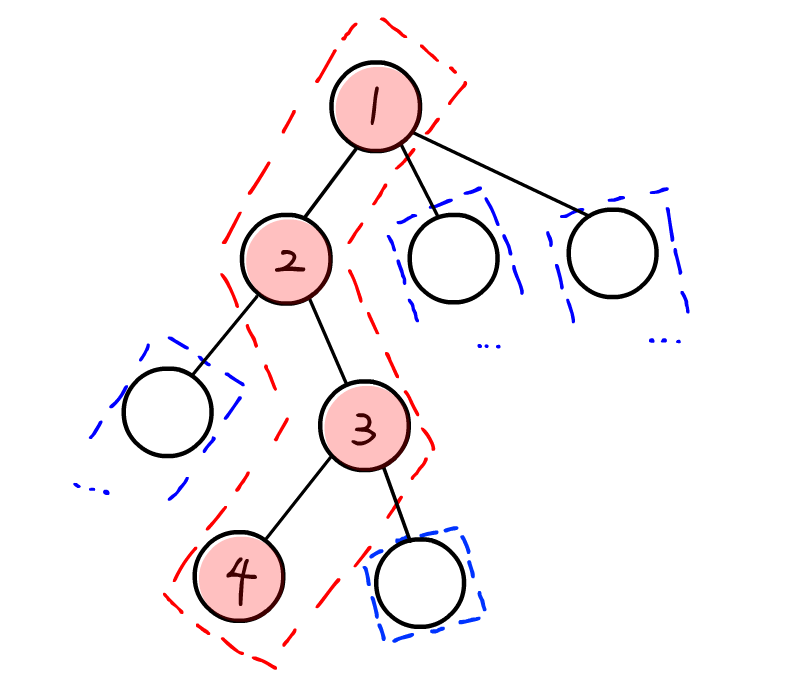
代码:

void dfs2(int u,int topf){//topf为一条链的头
	id[u] = ++tot;//重新编号,赋值
	val[tot] = w[u];
	top[u] = topf;//记录链头,之后有用
	if(!son[u]) return;//为叶子节点
	dfs2(son[u],topf);//以重儿子向下继续连接
	for(int i=head[u];i;i=e[i].next){//
		int v = e[i].v;
		if(v==fa[u]||v==son[u]) continue;
		dfs2(v,v);其余的边则作为新一条链的开头
	}
}

使用线段树维护这些链

对于操作1跟操作2

每次查询和修改从u到v的路径时

只需将低的那个点跳到上条链的结尾,也就是自己所在的链的头的父节点,同时查询/修改跳过的这段链的值即可

int qb(int u,int v){
	int ans = 0;//操作1~5
	while(top[u]!=top[v]){//如果不在同一条链上
		if(dep[top[u]]<dep[top[v]]) swap(u,v);//跳高度低的那个
		ans+=query(1,1,n,id[top[u]],id[u]);//查询该端的值,修改也同理
		ans%=mo;
		u = fa[top[u]];//跳到链头的父节点
	}
	if(dep[u]>dep[v]) swap(u,v);
	ans+=query(1,1,n,id[u],id[v]);//操作6
	ans%=mo;
	return ans;
}

对于操作(3,4),由于是(dfs),其子树的编号也一定是连续的

直接查询/修改区间([id[u],id[u]+size[u]-1])即可

((id[u])为该节点重组后的编号,(size[u])为子树大小)

代码:

#include<bits/stdc++.h>
using namespace std;
#define lson (node<<1)
#define rson (node<<1|1)
#define mid ((l+r)>>1)
#define len (r-l+1)
const int MAXN = 200000+10;
struct e{
	int u,v,next;
}edge[MAXN<<1];
int w[MAXN<<2];
int n,m,mo;
int head[MAXN<<2],cnt = 1;
int dep[MAXN],fa[MAXN],son[MAXN],size[MAXN];
int id[MAXN],val[MAXN],top[MAXN];
void add(int u,int v){
	edge[cnt].u=u;
    edge[cnt].v=v;
    edge[cnt].next=head[u];
    head[u]=cnt++;
}


void dfs1(int x,int f,int deep){
	dep[x] = deep;
	fa[x] = f;
	size[x] = 1;
	int maxson = -1;
	for(int i=head[x];i;i=edge[i].next){
		int v= edge[i].v;
		if(v==f) continue;
		dfs1(v,x,deep+1);
		size[x]+=size[v];
		if(size[v]>maxson) son[x] = v,maxson = size[v];
	}
}
int tot = 0;
void dfs2(int x,int topf){
	id[x] = ++tot;
	val[tot] = w[x];
	top[x] = topf;
	if(!son[x]) return;
	dfs2(son[x],topf);
	for(int i=head[x];i;i=edge[i].next){
		int v = edge[i].v;
		if(v==fa[x]||v==son[x]) continue;
		dfs2(v,v);
	}
}


struct st{
	int sum;
	int tag;
}tree[MAXN<<2];

void pushup(int node){
	tree[node].sum = (tree[lson].sum + tree[rson].sum)%mo;
}
void build(int node,int l,int r){

	if(l==r){
		tree[node].sum = val[l];
		if(tree[node].sum>mo) tree[node].sum%=mo;
		return;
	}
	build(lson,l,mid);
	build(rson,mid+1,r);
	pushup(node);
}
void pushdown(int node,int l,int r){
	if(tree[node].tag==0) return;
    tree[lson].tag+=tree[node].tag;
    tree[rson].tag+=tree[node].tag;
    tree[lson].sum+=tree[node].tag*(len-(len>>1));
    tree[rson].sum+=tree[node].tag*(len>>1);
    tree[lson].tag%=mo;
    tree[rson].tag%=mo;
	tree[lson].sum%=mo;
	tree[rson].sum%=mo;
	tree[node].tag = 0; 
}
void change(int node,int l,int r,int x,int y,int k){
	if(x<=l&&r<=y){
		tree[node].tag+=k;
		tree[node].sum+=k*(r-l+1);
		tree[node].tag%=mo;
		tree[node].sum%=mo;
		return;
	}
	pushdown(node,l,r);
	if(x<=mid) change(lson,l,mid,x,y,k);
	if(y>mid) change(rson,mid+1,r,x,y,k);
	pushup(node);
}
int query(int node,int l,int r,int x,int y){
	
	if(x<=l&&r<=y){
		return tree[node].sum%mo;
	}
	pushdown(node,l,r);
	int res = 0;
	if(x<=mid) res+=query(lson,l,mid,x,y);
	if(y>mid) res+=query(rson,mid+1,r,x,y);
	res%=mo;
	return res%mo;
}


void test(int node,int l,int r){
	cout<<tree[node].sum<<"  "<<tree[node].tag<<endl;
	if(l==r) return;
    test(lson,l,mid);
    test(rson,mid+1,r);
    return;
}
int qb(int u,int v){
	int ans = 0;
	while(top[u]!=top[v]){
		if(dep[top[u]]<dep[top[v]]) swap(u,v);
		ans+=query(1,1,n,id[top[u]],id[u]);
		ans%=mo;
		u = fa[top[u]];
	}
	if(dep[u]>dep[v]) swap(u,v);
	ans+=query(1,1,n,id[u],id[v]);
	ans%=mo;
	return ans;
}
void ub(int u,int v,int k){
	while(top[u]!=top[v]){
		if(dep[top[u]]<dep[top[v]]) swap(u,v);
		change(1,1,n,id[top[u]],id[u],k);
		u = fa[top[u]];
	}
	if(dep[u]>dep[v]) swap(u,v);
	change(1,1,n,id[u],id[v],k);
}
int main(){
	int root;
    scanf("%d%d%d%d",&n,&m,&root,&mo);
    for(int i=1;i<=n;i++) scanf("%d",&w[i]);
    for(int i=1;i<n;i++){
    	int u,v;
    	scanf("%d%d",&u,&v);
    	add(u,v);
    	add(v,u);
	}
	dfs1(root,0,1);
	dfs2(root,root);
	for(int i=1;i<=n;i++){
		cout<<dep[i]<<"  "<<val[i]<<"  "<<size[i]<<endl;
	}
	build(1,1,n);
	while(m--){
		int k,x,y,z;
		scanf("%d",&k);
		if(k==1){
			scanf("%d%d%d",&x,&y,&z);
			ub(x,y,z);
		}
		else if(k==2){
			scanf("%d%d",&x,&y);
			printf("%d
",qb(x,y));
		}
		else if(k==3){
			scanf("%d%d",&x,&y);
			change(1,1,n,id[x],id[x]+size[x]-1,y);
		}
		else{
			scanf("%d",&x);
			printf("%d
",query(1,1,n,id[x],id[x]+size[x]-1)%mo);
		}
	}
}

话说树剖的好多题都好裸啊