今天是钟皓曦老师的讲授~
今天的题比昨天的难好多,呜~
T1


我们需要找到一个能量传递最多的异构体就好了;
整体答案由花时间最多的异构体决定;
现在的问题就是这么确定一个异构体在花费时间最优的情况下所花的时间是多少;
我们去枚举一个异构体 i,以这个异构体为分界线将其分成左右两部分,设左半部分的异构体的能量和为 sum;

如果 sum > ( i-1 ) * v,v * n - sum(右部分) < 0 ,说明左边的能量是够的,不需要再输入能量了,但是右部分却不够,所以我们需要从左边往右边输送能量,那么输送的能量的多少就是 i 这个异构体的贡献;
做法:去枚举每一个 i,考虑这个节点它的作用(往哪里传递能量) ,注意一共四种情况:
1. 左边多,右边少;那么 i 节点的作用就是把左边多余的能量传递到右边;
2. 左边少,右边多;那么 i 节点的左右就是把右边多余的能量传递到左边;
3. 左边多,右边也多;也就是说 i 这个点少了好多能量,我们就要把两边多余的能量搬到 i,时间取决于耗时长的一遍:max(x,y);
4. 左边少,右边也少;也就是说 i 这个点多了好多能量,我们要把多余的能量搬到两边,但是注意每一时刻只能搬一点能量,所以需要 x+y 的时间;
所以这个题就做完了;
#include<cstdio> #include<cstdlib> #include<cstring> #include<algorithm> using namespace std; const int maxn=100010; int n,z[maxn]; long long sum[maxn]; void read() { scanf("%d",&n); for (int a=1;a<=n;a++) scanf("%d",&z[a]); } long long work() { for (int a=1;a<=n;a++) sum[a] = sum[a-1]+z[a]; if (sum[n]%n) return -1; long long ans=0,v=sum[n]/n; for (int a=1;a<=n;a++) { long long l=sum[a-1]-1ll*(a-1)*v; long long r=sum[n]-sum[a]-1ll*(n-a)*v; if (l<0 && r<0) ans=max(ans,-l-r); ans=max(ans,max(abs(l),abs(r))); } return ans; } int main() { read(); printf("%lld ",work()); return 0; }
T2

语文太差了,还以为必须要从 1 走到 n,然后 100 -> 0(其实是玄学 RE);
没要求必须从左往右走?炸了~
我们从小到大排好序,这样的话我们选数的时候只需要考虑所选的数是不是前面的数的倍数就行了(因为前面的数一定是更前面所有数的倍数);
f [ i ] 表示已经取了第 i 个数了,我们去枚举前面选的那个数是多少,看是不是它的倍数就可以了:
f [ i ] = max ( f [ j ] ) + 1,a [ i ] 是 a [ j ] 的倍数;
这个题搜索写得好好像可以过。。
我们看到有个很重要的隐藏 bug:有 20% 的数据保证所有城市的数都不重复;
考虑到由于所选的数都是倍数关系,所以这些城市的数最多就 20 个不同的数!
那么我们可以先去重,然后如果一个数 a [ i ] 被选上了,那么和它相等的数也都要选上,这样才能保证最优嘛;
所以我们可以在此基础上搜索,或者按照上面说的那样 dp 一下,就可以过了;
然而不是正解?
正解:
我们可以开一个桶,记录每个数出现了多少次;
改造一下 dp:f [ i ] 我取出来的序列最后一个数等于 i 的情况下最长是多少;
那么接下来我们要取得的是 i 的倍数,所以我们就去枚举 i 的倍数,一直枚举到一百万就行了;
f [ k * i ] = max ( f [ i ] + cnt [ k * i ] );
我们不关心那个数是多少,我们只关心有多少个 。
#include<cstdio> #include<cstdlib> #include<cstring> using namespace std; const int maxn=1000010; int n,cnt[maxn],f[maxn]; int main() { scanf("%d",&n); for (int a=1;a<=n;a++) { int v; scanf("%d",&v); cnt[v]++; f[v]++; } int ans=0; for (int a=1;a<=1000000;a++) if (f[a]) { if (f[a]>ans) ans=f[a]; for (int b=a+a;b<=1000000;b+=a) if (cnt[b] && f[a]+cnt[b]>f[b]) f[b]=f[a]+cnt[b]; } printf("%d ",ans); return 0; }
T3

zhx:明天考试不考 2-SAT,真香~
最小值最大化,我们用二分;
我们二分答案 v,那么我们所选的任意两张卡牌的差值的绝对值都要大于 v;
假如我们有两组卡牌,他们的战斗力分别是 a1 , b1 和 a2 , b2 ;
如果 a1 - a2 < v,那么说明 a1 和 a2 不能同时选,所以如果我们选了 a1 ,那么我们就只能选 b2 了,从 a1 向 b2 ;
这样能过 50% 的数据;
考虑到建边的时间复杂度是 O ( n2 ) 的,显然过不了 100% 的数据;
线段树优化建边 。
我们将这 2n 个数从小到大排序,假如现在我们考虑 ci ,需要和它建边的点一定是一个连续的区间;
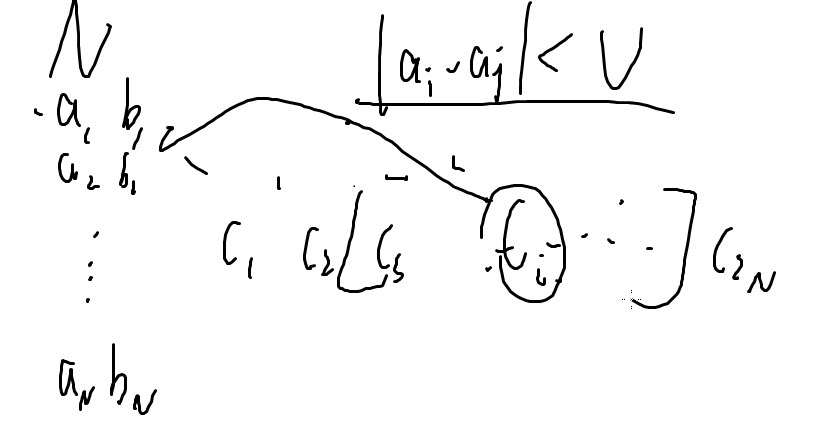
发现这是一个区间加边的操作,怎么搞呢?
我们建一棵线段树,然后对线段树进行区间加边的操作,我们可以把线段树上的边也看做是图的一部分的话,那么我们就只需要建 log n 条边:
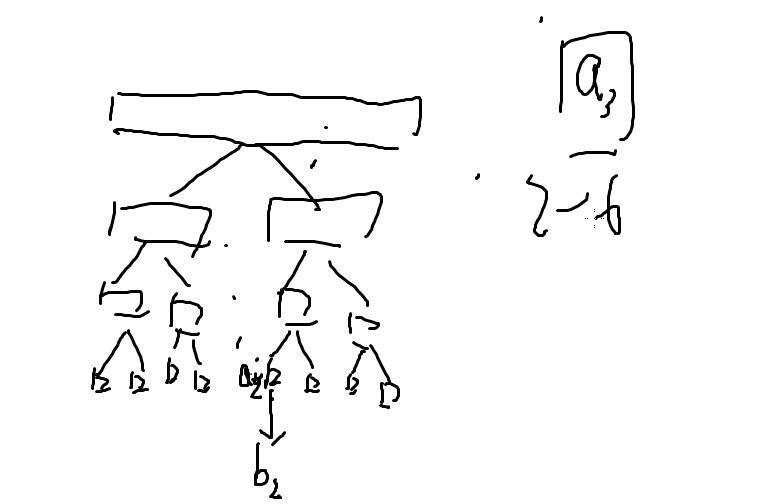
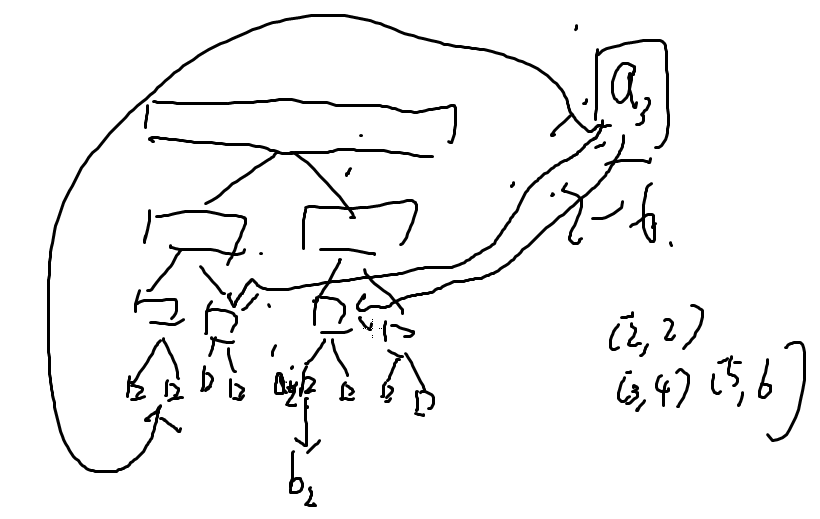
每次只需要加 log n 条边,总时间复杂度 O ( n log 2 n );
#include<cstdio> #include<cstdlib> #include<cstring> #include<cctype> #include<algorithm> using namespace std; const int BUF_SIZE = 30; char buf[BUF_SIZE], *buf_s = buf, *buf_t = buf + 1; #define PTR_NEXT() { buf_s ++; if (buf_s == buf_t) { buf_s = buf; buf_t = buf + fread(buf, 1, BUF_SIZE, stdin); } } #define readint(_n_) { while (*buf_s != '-' && !isdigit(*buf_s)) PTR_NEXT(); bool register _nega_ = false; if (*buf_s == '-') { _nega_ = true; PTR_NEXT(); } int register _x_ = 0; while (isdigit(*buf_s)) { _x_ = _x_ * 10 + *buf_s - '0'; PTR_NEXT(); } if (_nega_) _x_ = -_x_; (_n_) = (_x_); } #define readstr(_s_) { while (!isupper(*buf_s)) PTR_NEXT(); char register *_ptr_ = (_s_); while (isupper(*buf_s) || *buf_s == '-') { *(_ptr_ ++) = *buf_s; PTR_NEXT(); } (*_ptr_) = '�'; } #define readlonglong(_n_) { while (*buf_s != '-' && !isdigit(*buf_s)) PTR_NEXT(); bool register _nega_ = false; if (*buf_s == '-') { _nega_ = true; PTR_NEXT(); } long long register _x_ = 0; while (isdigit(*buf_s)) { _x_ = _x_ * 10 + *buf_s - '0'; PTR_NEXT(); } if (_nega_) _x_ = -_x_; (_n_) = (_x_); } #define wmt 1,(n<<1),1 #define lson l,m,rt<<1 #define rson m+1,r,rt<<1|1 const int maxn=100010; const int maxp=maxn+(maxn<<2); const int maxm=maxn+maxp+maxn*20; int n,size,cnt,en,t,dfn[maxp],low[maxp],s[maxp],belong[maxp],pos[maxn]; bool instack[maxp]; struct edge { int e; edge *next; }*v[maxp],ed[maxm]; void add_edge(int s,int e) { en++; ed[en].next=v[s];v[s]=ed+en;v[s]->e=e; } struct rec { int v,p; rec(){} rec(int a,int b) { v=a;p=b; } }z[maxn]; bool operator<(const rec &a,const rec &b) { return a.v<b.v; } void dfs(int p) { t++; dfn[p]=low[p]=t; instack[p]=true; s[++size]=p; for (edge *e=v[p];e;e=e->next) if (!dfn[e->e]) { dfs(e->e); low[p]=min(low[p],low[e->e]); } else { if (instack[e->e]) low[p]=min(low[p],dfn[e->e]); } if (dfn[p]==low[p]) { cnt++; while (s[size]!=p) { belong[s[size]]=cnt; instack[s[size]]=false; size--; } belong[p]=cnt; instack[p]=false; size--; } } void build(int l,int r,int rt) { if (l==r) { add_edge(rt+(n<<1),z[l].p<=n?z[l].p+n:z[l].p-n); return; } int m=(l+r)>>1; build(lson); build(rson); add_edge(rt+(n<<1),(rt<<1)+(n<<1)); add_edge(rt+(n<<1),(rt<<1|1)+(n<<1)); } void insert(int l,int r,int rt,int nowl,int nowr,int p) { if (nowl<=l && r<=nowr) { add_edge(p,rt+(n<<1)); return; } int m=(l+r)>>1; if (nowl<=m) insert(lson,nowl,nowr,p); if (m<nowr) insert(rson,nowl,nowr,p); } bool check(int k) { en=0;cnt=0; memset(v,0,sizeof(v)); memset(dfn,0,sizeof(dfn)); build(wmt); int r=1,l=1; for (int a=1;a<=(n<<1);a++) { int op,p=z[a].p; if (p<=n) op=pos[p+n]; else op=pos[p-n]; while (r<=a && z[r].v <= z[a].v-k) r++; if (r<a && r>=1 && z[r].v > z[a].v-k) { if (op>=r && op<=a-1) { if (op>r) insert(wmt,r,op-1,z[a].p); if (op<a-1) insert(wmt,op+1,a-1,z[a].p); } else insert(wmt,r,a-1,z[a].p); } while (l<=(n<<1) && z[l].v < z[a].v+k) l++; l--; if (l>a && l<=(n<<1) && z[l].v < z[a].v+k) { if (op>=a+1 && op<=l) { if (op>a+1) insert(wmt,a+1,op-1,z[a].p); if (op<l) insert(wmt,op+1,l,z[a].p); } else insert(wmt,a+1,l,z[a].p); } } for (int a=1;a<=(n<<1);a++) if (!dfn[a]) dfs(a); for (int a=1;a<=n;a++) if (belong[a]==belong[a+n]) return false; return true; } int main() { readint(n); int minv=0x3f3f3f3f,maxv=-0x3f3f3f3f; int x=0; for (int a=1;a<=n;a++) { int v1,v2; readint(v1); readint(v2); z[++x]=rec(v1,a); z[++x]=rec(v2,a+n); minv=min(minv,min(v1,v2)); maxv=max(maxv,max(v1,v2)); } if (maxv-minv+1 < n) { printf("0 "); return 0; } sort(z+1,z+x+1); for (int a=1;a<=(n<<1);a++) pos[z[a].p]=a; int l=0,r=1000000001; while (l+1!=r) { int m=(l+r)>>1; if (check(m)) l=m; else r=m; } printf("%d ",l); return 0; }

f [ i ][ j ]:表示第 i 位到第 j 位所能组成的最长回文子序列;
考虑怎么使序列更长?我们分别在两端加一个相同的字符不就好了?
所以我们枚举 i 之前,j 之后找一个相同的字符就好了;
f [ i ][ j ] +1 -> f [ k ][ l ];
时间复杂度 O(n4)
考虑到 dp 有三种写法:
1. 自己算别人;
2. 别人算自己;
3. 记忆化搜索;
我们刚刚的写法是自己去算别人,现在我们来考虑用别人算自己;
如果用第 i 个字符:f [ i+1 ][ j ];
如果用第 j 个字符:f [ i ][ j-1 ];
如果第 i 个字符和第 j 个字符我们都用:f [ i+1 ][ j-1 ];
那么转移就是:f [ i ][ j ] = max ( f [ i+1 ][ j ] , f [ i ][ j-1 ] , f [ i+1 ][ j-1 ] ) ,s [ i ] == s [ j ];
zhx:我们发现这道题十分的水,所以来加强一下,问本质不同的回文字符串有多少个?
对于本质相同:aba 类型算一种:121,252,707……;

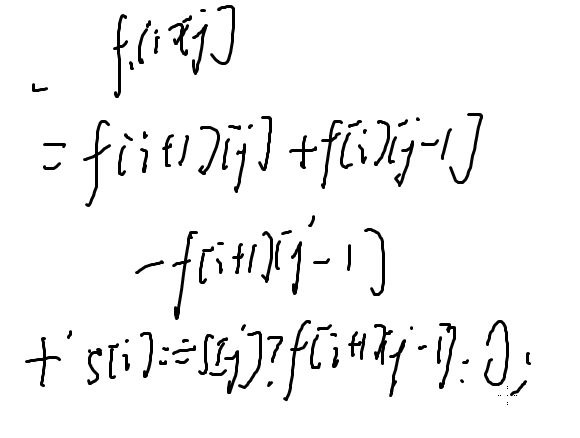

f [ k+1 ][ l-1 ] 内的字符串都会被重新再算一次;
所以我们只需要再从答案里减去 f [ k+1 ][ l-1 ] 就行了;
k 和 l 的位置可以预处理;
整体复杂度 O(n2);

做排列类型的 dp 题时,我们考虑把数从小到大一个一个插进去;
排列的性质:
我们随便从排列里取出一个前缀,它还是个排列;
f [ i ][ j ]:我们已经用 1~i 将前 i 个位置填好了,第 i 个位置是 j 的方案数是多少;
转移:f [ i ][ j ] -> f [ i+1 ][ k ]
分两组情况:
1. ai > ai+1 ,也就是说我们接下来插的这个数比之前插的数要小:
那么我们能填的数就是 1 ~ j-1(前一个填的数是 j),但是显然我们要填的这个数必然在前面已经用过了,会发生冲突,怎么办呢?
我们把 1~i 中大于等于 k 的数全部 +1 就好:
假如我们第六位插入一个 3,发现小于前一个插入的 5,那么我们让前面所有大于等于 3 的数全部加一,这样就空出一个 3 来了:
2 3 4 1 5
2 4 5 1 6 3;
2. ai < ai+1 ;
道理是一样的,我们所插入的数的范围就变成了:j < k <= i+1(要大于前面插入的那个数,同时要在 i+1 以内)
转移方程:
1. ai > ai+1 :f [ i+1 ][ k ] = f [ i ][ j ] (k < j)
2. ai < ai+1 :f [ i+1 ][ k ] = f [ i ][ j ] (j < k <= i+1 )
时间复杂度:O ( n3 );
考虑到加一的时候我们可以前缀和优化,所以就优化成了 O ( n2 );

日常盲设状态:f [ i ][ j ] 表示选了 i 个点到了第 j 层的方案数;
发现这个状态没有办法转移。。。那怎么办呢?
换一个状态:f [ i ][ j ] :表示已经用了 i 个点,它们的深度都小于等于 j 的方案数;
答案就是:f [ n ][ n ] - f [ n ][ k-1 ];
考虑转移:
我们考虑拆根,去枚举左右结点个数:
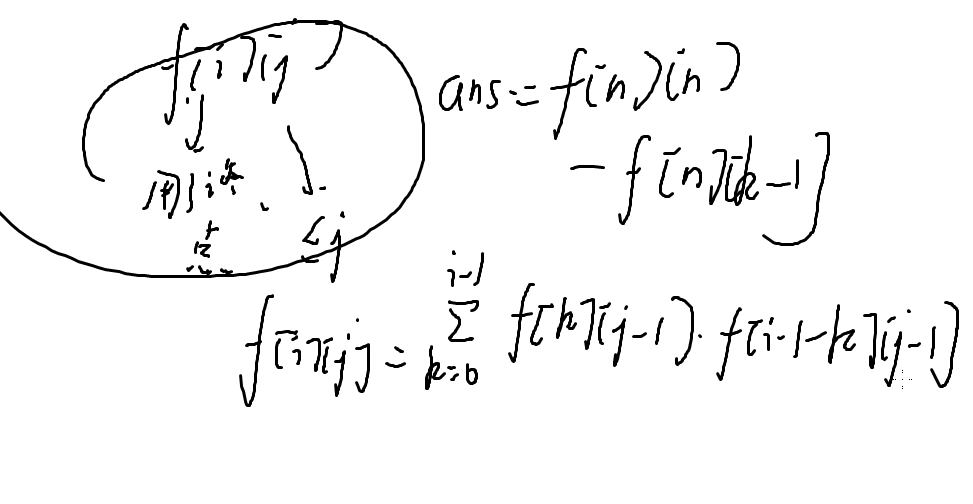

有两种可能的答案:
[ i,i,i ] ,[ i-1,i,i+2 ]
对于第二种情况,如果出现了超过 2 个的情况,我们完全可以将它们拆成第一种的情况,所以第二种的数量一定是不超过 2 个的;
状态:
f [ i ][ j ][ k ] 我们已经处理完了 1~ i 这些数,用了 j 个 i-1,i,i+1,k 个 i,i+1,i+2 的方案数,注意 j 和 k 一定是小于等于 2 的;
转移:
用 l 个 i+1,i+2,i+3;
然后咕咕咕了qwq~

f [ i ][ j ][ k ]:表示在 i 轮结束之后,aj < ak 的方案数,j < k;
Σ ( j >k ) f [ q ][ j ][ k ];
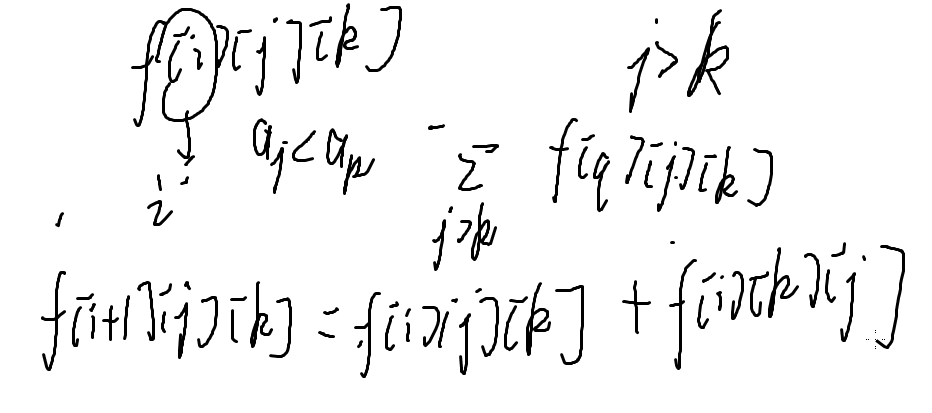
但是交换 j,k 两个位置不仅仅是影响这两个位置的值,还会对后面的位置产生影响;
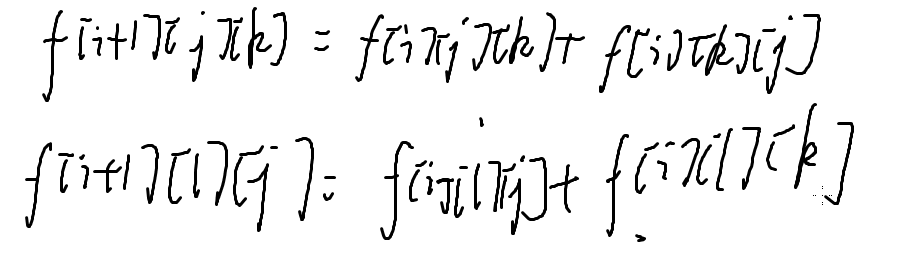
时间复杂度 O(n2);
对拍讲解现场:
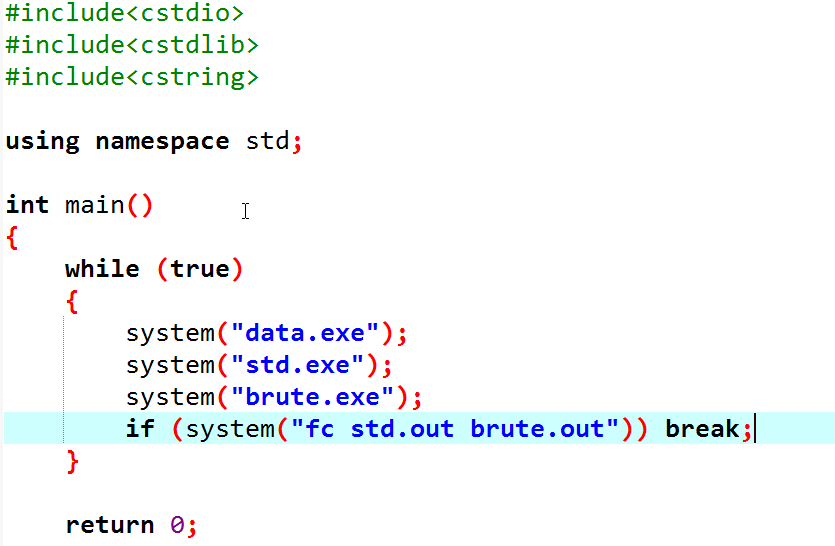

随机生成树:

扫把图:

zhx AK做题方法:
前 10~ 15 分钟全部用来读题,包含手推样例;
然后我们选择一个合理的做题的顺序,一般来说是 1,2,3 的顺序,但是也不一定嘛qwq;
先写暴力,拿到保底分;
然后朝着 100 分的方向前进;
最后 15 分钟一定要丢掉键盘,静坐待亡检查一下自己有没有zz(数组开大开小,文件输入输出……)!

