当天走得太兴奋了,忘记保存就关电脑了o(╥﹏╥)o,现在补上( p′︵‵。)
今天是杨思祺老师的讲授~
练习题

首先求出最短路;
如果选择的边不是最短路上的边,那么毫无影响;
对于最短路径上的边,我们需要枚举路径上每条边,加倍再跑 Dijkstra。

我们可以考虑在建图方面进行改造:
假设我们建完图之后是长这个样子的:
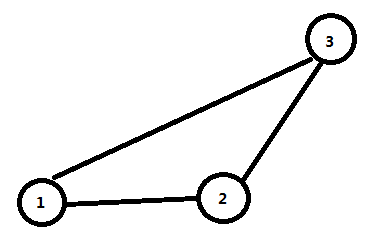
我们先考虑 k=1 的情况,也就是我们可以使一条边的权值变为0。
我们可以将这个图在上层拷贝一份,将每个结点从上层的能到达的结点连一条有向边,这些边的权值为0,这样就实现了删除一条边的效果:
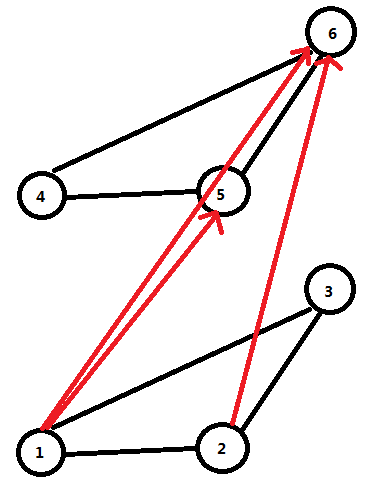
那么怎么设置上层点的编号呢?
我们可以像棋盘一样设置:
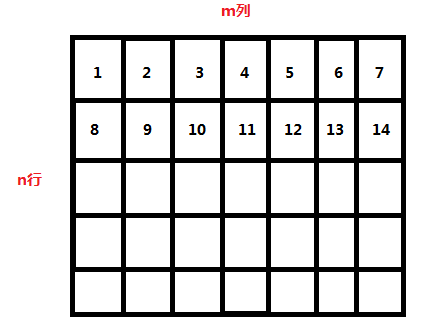
假设我们有个 n × m 的棋盘,那么这个棋盘上第 k 行第 j 列的数就是:(k-1)* m + j;
那么我们也可以根据这个规律来给上层的图的结点编号:(2-1)* n + j;
那么最终的答案就是:1 -> 6 的最短路,一遍Dijkstra 即可;
分析完上面 k=1 的情况后,我们就可以得出删除 k 条边的做法了:
我们拷贝 k 层图,按照上面的思路连权值为0的有向边,那么最后的答案就是:1 -> (k-1)* n 点的最短路;
但是考虑到可能用不了 k 次更新(比如本来就不够 k 条边),所以我们再从分层图的每一层的点向下一层的对应点连一条边,表示白白浪费一次更新机会~
我们这样建边实现边的跳跃。
分层图的实现:通过映射,将二维图转化为一维图;

n2 建边,但是发现会有许多边是冗余的。
我们先按照 x 从小到大排好序;
假如平面内有三个点(x1,y1),(x2,y2),(x3,y3);
第一个点到第三个点的直接路径为:min(| x1- x3 |,| y1- y3 |)= x3 - x1;
我们也可以考虑从中转点第二个点来走到第三个点:min(| x1- x2 |,| y1- y2 |)+ min(| x2- x3 |,| y2- y3 |)= x2 - x1 + x3 - x2 = x3 - x1;
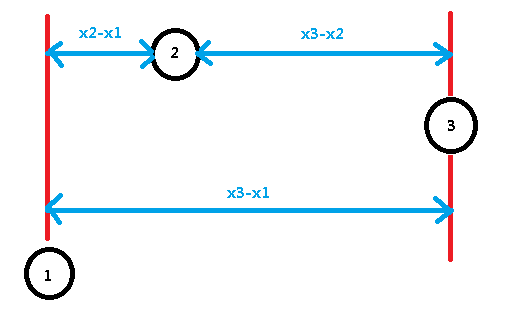
如果我们按照 x 排好序后,那么点 1 到点 3 的 x 距离完全可以用点 1 到点 2 + 点 2 到点 3 的 x 距离来表示;
也就是说,我们按照 x 排序后只需要在相邻两个点连一条边就好了;
对于 y 的话是一样的 。

我们尽量让最小边最大,但是这样操作会使最大边的选择范围变小,可能会导致最大边变大;
我们从大到小枚举最小边,用更大的边做 Kruskal,当 S 和 T 连通立即 break。
LCT,从大到小加边维护最小生成树。

1. 二分做法:
我们二分枚举 mid,小于 mid 的边连部落内部,大于等于 mid 的边是部落间的距离,看看是否连成了至少 k 个连通块即可 。
2. 最小生成树:
我们按照 Kruskal 的做法,当我们选中了 n-k 条边的时候,也就意味着此时有 k 个联通块,那么我们只需要再找一条不是部落间的边就是答案了,也就是选中的第 n-k+1 条边 。
我们需要求出每个杯子的奇偶性,才能知道答案,也就是要求每个 [ 0 , i ] 的奇偶性,就像前缀和一样,干脆直接用 S [ i ] 来表示区间 [ 0 , i ] 的奇偶性;
假如我们知道了区间 [ l , r ] 的奇偶性,那么我们就是知道了 S [ r ] - S [ l-1 ] 的奇偶性了;
奇偶性的转化:假如我们知道了 [ l , k ] 的奇偶性了,又知道了 [ k+1 , r ] 的奇偶性,那么我们也就知道了 [ l , r ] 的奇偶性!
我们发现这一点和树上唯一路径很像:知道了 x -> y 的路径,又知道了 y -> z 的路径,也就知道了 x -> z 的路径 。
那么通过这一条很重要的性质,我们求每个前缀和的话,其实就是求 0 都能走到每个点的最小花费和,再具体一点就是求最小代价使得整个图联通,直接最小生成树板子!

在任意一个非加油站点,不论目的地是哪个加油站,先前往最近 的加油站再前往目的地是最优策略。
加油站之间存在一种边,可以视为一条由非加油站点串起来的路径。我们希望找到加油站之间的最小生成树。
多源最短路,以所有加油站为起点,记录下每个点到最近加油站的距离,以及是哪个加油站。
建立用于做最小生成树之间的边:如果一条边 < u, v > 满足 u 和 v 的最近加油站不同,则 disu + disv + wu,v 构成一条 fromu 和 fromv 的边。 MST 算法求出最小生成树,倍增或树链剖分维护链上最小值。

记四个关键点为 E1,E2,W1,W2。
一条边 < u, v, w > 在从 S 到 T 的最短路上,当且仅当 DS,u + w + Dv,T Du,v。 找出所有同时在 E1 到 E2 和 W1 到 W2 最短路上的有向边,一 定无环形成 DAG。 拓扑排序求 DAG 最长路。 注意:对于同时在 E1 到 E2 和 W2 到 W1 最短路上的有向边再做一次。

设 a [1] 是最小的,在模 a [1] 意义下,0 到 a [1] − 1 每个位置都 有其最小可被表示值。
而如果 k 是可被表示的,那么 k + a [1], k + 2 × a [1], . . . 都可被表示。
故问题转化为求解每个位置最小可被表示数字。 建立 a[1] 个点,对于每个 a [ j ],j , 1,我们理解为可以花费 a [ j ] 代价从 x 点转移到 ( x + a [ j ] ) mod a [1] 点。建边之后从0 号点出发做单源最短路即可。