今天是赵和旭老师的讲授~
动态规划
动态规划的基本思想
利用最优化原理把多阶段过程转化为一系列单阶段问题,利用各阶段之间的关系,逐个求解。
更具体的,假设我们可以计算出小问题的最优解,那么我们凭借此可以推出大问题的最优解,进而我们又可以推出更大问题的最优解。(要满足最优子结构)
(从小问题答案推到大问题的答案)
而最小的问题也就是边界情况我们可以直接计算出答案来。
基本思想是将待求解的问题划归为若干个子问题(阶段),按顺序求解子阶段,小的子问题的解,为更大子问题的求解提供了有用的信息。
由于动态规划解决的问题多数有重叠子问题这个特点,为减少重复计算,对每一个子问题只解一次。
从小问题求出大问题,有点像分治。
但和分治又不同:分治没有重叠子问题,而动态规划不仅是把问题化小,而且可能化到同一个问题上,具有重叠子结构的性质;
动态规划的状态
动态规划过程中,需要有状态表示和最优化值(方案值)。
状态表示:是对当前子问题的解的局面集合的一种(充分的)描述。
最优化值:则是对应的状态集合下的最优化信息(方案值),我们最终能通过其直接或间接得到答案。
动态规划主要也就两个步骤:
1. 如何设计状态;
对于状态的表示,要满足三条性质
1:具有最优化子结构:即问题的最优解能有效地从问题的子问题的最优解构造而来。
2:能够全面的描述一个局面。一个局面有一个答案,而这个局面是需要一些参数来描述的。
3:同时具有简洁性:尽可能的简化状态的表示,以获得更优的时间复杂度。
设计状态的关键就是 充分描述,尽量简洁。
2. 如何进行状态转移;
由于具有最优化子结构(在最优化问题中),所以求当前状态的最优值可以通过其他的(较小的问题)状态的最优值加以变化而求出。所以,当一个状态的所有子结构都已经被计算之后,我们就可以通过一个过程计算出他的最优值。这个过程就是状态的转移。
注意:状态的转移需要满足要考虑到所有可能性。
怎么计算动态规划的时间复杂度?
一般简单动态规划时间复杂度 = 状态数 × 状态转移复杂度。
同时也就引出了 dp 的两种优化时间的方法
1:减少状态的维数。
2:加速状态转移,例如数据结构优化或者分析性质。
看个例题:

这是一道最为经典的完全用动态规划来解决的问题。
设 dp [ i ] 为以 a [ i ] 为末尾的最长上升子序列的长度。
最后的答案就是我枚举一下最长上升子序列的结束位置,然后取一个 dp [ i ] 最大值即可。
问题是如何求这个数组?
那我们回过头来想一想最开始说的动态规划的基本思想,从小的问题推出大的问题。
假设我们知道了dp[ 1 .. (i-1) ],我们怎么才能根据这些信息推出来 dp [ i ] 。
再次强化一下定义:dp [ i ] 表示以i结尾的最长上升子序列。
我们只需要枚举这个上升子序列倒数第二个数是什么就好了。
所以我们再枚举一下 a [ 1 ] ~ a [ i-1 ],找到一个 a [ k ] < a [ i ] && dp [ k ] 最大的 k,令 dp [ i ] = dp [ k ] + 1;
状态转移:dp [ i ] = max { dp [ j ] | a [ j ] < a [ i ] && j < i } +1 ;
之前的例子:
A:{2 , 5 , 3 , 4 , 1 , 7 , 6};
dp [ 1 ] = 1;
dp [ 2 ] = max { dp [ 1 ] } + 1;
dp [ 3 ] = max { dp [ 1 ] } + 1;
dp [ 4 ] = max { dp [ 1 ],dp [ 3 ] } + 1;
…… ……
时间复杂度 O(n2)。
套上之前的公式:状态数×状态转移复杂度。
状态数:dp [ 1..n ],只有n个状态。
状态转移:dp [ i ] = max { dp [ j ] | a [ j ] < a [ i ] && j < i } +1 ;
由于你每次都需要枚举之前的所有数,所以单次转移是O(n)。
所以总复杂度 O(n2)。
套上之前的公式:状态数 × 状态转移复杂度。
状态数:dp [ 1..n ],只有 n 个状态。
状态转移:dp [ i ] = max { dp [ j ] | a [ j ] < a [ i ] && j < i } +1 ;
由于你每次都需要枚举之前的所有数,所以单次转移是O(n)。
所以总复杂度 O(n2)。
在这个问题的分析中,突破口?
1:设计出了dp [ 1..n ] 这个可以储存以i结尾的子序列中最优的答案,这个状态表示。
2:通过分析问题成功能将当前状态的最优值能过由之前状态转移出来。dp [ i ] = max { dp [ j ] | a [ j ] < a [ i ] && j < i } +1 ,状态转移。
代码实现:


用 f[i][a] 表示前 i 位数包含 a 个乘号所能达到的最大乘积,我们只需要枚举上一个乘号所在的位置即可。
将 j 从 a 到 i-1 进行一次枚举,表示前 j 位中含有 a-1 个乘号,且最后一个乘号的位置在 j 处。那么当最后一个乘号在 j 处时最大值为前 j 位中含有 a - 1 个乘号的最大值乘上 j 处之后到 i 的数字。
因此得出了状态转移方程 f [ i ][ a ] = max ( f [ i ][ a ], f [ j ][ a-1 ] * cut ( j + 1,i ) )——(cut ( b + 1,i ) 表示 b + 1 到 i 位数字)
然后再写个高精度即可。
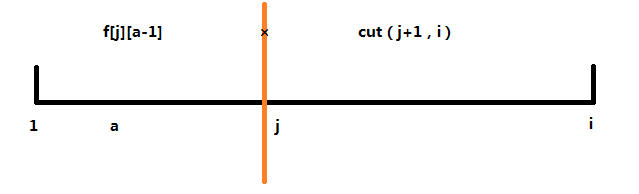
看图解释
先明确思路:
我们将 1~i 分成两部分,左半部分包含 a - 1 个乘号,有半部分没有乘号,分界线的位置也有一个乘号,所以我们去枚举分界线 j;
那么 j 枚举的范围是 a~i-1;

首先贪心的想,如果最终选出的一组挂饰,肯定是从上到下先挂所含挂钩多的,所以先按照挂钩数量从大到小排序。
状态设置:设 dp [ i ][ j ] 前 i 个挂饰,剩余 j 个挂钩的最大喜悦值是多少。
边界情况:如果没有挂钩就不能再放了,即 dp [ i ][ 0 ] 不能进行转移;
状态转移方程:
考虑第 i 个挂饰放不放即可。
如果挂上第 i 个挂钩,它会占据原先的一个挂钩,并产生 b [ i ] 个挂钩,即 dp [ i ][ j ] = dp [ i-1 ][ j + 1 - b [ i ] ] + a [ i ];
如果不挂的话,那么 dp [ i ][ j ] = dp [ i-1 ][ j ];
取 max 就做完了。
时间复杂度:O(n2);

我们设 f [ i ] 表示以i结尾的最长上升子序列长度。
我们设 g [ i ] 表示以i开头的最长下降子序列长度。
然后我们枚举哪一个为中心的最高点,f [ i ] + g [ i ] - 1 取最大值即可。
LIS 相关问题

一道二维偏序的题目~
如果我们按照 L 从大到小排序,那么问题就转化成求 W 的最少不上升序列数;
达沃斯定理:不上升子序列数 = 最长上升子序列的长度。(严格证明参考:dilworth 定理);
所以其实就是求一个最长上升子序列即可。
对 dp 优化的初探

两个 dp 优化方法:
1. 分析性质;
2. 数据结构优化;
LIS分析性质
状态转移:dp [ i ] = max { dp [ j ] | a [ j ] < a [ i ] && j < i } +1;
我们观察一下这个 dp 式子的转移,他到底是在做一个什么操作。
我们是找比 a [ i ] 小的 a [ j ] 里面,dp [ j ] 的最大值。
从这个角度不是很好优化,我们考虑另外一个思路,我们找最大的 k,满足存在 dp [ j ] == k && a [ j ] < a [ i ] 。
我们设 h [ k ] 表示 dp [ j ] == k 的所有 j 当中的最小的 a [ j ],就是说长度为 k 的最长上升序列,最后一个元素的最小值是多少,因为最后一个元素越小,肯定后面更容易再加上一个元素了。
然后我们发现了个奇妙的性质。
而 h [ k ] 肯定是单调不下降的;就是说“ 长度为k的最长上升序列最后一个元素的最小值 ” 一定是小于 “ 长度为 k+1 的最长上升序列最后一个元素的最小值 ”,如果不是的话,我们可以用后者所在上升子序列构造出一个更小的前者。
然后这个样子我们对于一个 a [ i ] 就可以找到,最大的 k,满足 h [ k ] 是小于 a [ i ] 的,然后 f [ i ] = k + 1。 找的过程是可以二分加速的。
然后同时在维护出h数组即可。
方法二:数据结构无脑暴力优化
数据结构不需要什么灵巧的闪光就是套路。
状态转移:dp [ i ] = max { dp [ j ] | a [ j ] < a [ i ] && j < i } +1 ;
我们把a [ j ] 看成坐标,dp [ j ] 看成权值,这就是每次求坐标小于等于某个值的权值最大值,然后每算完一个单点修改即可。
线段树能做,但是大材小用了。
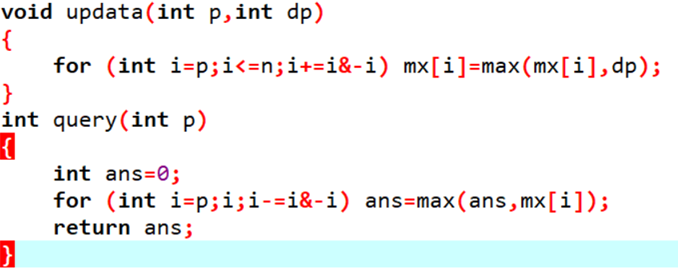
其实树状数组就可以解决。
LCS相关问题

我们设 dp [ i ] [ j ] 表示,S串的第 i 个前缀和 T 串的第 j 个前缀的最长公共子序列。
分情况:
如果S [ i ] == T [ j ],dp [ i ][ j ] = dp [ i-1 ][ j-1 ] + 1;
如果S [ i ] != T [ j ],dp [ i ][ j ] = max ( dp [ i-1 ][ j ],dp [ i ][ j-1 ] );
最后答案就是 dp [ n ][ m ] ;
对于 dp [ i ][ j ]:
如果,两个串最后一个位置相同,这两个位置一定在公共子序列中。
那么我们只需要求出S的 i-1 前缀和 T 的 j-1 前缀的最长上升子序列就可以了,而这个就是把问题化小。
如果最后一个位置不相同,那么两个位置一定不能匹配,所以肯定是另外两种情况选最大的。
几种 dp 的思考思路
大师:根据经验和直觉设计 dp 状态然后转移。
一般1:考虑结尾,分几种情况,发现可以转化为形式类似的子问题,根据这个类似的形式,设计状态。
(一般是只有一个结尾的问题我们这么考虑,对于多个结尾的(LIS),直接考虑一个分部即可。)
一般2:考虑搜索,然后转成记忆化再到递推:搜索 -> 记忆化搜索 -> 递归变递推。

其实这是一类套路,只不过这种套路可以考场上自己推出来,而不是由他人教。当然有些套路,比如网络流dinic算法怎么写,这个自己推就费劲了。但是这题是完全可以自己研究出来的。
我们设 dp [ i ][ j ] 表示 A 前 i 个位置和 B 前 j 个位置所能产生的最长公共上升子序列的长度。其中强制 A [ i ] == B [ j ],也就是最后这个位置是匹配的。若是 A [ i ] != B [ j ] 则对应函数值为0。
我们从1到n枚举i计算dp值,在枚举 i 的过程中维护
f [ k ] = max { dp [1… ( i-1 ) ][ k ] }
然后 dp [ i ][ j ] = max { f [ k ] | k < j && B [ k ] < A [ i ] },如果我们再从小到大枚举 j 的话只要边枚举 j 边记录满足条件的 f [ k ] 最大值即可。
总复杂度 O( n*m );
看看代码:


和LCIS完全一样的解法啊。
设 f [ i ][ j ][ 0/1 ] 表示第一个序列前i和第二个序列前 j 个位置,最后一个位置是上升还是下降,转移和之前一样,记录一个辅助数组即可。
注意这里是记方案数。
dp 与容斥初步
最基本的容斥模型:
给定一些条件,问全部满足的对象的个数。
答案 = 所有对象 - 至少不满足其中一个的 + 至少不满足其中两个的 - 至少不满足其中三个的 +……
证明:考虑对于一个恰好不满足k个的的对象,被计算了几次。
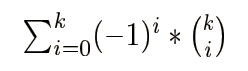
显然只有当k=0时,这个对象才会被算进答案,所以我们就证明了上面这个容斥方法的正确性。

Dp是处理计数问题应该非常常用的方法,而计数问题又常常与容斥原理相结合。
考虑 t=1 的情况,我们只需要把总的路径条数减去经过那个障碍点的路径条数就可以了。走法 = ” 左下角到障碍点的走法 ” * ” 障碍点到右上角的做法 ”;
t=2 时,设两个障碍点为 A,B,” 总的路径条数 ” - “ 经过A的路径条数 ” - “ 经过B的路径条数 ” 算出来的答案可能偏小,如果 A,B 可以同时经过,那么最终答案要加上 ” 同时经过 A,B 的路径条数 ”。
那么这道题就可以用容斥来做。随意填 - 至少遇到一个障碍的方案数 + 至少遇到两个障碍的方案数 - 至少遇见三个障碍的方案数………………
给障碍点从左到右从下到上排个序,记 f [ i ][ j ] 表示走到了第 i 个障碍点且包括第 i 个点在内强制经过了 j 个障碍点的路径条数(除此之外也可能有经过的),枚举上一个经过的障碍点即可。
转移的时候乘上一个组合数表示从 k 到 i 的走法数目:
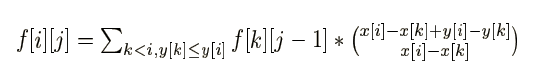
另一种容斥方法:
另一种形式的容斥dp,枚举第一个遇到的障碍是哪一个来容斥。
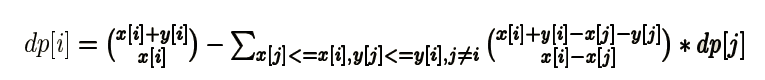
实际上这是由下面这个推出来的。

记忆化搜索
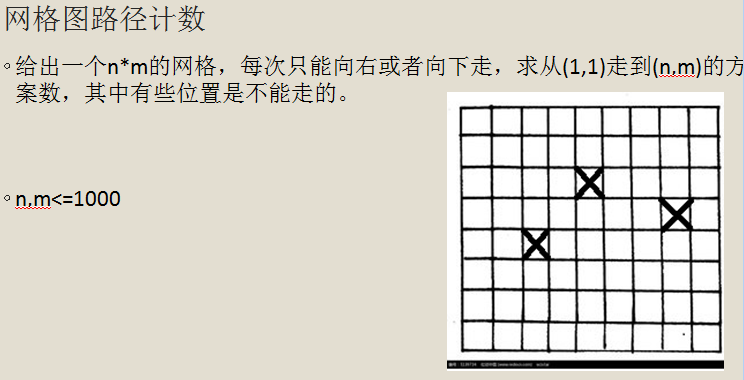
我们从另一个角度来思考这个问题。
我们用搜索算法来计算答案,先看看没有障碍的情况,有障碍只改一点。
我们发现在这个 dfs 的过程中,dfs 出来的值只与带入参数,也就是 ( x,y ) 有关,而不同的 ( x,y ) 有 N * M 个,而我们之前搜索的问题在于有大量的重复计算,多次调用同一个 ( x,y ),每次都从新计算。
有一个很直观的想法就是,第一次调用的时候就把答案记下来,之后调用不重新算,直接返回之前已经计算出的答案即可。——这就是记忆化搜索。
这是有障碍的情况,mp [ x ][ y ] == -1 表示有障碍:
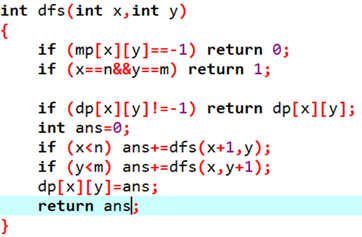

dp [ x ][ y ] 存储在当前位置下山的最大长度,它等于它旁边的(上下左右)比它矮的山的 dp 值加 1 的最大值,即 dp [ x ][ y ] = max ( dp [ x-1 ][ y ] , dp [ x ][ y-1 ] , dp[ x ][ y+1 ] , dp [ x+1 ][ y ] ) +1。
要保证对应的高度小于H [ x ][ y ] 才能取 max。
1:一般递推式动态规划还要注意枚举状态的顺序,要保证算当前状态时子状态都已经算完了。
2:但是记忆化搜索不需要,因为记忆化搜索就是个搜索,只不过把重复的部分记下来了而已。我们不用像递推一样过于关注顺序,像搜索一样直接要求什么,调用什么就好。
代码实现:
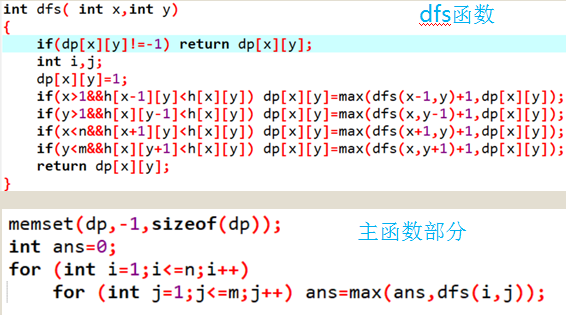

思路:手玩数据,找出最优子结构,做 dp。关键是找出划分状态的方式。
考虑分割成两个矩形,对于任意一种分割方案都一定存在一条贯穿横向或者纵向的线,那么枚举这条线即可。
然后设 f [ x ][ y ][ t ] 表示长为 x 宽为 y,面向大海的边状态是 t,最小的不满意度。转移就枚举从那个地方断开即可。
主程序如下:


红色是面向大海的部分。
记忆化搜索部分并不难,主要是分情况套论别漏下什么就好。
记忆化搜索小结
在有一些dp问题中,状态之间的转移顺序不是那么确定,并不能像一些简单问题一样写几个 for 循环就解决了。
我们可以直接计算最终要求的状态,然后在求这个状态的过程中,要调用哪个子状态就直接调用即可,但是每一个状态调用一遍之后就存下来答案,下次计算的时候就直接取答案即可,就不需要从新再计算一遍。
虽然看上去每一次都计算不少,但是因为每一个状态都计算一次,所以均摊下来,复杂度还是状态数 * 状态转移。
拓扑图 dp
拓扑图 dp 通常是在拓扑图上求关于所有路径的某种信息之和。当然这里的 “ 和 ” 的运算法则可以是加法或是取 max 和 min。或者其他定义的运算。
按拓扑序沿着有向边转移就可以了。

拓扑图dp经典题
设 f [ u ] 为以节点 u 为终点的食物链数量。
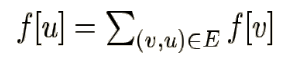
按照拓扑序的顺序转移即可。

其实我们对于一般非有关期望和概率的 dp,如果题目中每一个转移关系是双边的,那么如果我们把 dp 的每一个状态记为一个点, dp 状态之间关系构成的图就是一个拓扑图。
拓扑图 dp 实际上就是已经给了我们这个拓扑关系了,也就不需要我们自己找了,其实是更简单。

( u , v , len , cnt ) 其实就是 ( u , v ) 点对有 cnt 条长度 len 为边,求 S 到 T 的最短路径方案数。
如果 dis [ u ] + len = dis [ v ] ,说明这条边在最短路径上;
求以最短路径为前提的一些问题,果断先建最短路图。
毕竟,最短路图建出来是一个 DAG,而 DAG 就比随意的图具有更好的性质,不求白不求。
然后就是求DAG上从S到T,路径的方案数。
设 f [ u ] 为从 u 到 T 路径的方案数:
![]()
答案就是 f [ S ] 。
记忆化搜索代码实现:
拓扑排序的写法上一题中讲过了,我们这次来介绍记忆化搜索的实现方法:
初始直接调用 dfs ( S ) 即可。


枚举上式中的 s,考虑该 s 对每个 v 的贡献。
还是先求出以 s 为起点的最短路径 DAG,可以用 DAG dp 对每个 t 求出 f ( s , t ) 。
f ( s , t , v ) = f ( s , v ) * DAG 上 v 到 t 的每条路径的宽度之和。
记后者为 g ( v , t ) ,则 F ( v ) += As f ( s , v ) ∑ g ( v , t ) * At / f ( s , t ) 。
F(v)+= Asf(s,v) ∑ g(v,t)*At/f(s,t)
At / f ( s , t ) 可以看做每个 t 自带的权值。
设 G [ u ] 表示以 u 为起点的所有路径的宽度与其终点权值乘积之和。
G [ u ] = ∑ w ( u , v ) * ( G [ v ] + Av / f ( s , v ) ) | ( u , v ) ∈ DAG;
F ( v ) += As f ( s , v ) G [ v ]
按拓扑序倒序 dp 即可,记忆化也行。
基础DP练习题

枚举上下边界,然后只需要确定左右边界,就是个一维的问题,实际上就是求最大连续子段和。
当我们枚举上下边界后,你们子矩阵竖着的边也就确定了,设竖着的边的长度为 x;
那么我们可以先预处理,所有在上下界内,竖着的边为 x,横着的边为 1 的小竖型矩阵的元素和,然后跑一边最大子段和就好了。
F [ i ] = max ( 0 , f [ i-1 ] ) + val [ i ] ;
val [ i ] 表示枚举的上下界范围内第 i 列的和。