原题链接 https://www.luogu.org/problemnew/show/P1383


作为考试的T1,我的内心也是很绝望的,最难的题是T1?
首先前50分还是很好拿的,考场上许多人都水到了这50分,做法就是简单的数组模拟:
#include<iostream> #include<cstdio> #include<queue> using namespace std; int n,tail,x; //tail是有几步添加操作 char p,m,wz[100001]; int main() { //freopen("type.in","r",stdin); //freopen("type.out","w",stdout); scanf("%d",&n); for(int i=1;i<=n;i++) { cin>>p; if(p=='T') cin>>m,wz[++tail]=m; //添加 else scanf("%d",&x); if(p=='U') tail-x>=0?tail-=x:tail=0; //删除后x个元素,注意栈内元素不足x的情况 if(p=='Q') printf("%c ",wz[x]); } return 0; }
考虑100分的做法:
我们用栈将每一步操作都存下来,下面以样例为例:
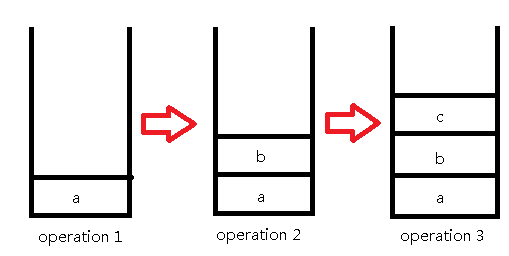
接下来的操作是询问操作,我们直接找到第x个元素输出就可以了:
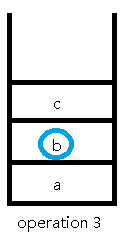
下面一步是撤销操作,撤销了两步,所以我们直接从当前第3步操作往前找两步到第1步操作来作为我们的第4步操作:
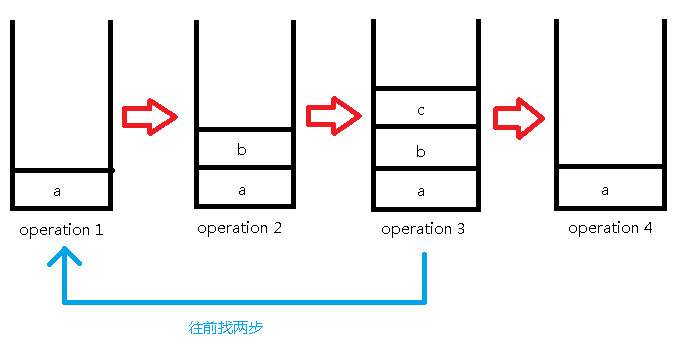
继续插入'c':
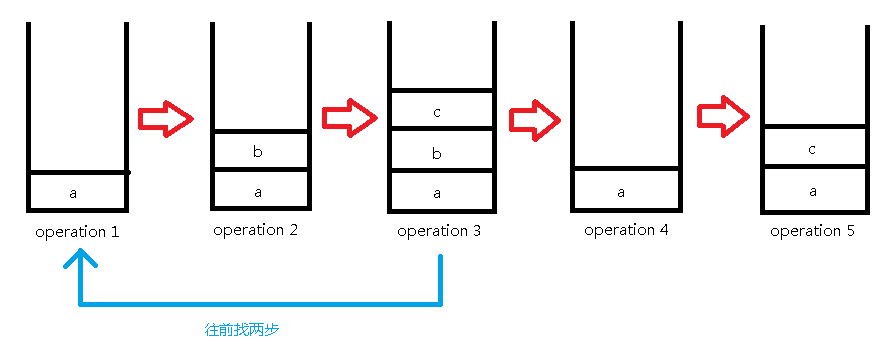
然后查询第二个元素:
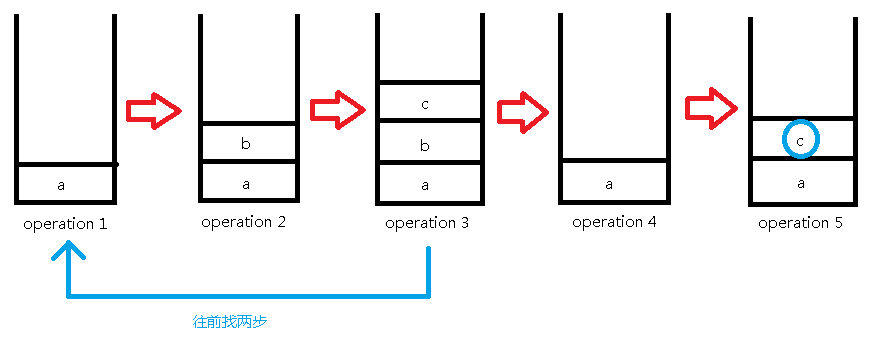
这样我们就实现了撤销功能,但是每一步操作都要拷贝前一种情况,占内存太大,显然MLE。
想想为什么空间内存会炸?你每次操作都将原数列拷贝一份再进行操作,这样一来其实有很多空间是被考来考去而不被利用的,造成了极大的空间浪费!
所以我们可以考虑用链式前向星来维护栈,它的思想是每插入一个元素我们就开辟一个新的结点指向上一个,这样我们每一步的操作不用再将之前的元素拷贝过来了,节省了很大的空间
!
首先我们用top表示一个空栈,插入一个元素 'a':
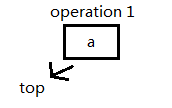
插入一个元素 'b':
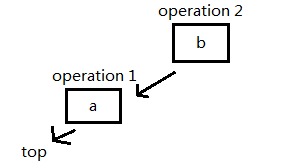
插入一个元素 'c':
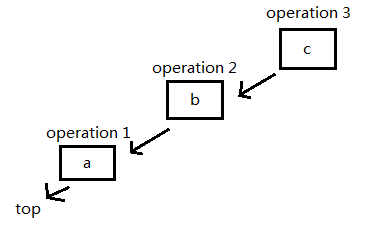
询问第二个元素,在链表里从前往后找到第二个元素:
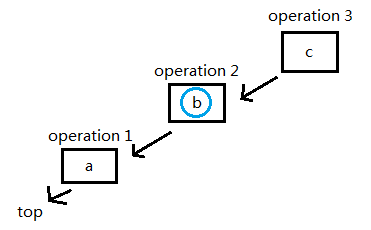
撤销两步操作,从最后一个元素往前找两步,创建新节点记录:
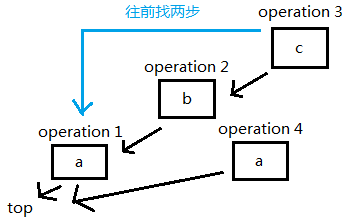
插入一个元素 'c':
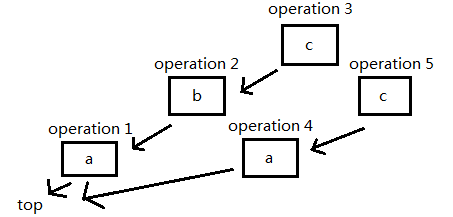
询问第二个元素,从前往后找到第二个元素:
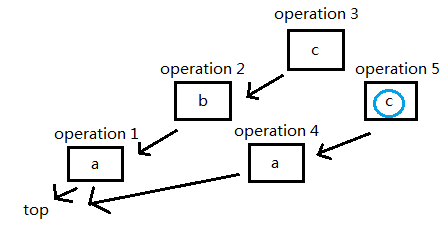
考虑到插入和撤销操作都是O(1)完成,但是查询的时候我们要先在所以的链中找出当前那一条链,如果撤销操作多了时间也是会爆炸的!还要考虑一个更为稳定的算法。
分块大法好!!!
继承上面的思路,我们改进用分块。
浅谈分块
所谓分块,顾名思义就是分成好几块。我们在用链式前向星存的时候,不再是每个结点只存一个元素了,我们每个结点存一个数组!

这样有什么好处呢?我们可以O(N / B)找到某个元素在哪!(N表示这个元素在栈里是第N个元素,每个块的大小是B)
每个块的数组大小是由我们设定的,所以当我们访问的时候可以通过 N / B 来求出前面有多少个块,然后剩下的就在一个块里了,利用数组查询的原理直接O(1)查询;
所以我们在用链表存的时候稍加一些修改就好啦:
首先我们先开一个结构体:
struct node { char *s; int now, pc; //now是当前块里有多少个元素,pc是当前块前面有多少个块 node *pre; //当前块的前一个是第几块 node() //构造函数 { now = pc = 0; s = new char[B]; //存每个块数组的元素 pre = NULL; } void copy(node *src) //构造函数 { now = src->now; pc = src->pc; pre = src->pre; for (int i = 0; i < now; i++) { s[i] = src->s[i]; } } } * head[N];
我们在插入新元素的时候,考虑有如下两种情况:
1.当前块没有满,那么我们就直接在后面开一个空位置插入就可以了;
2.若当前块满了,那么我们就新开一个块插入,注意更新 pc,* pre 的值;
void append(char x) //添加一个新元素 { if (head[lst]->now == B) //如果当前的块满了,开辟一个新块 { head[++lst] = new node; //开一个结构体类型的空间 head[lst]->pre = head[lst - 1]; //lst的前一个块是lst-1 head[lst]->pc = head[lst - 1]->pc + 1; //lst前面的块数比lst-1前面的块数多1 head[lst]->s[head[lst]->now++] = x; //添加新元素 } else //如果块没满 { head[++lst] = new node; head[lst]->copy(head[lst - 1]); //拷贝一个和上个块一毛一样的块 head[lst]->s[head[lst]->now++] = x; //添加新元素 } }
询问第x个元素的时候,由于栈是后进先出的结构,而我们要从前往后找,这就有点挠人啊;
这时候分块的作用就出来了:我们可以先求出栈内的元素个数:完整块数(数组中没有空位置) * 块的数组大小 + 当前这个块中的元素个数:
int siz = head[lst]->now + head[lst]->pc * B; //看看栈里有几个元素,now+块数*每块有几个
求出有几个元素之后,我们要从前往后找x个,不就相当于从后往前找 siz - x + 1 个嘛?正好符合栈的特点。
设 y = siz - x + 1,我们先判断这个 y 是否就在当前块范围内(y <=now),如果在的话就不用再往下找了;
如果不在的话,我们先让 y 减去 now,然后我们往前找,如果过程中 y 大于 B,那么就跳过当前块到上一个块,直到 y <=B,说明该元素就在当前块里了,那么我们直接输出就好啦;
例如:
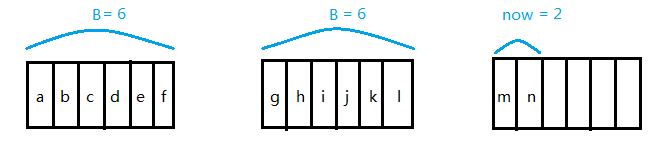
假设我们要求第3个元素,先求出所有的元素个数:2*6+2=14,那么就相当于从后往前找第 14-3+1 = 12 个元素,我们发现 12 > now,说明不在当前最后的那个块里,那么先 12 - 2 =10,意思是找完了最后一块后我们还要往前找 10 个元素;由于 10 > B,那么我们直接跳过第二块来到第一块,我们还需要找 10 - 6 = 4 个元素;发现 4 < 6,说明就在当前块里,利用数组直接输出 a [ 6 - 4 ] = a [ 2 ] = c,注意这里我们还是要再转换成从前往后找的。
撤销操作是最简单的,我们先设 lat 为当前这是第 lat 步操作,如果我们撤销了 x 步操作,那么直接让第 lst + 1 步操作的指针指向第 lst - x 步操作就OK了;
完整指针版本的AC代码:
#include <cmath> #include <cstdio> #include <cstring> template <class T> inline void read(T &num) { bool flag = 0; num = 0; char c = getchar(); while ((c < '0' || c > '9') && c != '-') c = getchar(); if (c == '-') { flag = 1; c = getchar(); } num = c - '0'; c = getchar(); while (c >= '0' && c <= '9') num = (num << 3) + (num << 1) + c - '0', c = getchar(); if (flag) num *= -1; } inline void read(char &c) { do { c = getchar(); } while (c == ' ' || c == ' ' || c == ' '); } template <class T> inline void output(T num) { if (num < 0) { putchar('-'); num = -num; } if (num >= 10) output(num / 10); putchar(num % 10 + '0'); } template <class T> inline void outln(T num) { output(num); putchar(' '); } template <class T> inline void outps(T num) { output(num); putchar(' '); } template <class T> inline T max(T a, T b) { return a < b ? b : a; } const int N = 100000; int n, B; struct node { char *s; int now, pc; //now是当前块里有多少个元素,pc是当前块前面有多少个块 node *pre; //当前块的前一个是第几块 node() //构造函数 { now = pc = 0; s = new char[B]; //存每个块数组的元素 pre = NULL; } void copy(node *src) //构造函数 { now = src->now; pc = src->pc; pre = src->pre; for (int i = 0; i < now; i++) { s[i] = src->s[i]; } } } * head[N]; //一个指针数组 int lst; //当前这是第几步操作 void append(char x) //添加一个新元素 { if (head[lst]->now == B) //如果当前的块满了,开辟一个新块 { head[++lst] = new node; //开一个结构体类型的空间 head[lst]->pre = head[lst - 1]; //lst的前一个块是lst-1 head[lst]->pc = head[lst - 1]->pc + 1; //lst前面的块数比lst-1前面的块数多1 head[lst]->s[head[lst]->now++] = x; //添加新元素 } else //如果块没满 { head[++lst] = new node; head[lst]->copy(head[lst - 1]); //拷贝一个和上个块一毛一样的块 head[lst]->s[head[lst]->now++] = x; //添加新元素 } } char query(int x) //查询操作 { int siz = head[lst]->now + head[lst]->pc * B; //看看栈里有几个元素,now+块数*每块有几个 x = siz - x + 1; //从前往后找x个,相当于从后往前找siz-x+1个 if (x <= head[lst]->now) //如果在当前块里,直接输出就好了 { return head[lst]->s[head[lst]->now - x]; } x -= head[lst]->now; //减去当前块元素的个数,继续往前找 node *now = head[lst]->pre; //移到当前块的前一个块 while (x > B) //如果一直大于每个块的最大块数,也就是说可以跳块,那就往前跳 { now = now->pre; //跳到前一个 x -= B; } return now->s[B - x]; //跳完之后一定在当前块里,直接输出,因为我们是从后往前找,所以正确答案是B-x } int main() { read(n); B = sqrt(n); head[0] = new node; for (int i = 1; i <= n; i++) { char op; read(op); if (op == 'T') //添加一个元素 { char x; read(x); append(x); } if (op == 'U') //撤销操作 { int x; read(x); head[lst + 1] = head[lst - x]; //撤销x步,直接将第lst+1步的指针指向lst往前x步就好了 lst += 1; } if (op == 'Q') //查询操作 { int x; read(x); putchar(query(x)); //查询栈里的第x个元素 putchar(' '); } } }