



大眼一看最下面的题意解释的话,发现这和洛谷P1310表达式的值挺像的,大概都是给定一些运算符号,让最后的表达式为true的概率,为false的概率啥的QwQ~;
然后这个题嘛?就是在所有的运算符中提溜出一个作为最后一次运算的运算符,然后我们去算这个运算符左边的那一堆式子,然后再算右边那一堆式子,最后再算一下最后一个运算符对应的运算就好啦!
那么怎么算这个运算符左边的式子和右边的式子呢?我们再从左边的式子中找出一个运算符最为最后一次运算的运算符,然后算它左边的式子,算它右边的式子……
我们发现这就是一个枚举 + 递归的过程是吧QwQ~
直到我们一直递归到式子长度为1的情况了,这时候如果是' t '那就对应一种表达式为true的情况,如果是' f '那就对应了一种表达式为false的情况;
我们开两个数组 t [ i ][ j ]表示区间 [ i,j ]的表达式为true的方案数,f [ i ][ j ]表示区间 [ i,j ]的表达式为false的方案数,那么有如下边界设置:
for(int i=1;i<=n;i++) { if(s[i]=='t') //贡献了一个为true的方案 { t[i][i]=1,f[i][i]=0; } else //否则就贡献一个为false的方案 { f[i][i]=1,t[i][i]=0; } } //s数组里存的是't' or 'f'
那么最终的答案就是:
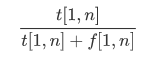
for(int len=2;len<=n;len++) //枚举区间长度 for(int i=1;i+len-1<=n;i++) //枚举区间左端点的位置 { int j=i+len-1; //计算出区间右端点的位置 for(int k=i;k<j;k++) //枚举区间内的中间点 …………… }
已经确定了要使用区间DP了,接下来的任务就是要找状态转移方程了(下面的过程就和分析P1310表达式的值 的时候几乎一样了);
题目中只有三种运算符:
与&,或 |,异或 ^,先了解一下它们的运算规则:
&:要使 x&y=1,x和y必须都为1;要使 x&y=0,x和y有一个为0;
| :要使x | y=1,x和y有一个为1;要使x | y=0,x和y必须都为0;
^:要使x ^ y=1,x和y必须不相同(即x=0,y=1或 x=1,y=0);要使x ^ y=0,x和y必须相同(即x=0,y=0或 x=1,y=1);
然后我们就可以根据它们的运算法则来确定状态转移方程啦(还运用了乘法计数原理):
for(int len=2;len<=n;len++) //枚举区间长度 { for(int i=1;i+len-1<=n;i++) //枚举区间左端点的位置 { int j=i+len-1; //计算出区间右端点的位置 for(int k=i;k<j;k++) //枚举区间内的中间点的运算符号 { if(ops[k]=='&') //&运算 { t[i][j]=(t[i][j]+(t[i][k]*t[k+1][j])%mod)%mod; //必须两个都为true f[i][j]=(f[i][j]+(t[i][k]*f[k+1][j])%mod+(f[i][k]*t[k+1][j])%mod+(f[i][k]*f[k+1][j])%mod)%mod; //只需要其中一个为false } if(ops[k]=='|') //|运算 { t[i][j]=(t[i][j]+(t[i][k]*f[k+1][j])%mod+(f[i][k]*t[k+1][j])%mod+(t[i][k]*t[k+1][j])%mod)%mod; //只需要其中一个为true f[i][j]=(f[i][j]+(f[i][k]*f[k+1][j])%mod)%mod; //必须两个都为false } if(ops[k]=='^') //异或运算 { t[i][j]=(t[i][j]+(t[i][k]*f[k+1][j])%mod+(f[i][k]*t[k+1][j])%mod)%mod; //必须两个不同 f[i][j]=(f[i][j]+(f[i][k]*f[k+1][j])%mod+(t[i][k]*t[k+1][j])%mod)%mod; //必须两个相同 } } } }
注意到我们的答案是需要取模的,而最后的答案还涉及到了除法,所以最后我们还需要一步求乘法逆元的过程!
#include<bits/stdc++.h> using namespace std; inline int read() { int X=0,w=1; char c=getchar(); while(c<'0'||c>'9') { if (c=='-') { w=-1; } c=getchar(); } while(c>='0'&&c<='9') { X=(X<<3)+(X<<1)+c-'0'; c=getchar(); } return X*w; } inline char gc() { char c; do { c=getchar(); } while(c==' '||c==' '||c==' '||c=='�'||c==' '); } int n; long long x,y; char s[501],ops[501]; long long t[501][501],f[501][501]; const int mod=998244353; void exgcd(long long a,long long b,long long &x,long long &y) //扩展欧几里得求逆元 { if(b==0) { x=1;y=0;return ; } exgcd(b,a%b,x,y); long long r=x; x=y; y=r-(a/b)*x; } int main() { n=read(); for(int i=1;i<=n-1;i++) { s[i]=gc(); //存't' or 'f' ops[i]=gc(); //存运算符 } //这么读入的原因是注意到't','f'是和运算符一个一个隔开的 s[n]=gc(); for(int i=1;i<=n;i++) { if(s[i]=='t') //边界条件 { t[i][i]=1,f[i][i]=0; } else { f[i][i]=1,t[i][i]=0; } } for(int len=2;len<=n;len++) //枚举区间长度 { for(int i=1;i+len-1<=n;i++) //枚举区间左端点的位置 { int j=i+len-1; //计算出区间右端点的位置 for(int k=i;k<j;k++) //枚举区间内的中间点 { if(ops[k]=='&') //&运算 { t[i][j]=(t[i][j]+(t[i][k]*t[k+1][j])%mod)%mod; //必须两个都为true f[i][j]=(f[i][j]+(t[i][k]*f[k+1][j])%mod+(f[i][k]*t[k+1][j])%mod+(f[i][k]*f[k+1][j])%mod)%mod; //只需要其中一个为false } if(ops[k]=='|') //|运算 { t[i][j]=(t[i][j]+(t[i][k]*f[k+1][j])%mod+(f[i][k]*t[k+1][j])%mod+(t[i][k]*t[k+1][j])%mod)%mod; //只需要其中一个为true f[i][j]=(f[i][j]+(f[i][k]*f[k+1][j])%mod)%mod; //必须两个都为false } if(ops[k]=='^') //异或运算 { t[i][j]=(t[i][j]+(t[i][k]*f[k+1][j])%mod+(f[i][k]*t[k+1][j])%mod)%mod; //必须两个不同 f[i][j]=(f[i][j]+(f[i][k]*f[k+1][j])%mod+(t[i][k]*t[k+1][j])%mod)%mod; //必须两个相同 } } } } exgcd(t[1][n]+f[1][n],mod,x,y); cout<<t[1][n]*((x+mod)%mod)%mod; return 0; }