一. 基本实现
a .首先选择一个顶点作为起始结点,并将其染成灰色,其余结点为白色。
b. 将起始结点放入队列中。 并找出所有与之邻接的结点。
c. 从队列首部选出一个顶点,将找到的邻接结点放入队列尾部,
将已访问过结点涂成黑色。如果顶点的颜色是灰色,表示已经放入了队列,
如果顶点的颜色是白色,表示还没有发现 d. 按照同样的方法处理队列中的下一个结点。
基本就是出队的顶点变成黑色,在队列里的是灰色,还没入队的是白色。
例如,从顶点1开始进行广度优先搜索:
初始状态,从顶点1开始,队列={1}
访问1的邻接顶点,1出队变黑,2,3入队,队列={2,3,}
访问2的邻接结点,2出队,4入队,队列={3,4}
访问3的邻接结点,3出队,队列={4}
访问4的邻接结点,4出队,队列={ 空} 结点5对于1来说不可达。
二. 双端队列
普通队列用于边权为定值的最短路搜索。
且每次到达都是最优的决策(不用取min)。
因为所有状态按照 入队的先后顺序 具有 层次单调性,每次扩展,都往外走一步,
满足从起始到该状态的最优性(不用取min/也不用比大小,如果如此失去了意义)。
双端队列可以进行边权为1/0的最短路搜索。
对于一条边 u 到 v ,如果此边权值为0,我们将它 push_front(v) ,否则 push_back(k),
每次取队首,这样我们保证了单调性(即每次优先选择最优的)。
注意细节:把某一方格对角两点的连线看成边,若和原状态匹配边权为0,否则为1。
我们放入队列里的还有u,这样才能做到将每次取出的时候更新,
也就是说在队列中放入二元组(u,v)。复杂度:O(r*c)。
三. Hash判重
1、哈希表的特征
深搜中的【路径寻找问题】,常常可以用构造Hash表实现。
Hash是根据关键码值(Key value)而直接进行访问的数据结构。
它通过把关键码值映射到表中一个位置来访问记录,以加快查找的速度。
这个映射函数叫做散列函数,存放记录的数组叫做散列表。
这里的对应关系 f 称为散列函数,又称为哈希(Hash函数),
散列将记录存储在一块连续的存储空间中,这块连续存储空间称为散列表或哈希表。
哈希表是把Key通过一个固定的算法函数,即所谓的哈希函数转换成一个整型数字,
然后就将该数字对数组长度进行取余,取余结果就当作数组的下标,
将value存储在以该数字为下标的数组空间里。
(或:把任意长度的输入(又叫做预映射),通过散列算法,变换成固定长度的输出,
该输出就是散列值。这种转换是一种压缩映射,也就是,散列值的空间通常远小于输入的空间,
不同的输入可能会散列成相同的输出,而不可能从散列值来唯一的确定输入值。
简单的说就是一种将任意长度的消息压缩到某一固定长度的消息摘要的函数。)
而当使用哈希表进行查询的时候,就是再次使用哈希函数将key转换为对应的数组下标,
并定位到该空间获取value,如此一来,就可以充分利用到数组的定位性能进行数据定位。
2、哈希表的实现方法:拉链法
数组的特点是:寻址容易,插入和删除困难。
而链表的特点是:寻址困难,插入和删除容易。
一种寻址容易,且插入删除容易的数据结构:哈希表。
哈希表最常用的实现方法——拉链法,我们可以理解为“链表的数组”,如图:
左边很明显是数组,数组的每个成员包括一个指针,指向一个链表的头,
根据元素的一些特征把元素分配到不同的链表中去,再根据这些特征,找到正确的链表和元素。
3、Hash的应用
1、Hash主要用于信息安全领域中加密算法,它把一些不同长度的信息转化为128位编码,
这些编码值叫做Hash值。Hash即找到一种数据内容和数据存放地址之间的映射关系。
2、查找:哈希表,又称为散列,是一种更加快捷的查找技术。
我们之前的查找思路:集合中拿出来一个元素,比较,不等就缩小范围继续查找。
而哈希表是完全另外一种思路:知道key值可以直接计算出这个元素在集合中的位置。
3、Hash表在海量数据处理中有着广泛应用。
Hash Table的查询速度非常的快,几乎是O(1)的时间复杂度。
Q : 如果两个字符串在哈希表中对应的位置相同怎么办?
可以转化成链表来解决,只要在哈希表的每个入口挂一个链表,保存所有对应的字符串就OK了。
4、散列法
元素特征转变为数组下标的方法就是散列法。下面列出三种比较常用的:
1,除法散列法
最直观的一种,上图使用的就是这种散列法,公式形如: index = value % 16
2,平方散列法
求index是非常频繁的操作,而乘法的运算要比除法来得省时,
所以我们考虑把除法换成乘法和一个位移操作。公式: index = (value * value) >> 28
(右移,除以2^28。记法:左移变大,是乘。右移变小,是除。)
3,斐波那契(Fibonacci)散列法
找出一个理想的乘数,而不拿value本身当作乘数呢。
1)对于16位整数而言,这个乘数是40503
2)对于32位整数而言,这个乘数是2654435769
3)对于64位整数而言,这个乘数是11400714819323198485
这几个“理想乘数”是如何得出来的呢?这跟一个法则有关,叫黄金分割法则,
而描述黄金分割法则的最经典表达式无疑就是著名的斐波那契数列,
即如此形式的序列:0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233,377, 610…。
对我们常见的32位整数而言,公式: index = (value * 2654435769) >> 28
如果用这种斐波那契散列法的话,那上面的图就变成这样了:
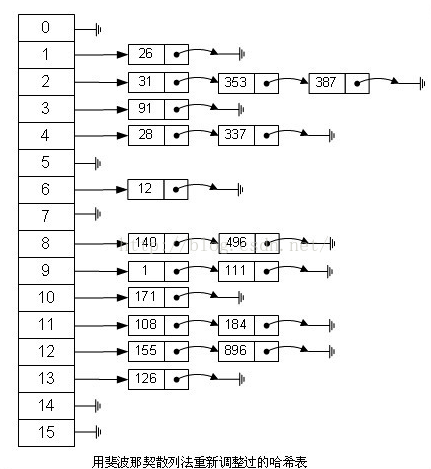
注:用斐波那契散列法调整之后会比原来的取模散列法好很多。
【Hash表的常见构造方法】
状态压缩法——用二进制记录状态。
直接取余法——选取一个质数M作为除数。
平方取中法——计算关键值的平方,取中间的r位。
折叠法——把所有字符的ASCII码加起来。