原题 传送门
【题目描述】
长 L 米,宽 W 米的草坪里装有 n 个浇灌喷头。每个喷头都装在草坪中心线上(离两边各 W2 米)。我们知道每个喷头的位置(离草坪中心线左端的距离),以及它能覆盖到的浇灌范围。
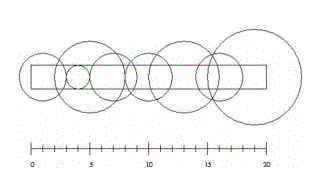
请问:如果要同时浇灌整块草坪,最少需要打开多少个喷头?
【输入】
输入包含若干组测试数据。
第一行一个整数 TT 表示数据组数;
每组数据的第一行是整数 nn、LL 和 WW;
接下来的 nn 行,每行包含两个整数,给出一个喷头的位置和浇灌半径(上面的示意图是样例输入第一组数据所描述的情况)。
【输出】
对每组测试数据输出一个数字,表示要浇灌整块草坪所需喷头数目的最小值。如果所有喷头都打开也不能浇灌整块草坪,则输出 −1−1 。
【输入样例】
3 8 20 2 5 3 4 1 1 2 7 2 10 2 13 3 16 2 19 4 3 10 1 3 5 9 3 6 1 3 10 1 5 3 1 1 9 1
【输出样例】
6 2 -1
【提示】
数据范围:
对于 100% 的数据,n≤15000。
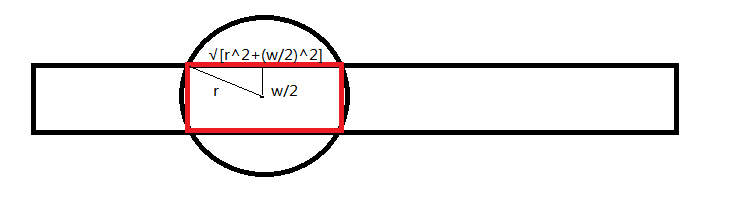
对于这个题,首先我们要考虑到装置实际覆盖的范围:
由于曲线不好处理,所以我们可以将覆盖面积近似的看成是图中红色矩形覆盖的面积(这样对结果不造成影响)
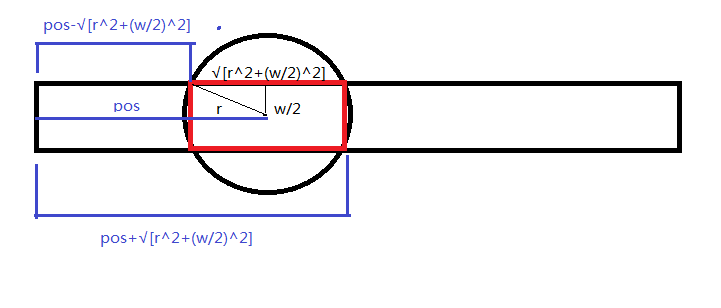
那么这个矩阵的左端点与大区间最左侧的距离为 pos-√[r^2+(w/2)^2],矩形的右端点与大区间最左侧的距离为pos+√[r^2+(w/2)^2];
接下来是贪心思路:
1.在读入每个喷水装置的数据后,我们紧接着计算出实际矩形的左端点和右端点的距离l和r,记录在结构体中;
2.根据矩形左端点从大到小排序;
3.我们设double类型的s来表示已经覆盖区间的范围,初始值为0;
4.我们先用q来暂时储存一下s每次操作前的值,然后访问每一个l<=s且在cnt内的点,找出最大的r,让s=r(此时这个r是最大的那个r);
判无解:若q==s且s<l,则说明无解(意思就是没能找到一个装置来更新s,并且s还未覆盖整个区间)
好啦,代码如下:
#include<cstdio> #include<iostream> #include<algorithm> #include<cmath> using namespace std; int read() //读入优化 { char ch=getchar(); int a=0,x=1; while(ch<'0'||ch>'9') { if(ch=='-') x=-x; ch=getchar(); } while(ch>='0'&&ch<='9') { a=(a<<3)+(a<<1)+(ch-'0'); ch=getchar(); } return a*x; } int t,n,l,w; int pos,R,ans,cnt; struct water { double l,r; //l是装置实际覆盖区间的左端点,r是右端点 }a[15001]; int cmp(water x,water y) //按照左端点从大到小排序 { return x.l<y.l; } int main() { t=read(); //t组数据 for(int i=1;i<=t;i++) { n=read(); l=read(); w=read(); cnt=0; //cnt是有用的装置的个数,条件为r>w/2 for(int j=1;j<=n;j++) { pos=read(); //装置圆心距区间最左端的距离 R=read(); if(R<=w/2) continue; cnt++; a[cnt].l=pos-sqrt(R*R-(w/2.0)*(w/2.0)); a[cnt].r=pos+sqrt(R*R-(w/2.0)*(w/2.0)); } sort(a+1,a+1+cnt,cmp); double s=0,q; //我们已经将区间覆盖了s米 int k=1,flag=0,ans=0; while(s<l) //覆盖不满就一直找喷水装置 { ans++; q=s; for(;a[k].l<=q&&k<=cnt;k++) //在s左端找到一个右端点最大的值 if(a[k].r>s) s=a[k].r; //让s更新为最大的r if(s==q&&s<l) {flag=1;cout<<0<<endl;break;} //判断无解 } if(flag==0) cout<<ans<<endl; } return 0; }
在此对贪心做一下小结:
贪心算法是指:
在每一步求解的步骤中,它要求“贪婪”的选择最佳操作,并希望通过一系列的最优选择,能够产生一个问题的(全局的)最优解。
贪心算法每一步必须满足一下条件:
1、可行的:即它必须满足问题的约束。
2、局部最优:他是当前步骤中所有可行选择中最佳的局部选择。
3、不可取消:即选择一旦做出,在算法的后面步骤就不可改变了。
贪婪算法并没有固定的算法解决框架,算法的关键是贪婪策略的选择,根据不同的问题选择不同的策略。必须注意的是策略的选择必须具备无后效性,即某个状态的选择不会影响到之前的状态,只与当前状态有关,所以对采用的贪婪的策略一定要仔细分析其是否满足无后效性。