众所周知,高斯消元可以用来求 $n$ 元一次方程组的,主要思想就是把一个 $n*(n+1)$ 的矩阵的对角线消成 $1$,除了第 $n+1$ 列(用来存放 $b$ 的)的其他全部元素消成 $0$,是不是听起来有点不可思议??!
$NO NO NO!$
这不就是初中学的代入消元和加减消元嘛,思路一样的。
$Step 1:$将所给出的 $n$ 元一次方程组的每个未知数系数和等号后面的常数写成一个 $n*(n+1)$ 的矩阵
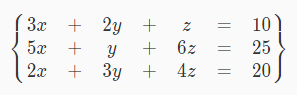
比如这个三元一次方程组我们就可以写成如下 $3×4$ 的矩阵:

$Step 2 :$运用矩阵的各种性质,来将矩阵消成对角线上的元素为 $1$,并且除了第 $n+1$ 列其余元素均为 $0$ 的矩阵,
这样我们就很容易的得出每个未知数的值:分别是从上到下第 $n+1$ 列的值(因为这时候每个未知数的系数都为 $1$)
那么是神马神奇性质呐???找度娘啊
(1) 任意交换矩阵的两行或两列,矩阵不变;
(2)矩阵任意行或列 $a_i$ 加上或减去任意 $k$ 倍的任意行或列($a_i$ 行也可以加减 $k$ 倍的 $a_i$ 行),矩阵不变;
………………………………
其余的性质这里就用不到啦,这两条性质足矣。
好啦,下面说一下怎么个消法(重点 嘤嘤嘤~)

以上面的矩阵为例:

明确我们的目的:把矩阵消成对角线为 $1$,除了第 $n+1$ 列其余元素都为 $0$。
也就是说,每一列都至少有一个元素不为 $0$,若有一列全为 $0$ 肯定有第 $i$ 行第 $i$ 列消不成 $1$,此时无解
不理解的话也可以从方程组的数学角度来思考一下:
我们把每个未知数的系数写成矩阵,所以矩阵的某一列就是某一未知数的全部系数,
如果全为 $0$,那么不就是没有这个未知数吗?那么这个未知数的值就不能确定了,那不就是无解吗?
知道了这个,我们就可以对这个矩阵进行初步判定:
for(int i=1;i<=n;i++) { pl=i; //从第i行开始往下找,一直找到一个第i列不为0的行 while(a[pl][i]==0&&pl<=n) pl++; // 判断第i列元素非0的最上行,因为第i行第i列元素不能为0 if(pl==n+1) {cout<<"No Solution";return 0;} //一直判到了n+1行,可是一共才只有n行,说明有一列全为0,无解 for(int j=1;j<=n+1;j++) //将第i行元素与第pl行第i列不为0的那一行与当前行交换 swap(a[i][j],a[pl][j]); //保证第i行第i列不为0 }
这样一来,我们就保证了第 $i$ 行第 $i$ 列的元素不为 $0$,可是我们要让第 $i$ 行第 $i$ 列的值整成 $1$ 啊,我们可以用性质 $(2)$,让第i行的每个元素都除以第 $i$ 行第 $i$ 列的值
注意:这里用到了除法,就有可能出现小数,所以我们要用 $double$ 类型定义二维数组矩阵
double k=a[i][i]; //让第i行每个元素都除以a[i][i]使得a[i][i]为1 for(int j=1;j<=n+1;j++) a[i][j]=a[i][j]/k; //将第i行第i列的元素消成1,注意同行进行同样的操作
我们就让第 $i$ 行第 $i$ 列的元素搞成 $1$ 列,继续完成接下来的任务:顺便把第 $i$ 列的其他元素搞成 $0$;
我们已经把第 $i$ 行的搞成了$1$,所以我们只要把其余行的每个元素都减去本行的首元素*第 $i$ 行的对应元素(为什么是第 $i$ 行呢?仗着第 $i$ 行第 $i$ 列的元素是 $1$ 比较好消)
for(int j=1;j<=n;j++) { if(i!=j) //将第i列除了第i行的元素全消成0 { //方法是第j行每个元素a[j][m]都减去a[j][1]*a[i][m] double ki=a[j][i]; for(int m=1;m<=n+1;m++) a[j][m]=a[j][m]-ki*a[i][m]; } }
到这里就 $OK$ 啦,最后输出第 $n+1$ 列的元素就是每个未知数的解啦!
完整代码如下:
#include<iostream> #include<cstdio> #include<cmath> using namespace std; int n,pl; double a[1001][1001]; int main() { cin>>n; for(int i=1;i<=n;i++) for(int j=1;j<=n+1;j++) cin>>a[i][j]; for(int i=1;i<=n;i++) { pl=i; while(a[pl][i]==0&&pl<=n) pl++; // 判断第i列首元素非0的最上行,因为第i行第i列元素不能为0 if(pl==n+1) {cout<<"No Solution";return 0;} //一直判到了n+1行,可是一共才只有n行,说明有一列全为0,无解 for(int j=1;j<=n+1;j++) //将第i行第i列元素不为0的那一行与当前行交换 swap(a[i][j],a[pl][j]); double k=a[i][i]; //让第i行每个元素都除以a[i][i]使得a[i][i]为1 for(int j=1;j<=n+1;j++) a[i][j]=a[i][j]/k; //将第i行第i列的元素消成1,注意同行进行同样的操作 for(int j=1;j<=n;j++) { if(i!=j) //将第i列除了第i行的元素全消成0 { //方法是第j行每个元素a[j][m]都减去a[j][1]*a[i][m] double ki=a[j][i]; for(int m=1;m<=n+1;m++) a[j][m]=a[j][m]-ki*a[i][m]; } } } for(int i=1;i<=n;i++) printf("%.2lf ",a[i][n+1]); return 0; }
大家一定跃跃欲试了吧,给大家推荐一个洛谷板子题,巩固一下吧。