今天是李昊老师的讲授~~
总结了一下今天的内容：
1.高精度算法
（1） 高精度加法
思路：模拟竖式运算
注意：进位
优化：压位
程序代码：
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<cstdlib>
using namespace std;
char a1[1000],b1[1000];
int a[1000],b[1000],c[1000];
int main(){
scanf("%s",a1);
scanf("%s",b1);
int lena=strlen(a1);
for(int i=lena-1;i>=0;i--)a[lena-i]=a1[i]-'0';
int lenb=strlen(b1);
for(int i=lenb-1;i>=0;i--)b[lenb-i]=b1[i]-'0';
int lenc=max(lena,lenb);
for(int i=1;i<=lenc;i++)c[i]=a[i]+b[i]; //先将每一对应位加起来
for(int i=1;i<=lenc;i++){
c[i+1]+=c[i]/10; //进位
c[i]%=10;
}
while(c[lenc+1]>0) lenc+=1; //如果位数增多，则lenc++
for(int i=lenc;i>0;i--)
cout<<c[i];
return 0;
}
考虑负数的情况：
若只有一个负数，那么就成为正加数-另一个加数的形式；
若有两个负数，那么先算两个数的绝对值的和，再加上个负号‘-’；
（2） 高精度减法
思路：模拟竖式运算，考虑进位
注意：结果为0的情况
程序代码：
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<cstdlib>
using namespace std;
char a1[1000],b1[1000];
int a[1000],b[1000],c[1000];
int main(){
scanf("%s",a1);
scanf("%s",b1);
int lena=strlen(a1);
for(int i=lena-1;i>=0;i--)a[lena-i]=a1[i]-'0';
int lenb=strlen(b1);
for(int i=lenb-1;i>=0;i--)b[lenb-i]=b1[i]-'0';
int lenc=max(lena,lenb);
for(int i=1;i<=lenc;i++)c[i]=a[i]-b[i]; //先将每一对应位都相减，方便借位处理
for(int i=1;i<=lenc;i++){
if(c[i]<0) //若不够0，就向高位借位+10，高位--
{
c[i]+=10;
c[i+1]--;
}
}
while(c[lenc]==0) lenc--; //除去前导0
for(int i=lenc;i>0;i--)
cout<<c[i];
return 0;
}
考虑负数的情况：
若只有一个负数：
<1>负数-正数 转化为两数绝对值相加，然后在前面加个负号‘-’；
<2>正数-负数 转化为两数绝对值相加；
若有两个负数：
转化为被减数的绝对值-减数的绝对值；
！！！小数减大数de处理方法：
用大数减小数，然后在前面加上负号‘-’；
（3） 高精度乘法
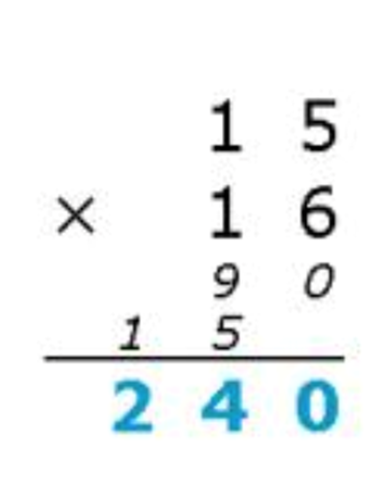
思路：模拟竖式运算，考虑进位
注意：结果为0的情况
程序代码：
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<cstdlib>
using namespace std;
char a1[1000],b1[1000];
int a[1000],b[1000],c[1000];
int main(){
scanf("%s",a1);
scanf("%s",b1);
int lena=strlen(a1);
for(int i=lena-1;i>=0;i--)a[lena-i]=a1[i]-'0';
int lenb=strlen(b1);
for(int i=lenb-1;i>=0;i--)b[lenb-i]=b1[i]-'0';
int lenc;
for(int i=1;i<=lena;i++)
for(int j=1;j<=lenb;j++)
c[i+j-1]+=a[i]*b[j]; //对应位相乘
for(int i=1;i<lena+lenb;i++)
{
c[i+1]+=c[i]/10; //进位
c[i]%=10;
}
lenc=lena+lenb-1;
while(c[lenc+1]>0) lenc++; //如果位数增多，lenc++
for(int i=lenc;i>0;i--)
cout<<c[i];
return 0;
}
考虑负数的情况：
若有一个负数： 正常绝对值相乘，前面加负号‘-’；
若有两个负数： 正常绝对值相乘；
（4） 高精度除法 ——高精除单精
思路：模拟竖式运算
程序代码：
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<cstdlib>
using namespace std;
char a1[1000];
int a[1000],b[1000],c[1000],b1;
int main(){
scanf("%s",a1);
cin>>b1;
int lena=strlen(a1);
for(int i=lena-1;i>=0;i--)a[lena-i]=a1[i]-'0';
for(int i=lena;i>0;i--){
c[i]=a[i]/b1;
a[i-1]+=(a[i]%b1)*10; 第lena位除以b1后的余数*10+第lena-1位的数继续除
}
while(c[lena]==0 && lena>0)lena--;
for(int i=lena;i>0;i--)printf("%d",c[i]);
return 0;
}
2.模意义下运算
例：
在模7意义下的运算：
3*3=9≡2 （mod 7）
4+5=9≡2 （mod 7）
4-5=-1≡6 （mod 7）
注意：无除法运算
那碰到除法的怎么办呢？？？
假设a*b=t（mod p）：
我们都知道费马小定理：
如果p是一个质数，而整数a不是p的倍数，则有a^（p-1）≡1（mod p）
t*a^（p-2）≡b （mod p）
t/a≡b （mod p）
so 模意义下/a相当于*a^（p-2）
模意义下运算的性质：
1.满足基本的交换律，分配率，结合律；
2.对中间结果取模不影响最终答案；
3.快速幂
首先让我们思考一下怎么求a^b%p？
有两种求法：
分治
简单说一下，就是要求a^b，那么我们就求a^(b/2)再平方就好啦，求a^(b/2)同理
快速幂
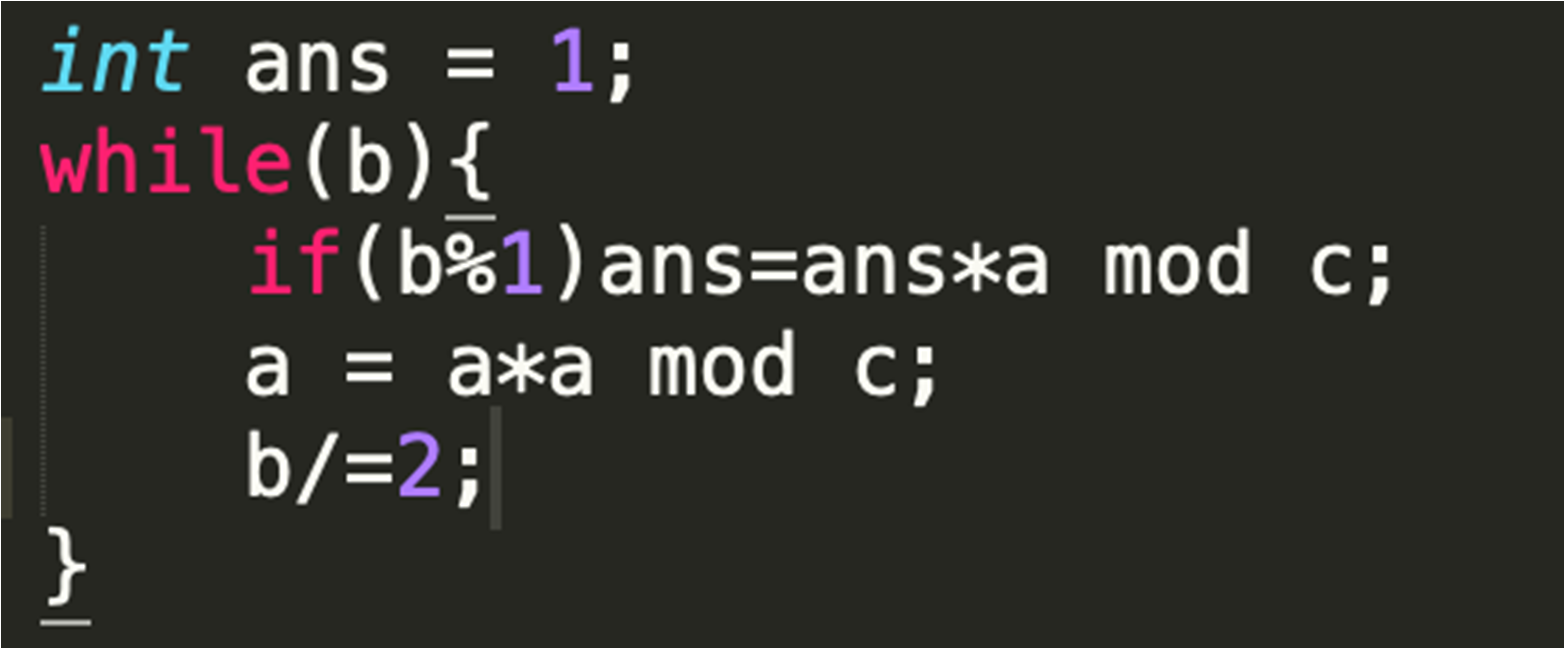
4.费马小定理
如果p是一个质数，而整数a不是p的倍数，则有a^（p-1）≡1（mod p）
应用：
计算组合数C（n，m）%（10^9+7）
C（n，m）=n!/（（n-m）！*m！）
=n!*（（n-m）！*m！）^（p-2）
=n!*（(（n-m）!)^（p-2）*(m！)^（p-2））
所以我们只要预处理任意n！，（n！）^（p-2）就好了
程序代码：
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<cstdlib>
using namespace std;
typedef long long ll;
typedef long double ld;
typedef pair<int,int> pr;
const double pi=acos(-1);
#define rep(i,a,n) for(int i=a;i<=n;i++)
#define per(i,n,a) for(int i=n;i>=a;i--)
#define Rep(i,u) for(int i=head[u];i;i=Next[i])
#define clr(a) memset(a,0,sizeof a)
#define pb push_back
#define mp make_pair
#define fi first
#define sc second
ld eps=1e-9;
ll pp=1000000007;
ll mo(ll a,ll pp){if(a>=0 && a<pp)return a;a%=pp;if(a<0)a+=pp;return a;} //模优化
ll powmod(ll a,ll b,ll pp){ll ans=1;for(;b;b>>=1,a=mo(a*a,pp))if(b&1)ans=mo(ans*a,pp);return ans;} //快速幂
ll read(){
ll ans=0;
char last=' ',ch=getchar();
while(ch<'0' || ch>'9')last=ch,ch=getchar();
while(ch>='0' && ch<='9')ans=ans*10+ch-'0',ch=getchar();
if(last=='-')ans=-ans;
return ans;
}
//head
ll b[110000],inv[110000];
int Q;
ll C(int n, int m){
if(n<m)return -1;
if(m==0 || m==n)return 1;
return b[n]*inv[n-m]%pp*inv[m]%pp; //求组合数 ，运用的组合数公式
}
int main(){
Q=read(); //看不懂的快读
pp=read();
b[0]=1;
rep(i,1,100000)b[i]=b[i-1]*i%pp; //算1~100000的阶乘
rep(i,1,100000)inv[i]=powmod(b[i],pp-2,pp); //算1！~100000！的逆元
cout<<C(5,2);
}
5.最大公约数，最小公倍数
求最大公约数可以用欧几里得算法
gcd（a，b）=gcd（b，a%b）；
这样我们就可以递归求最大公约数
我们知道一个定理：
两个数a，b的乘积等于的最大公约数gcd（a，b）与最小公倍数lcm（a，b）的乘积
那么我们就可以运用这个性质来就最小公倍数lcm（a，b）=（a*b）/gcd（a，b）
6.质数判别
（1） sqrt判别
对于每一个质数n，我们都可以从2枚举到√n，如果都不能整除n，则n为质数
时间复杂度为O（√n）
局限性：只能判断少量的数据
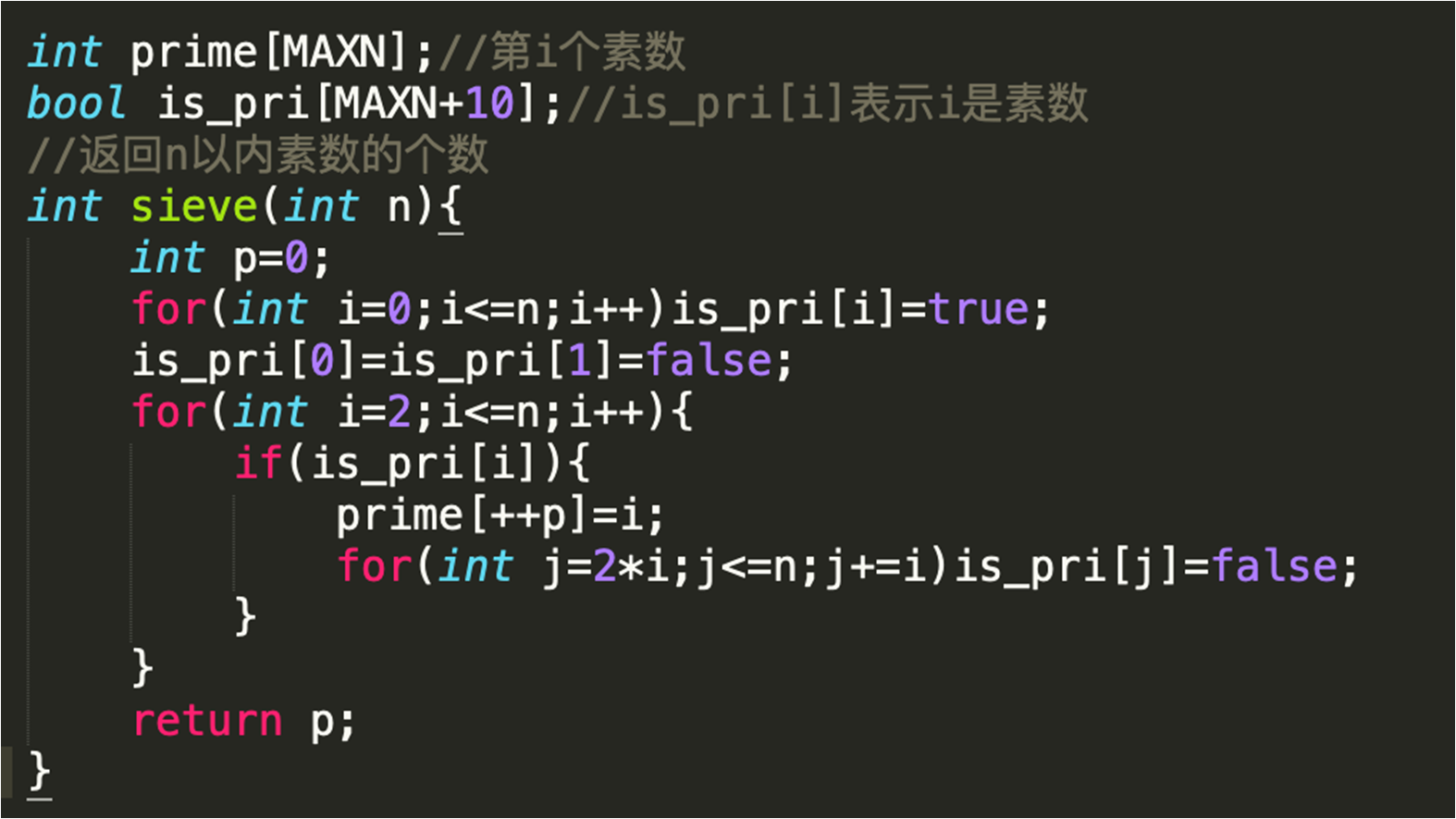
（2） 埃氏筛
判断n以内的数有哪几个数是质数，我们可以从2到n判断：
如果当前数为质数，那么将n的范围内把当前数的所有倍数都标记为合数；
如果当前数为合数，那么将n的范围内把当前数及所有倍数都标记为合数；
时间复杂度为O（n loglogn）
小缺点：有些合数可能被标记过多次（例如6就被2和3标记过），还可以优化一下
（3） 欧拉筛法——线性筛法
此筛法为埃氏筛的优化版，就是解决了一个数被多次标记的问题：
对于每一个合数，我们就让它被它最小的质因子标记一次
7.欧拉函数
是小于或等于n的正整数中与n互质的数的数目
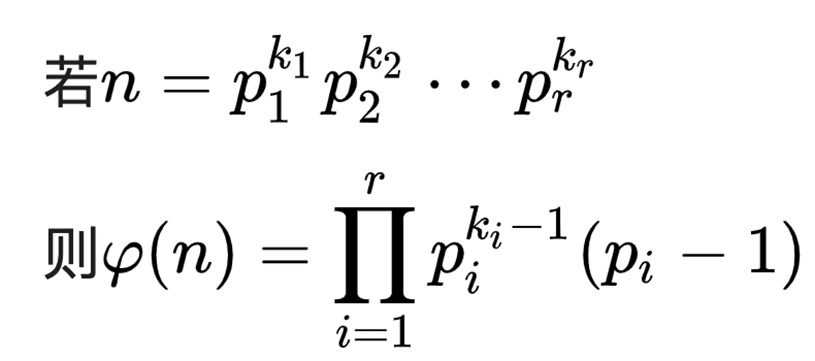
若n，a为正整数，且n，a互素，则
欧拉定理
8.矩阵乘法
一个m*n的矩阵就是m*n个数排列成m行n列的一个数阵
一个m*p的矩阵A乘一个p*n的矩阵B 得到一个m*n的矩阵，其中：
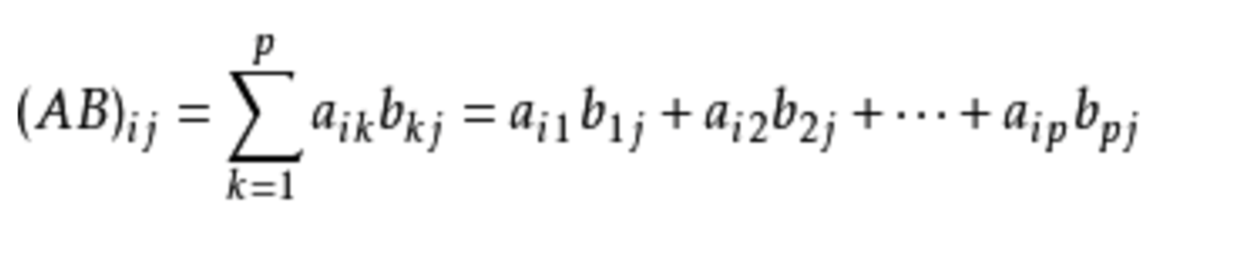
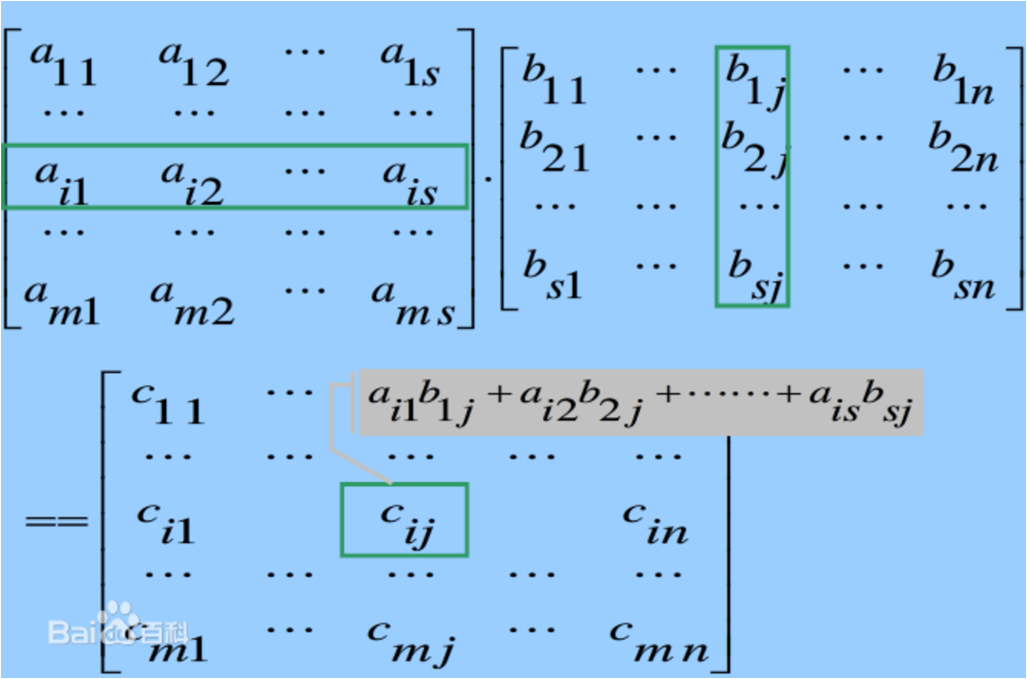
例如：
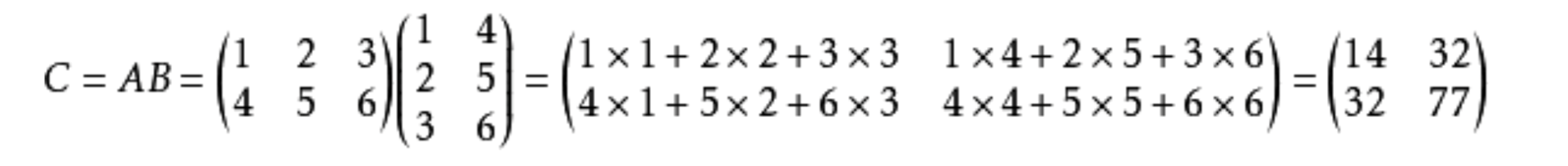
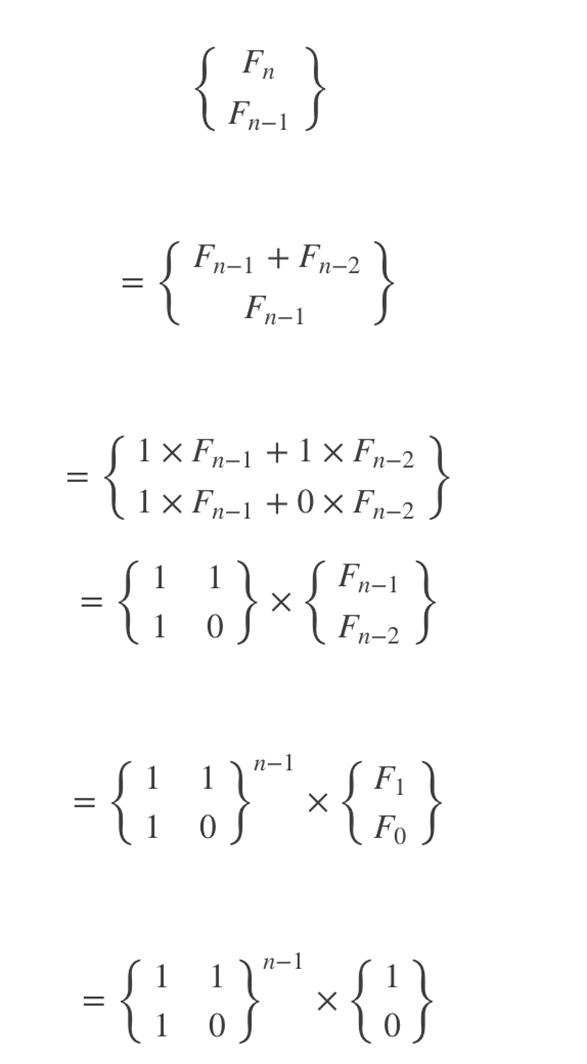
所以我们只要对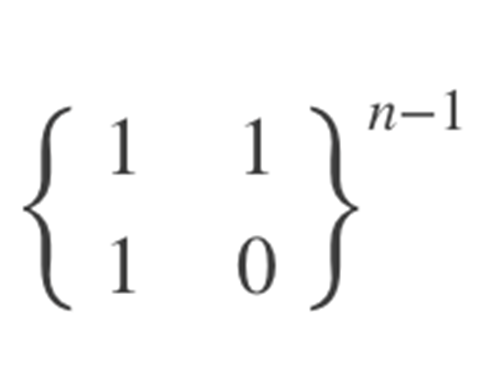
进行快速幂运算就好了
注意重载运算符，将*变为矩阵乘法，这样就可以快速幂啦
struct matrix{
int hang,lie;
lli data[101][101];
matrix() //我们给他一个构造函数初始化一下
{
hang=lie=0;
for (register int i=1;i<=100;i++)
for (register int j=1;j<=100;j++)
data[i][j]=0;
}
};
inline matrix operator * (const matrix &a,const matrix &b) //重载运算符，这样就可以将矩阵进行普通的快速幂运算了，核心!!!
{
matrix c; //作为矩阵乘法答案
c.hang=a.hang; //因为答案的行数是和a矩阵的行对齐的
c.lie=b.lie; //因为答案的列数是和b矩阵的列对齐的
for (register int i=1;i<=c.hang;i++) //枚举每一项进行相加
{
for (register int j=1;j<=c.lie;j++)
{
//累加操作，注意多进行几次mod
for (register int m=1;m<=a.lie;m++)
{
//枚举a矩阵的每一列,b矩阵的对应行数就不用管了
c.data[i][j]+=a.data[i][m]*b.data[m][j]%mod;
//理解一下就是c的第i行第j列就是a矩阵的i行的每一个数字和对应的b矩阵的
//第j列的每一个对应数字的乘积相加
//所以就是上面那个式子
c.data[i][j]%=mod;
}
}
}
return c;//完成乘法返回答案数组
}
扩展：
例题1：
我们对原式进行化简：
这样我们只要算出A^3和A+A^2+A^3即可，方法就是上面的矩阵快速幂
例题2：
思路：我们可以将每一步看做是乘上一个矩阵，暂且叫这个矩阵为操作矩阵（具体什么矩阵根据有向图决定）
那么我们只要用一开始的矩阵data[A][B]*操作矩阵^k ，也就是要用到上面讲的矩阵快速幂啦
上三角矩阵
性质：平方后还是上三角矩阵；
分块矩阵
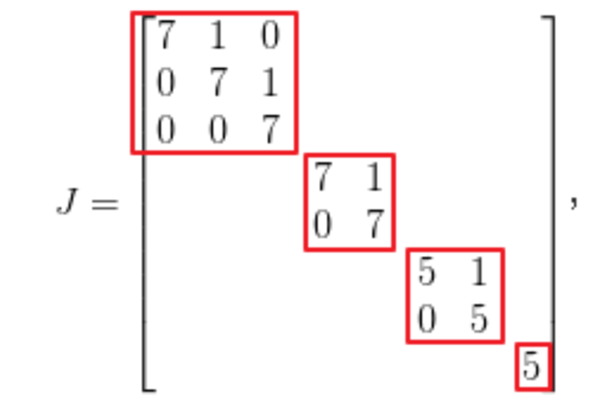
性质：平方后还是方块矩阵，且平方后对应位元素等于原位元素的平方；
对角矩阵
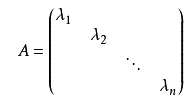
对称矩阵
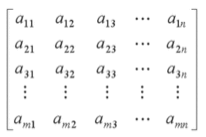
9.n元一次方程组
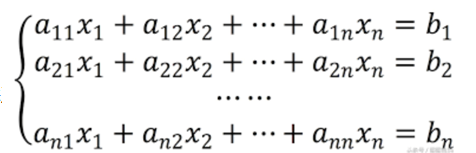
举个例子： 三元一次方程组
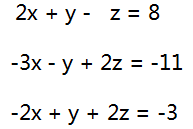
将每一未知数的系数以及等号后的b写成一个矩阵
这样我们将x，y，z的系数都消成1，那么答案就显而易见了：
x=2；y=3；z=-1；
无解的情况
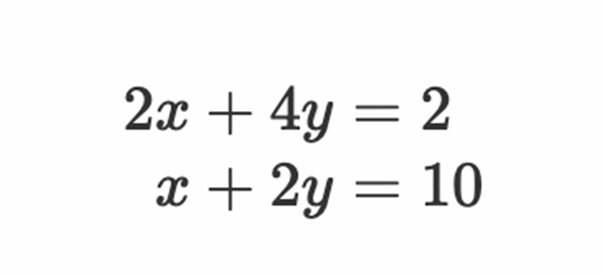
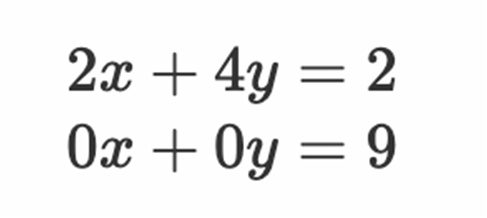
显然像这样就是无解的
无穷多解
像这样实质是一个方程的二元方程（就是不定方程）显然有无穷多个解
10.行列式
定义：
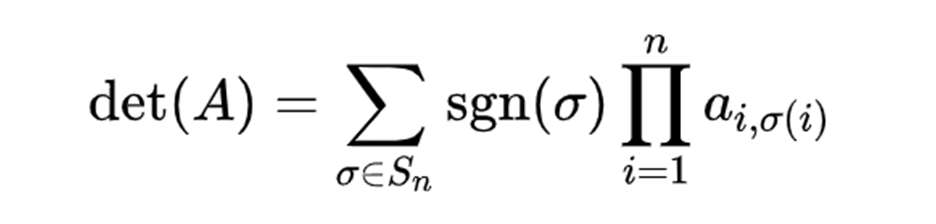
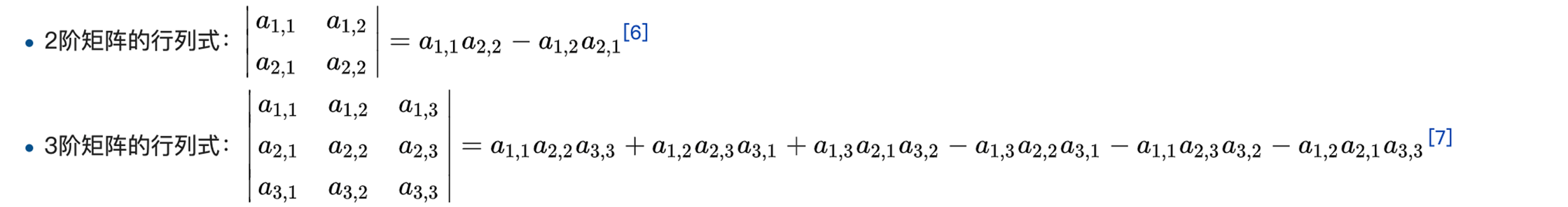
计算：
11.矩阵逆元
逆元的定义：
若矩阵B*A=I，则称B为A的左逆元
若矩阵A*B=I，则称B为A的右逆元
有逆元的前提： 矩阵的行列式不为0
如何求左逆元？？？
解： 设B*A=In In为单位矩阵（单位矩阵的性质：单位矩阵乘任何矩阵都为原矩阵）
接下来我们对A矩阵的任何操作，同样对In也操作一次
那么当A变为I时，In变为B
证：当A=>I时，原式变为： I*B=？
显然矩阵In变为了矩阵B
12.矩阵树定理 印象开始模糊，甚至完全消失，允许我复制一波课件
扩展：k^2*logn求常系数线性递推方程
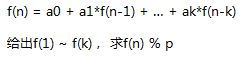
以斐波那契数为例：
洛谷2233
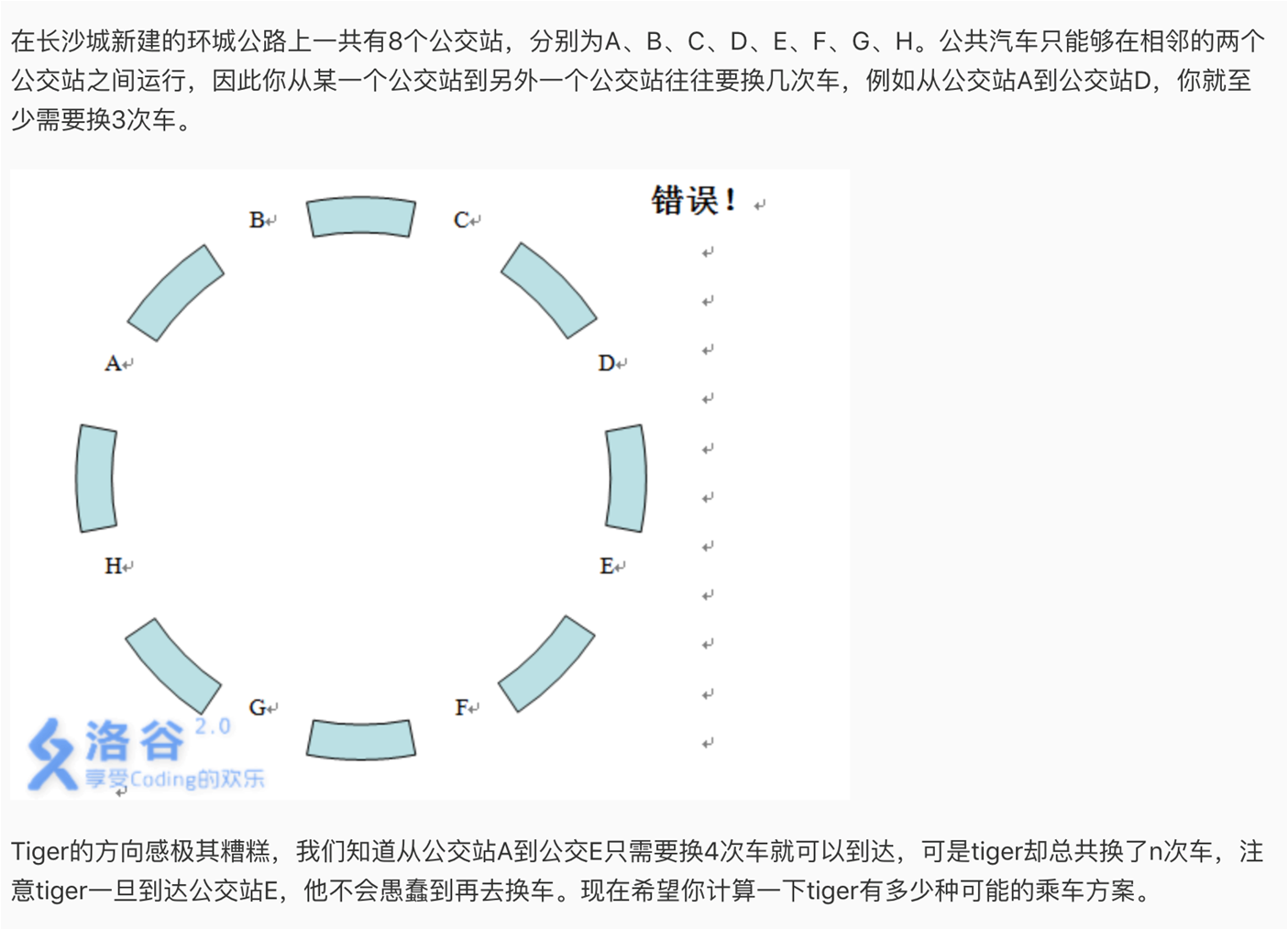
思路：我们知道到达D点是由C或E走过来的，我们不妨解决这个题的子问题：走n-1次正好走到C或E的方案数，且中途不经过D点
所以我们可以将路径看做是乘上下面的矩阵：
上面的1是表示可能到达A,B……E，第一行第一列代表A，第二行第二列代表B……依次类推
所以我们只要用矩阵快速幂求出这个矩阵^n-1次方就好啦
以上就是清北学堂第一天的内容啦！
内容好多啊QWQ