首先回顾上节课末尾引出来的VC Bound概念,对于机器学习来说,VC dimension理论到底有啥用。

三点:
1. 如果有Break Point证明是一个好的假设集合
2. 如果N足够大,那么Ein跟Eout的表现会比较接近
3. 如果算法A选的g足够好(Ein很小),则可能从数据中学到了东西
==================================================
现在正式引出VC Dimension的概念:啥叫VC Dimension:

VC Dimension是针对某个假设集合的一个性质。简言之,就是Break Point - 1的那个值的正式说法。如果没有Break Point,则VC Dimension是无限。
因此,VC Dimension有限被认为是好的。
为啥是好的呢?回顾之前几节的内容,有如下的结论证明VC Dimension有限是好的(样本充足情况下,可以保证Eout跟Ein接近)

马上举一个例子,证明VC Dimension的用处:

对于2D PLA来说:
1. 如果是linear separable D , 则迭代次数足够,一定可以得到Ein(out)是0 (从训练集学到了东西)
2. 二维平面上 binary classification的VC Dimension是3,因此N足够大时候,Ein与Eout很接近(训练集的学习效果可以迁移到测试集)
端午放假出去散心。。。回来接着写。。。。
=======================================================================
在分析了1D perceptron和2D perceptron之后,猜测是否d-D perceptron的VC Dimension是d+1维呢?(这个猜测是可以证明成立的)
需要证明如下的式子:

先从第一个开始:
需要证明N=d+1时,某些情况下是可以shatter的即可。课件中举了这个例子:

举了这个例子,因为矩阵X是可逆的,不管Y的d+1维分量怎么取值(取0或1)组合,都可以求出来这样一个W。所以,证明了有些情况下d+1个inputs是可以被shatter的。
到这里,对可逆是咋回事已经要忘记了。
翻了翻课件(矩阵分析课程的):

那么林的课件中的矩阵是依据啥构造出来的呢?我觉得是依据“A的行/列线性无关”这一条等价的性质构造出来的。
线性相关、无关是啥啊?
再翻一翻课件:

跟记忆中的差不多。
矩阵各种性质和运算操作太重要了,但是不想打断林这个课程的学习。搜到一个Brown大学的矩阵程序开发课程https://www.coursera.org/course/matrix,用python编写矩阵的各种操作,后续一定补上。
再证明后半部分:

1. 如果输入是d+2维的,那么一定可以构造出来第d+2个行向量是1~d+1个行向量的线性表示
2. 这时,如果WTX1~WTXd+1与其前面的系数a1~ad+1同号,则等式一定是大于零的;
3. 因此这个时候Yd+2就一定得是1,不可能取到0;也就是说,当Y1~Yd+1的取值跟a1~ad+1同号的情况下,Yd+2符号是定死的,所以Yd+2取不全01,因此无法shatter
下面看了DC Dimension的physical intuition
"effective binary" degree of freedom

可以粗略地理解为:free parameters
更深入了解一下VC Dimension的意义,主要从VC Bound入手。
可以集成到下面几张PPT中:
1. VC Bound是对模型复杂度的一个惩罚项
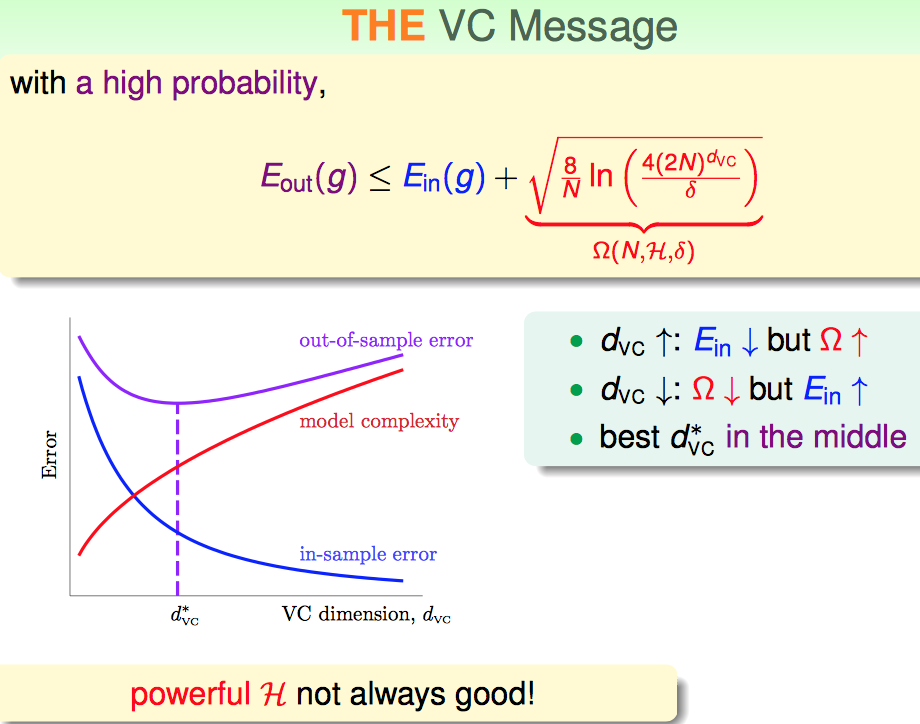
2. 可以根据VC Dimension来确定需要多大的样本量(实际经验一般是10倍的OK的)

3. VC Bound虽然是个非常宽松的Bound,但是却是一个通用性很强的Bound.
