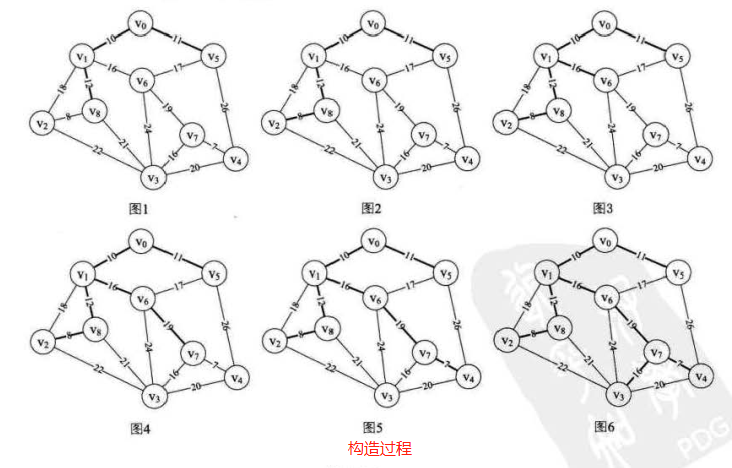
最小生成树:
我们把构造连通网的最小代价生成树称为最小生成树。经典的算法有两种,普利姆算法和克鲁斯卡尔算法。
普里姆算法打印最小生成树:
先选择一个点,把该顶点的边加入数组,再按照权值最小的原则选边,选完最小权值的边,把在所选边的另一顶点的边加入数组,再选权值最小的边,如此循环(有多少顶点循环多少次)
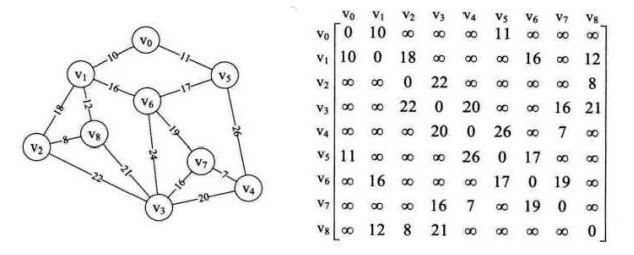
∞ 我们代码中用65535表示
//定义邻接矩阵 let Arr2 = [ [0, 10, 65535, 65535, 65535, 11, 65535, 65535, 65535], [10, 0, 18, 65535, 65535, 65535, 16, 65535, 12], [65535, 65535, 0, 22, 65535, 65535, 65535, 65535, 8], [65535, 65535, 22, 0, 20, 65535, 65535, 16, 21], [65535, 65535, 65535, 20, 0, 26, 65535, 7, 65535], [11, 65535, 65535, 65535, 26, 0, 17, 65535, 65535], [65535, 16, 65535, 65535, 65535, 17, 0, 19, 65535], [65535, 65535, 65535, 16, 7, 65535, 19, 0, 65535], [65535, 12, 8, 21, 65535, 65535, 65535, 65535, 0], ] let numVertexes = 9, //定义顶点数 numEdges = 15; //定义边数 // 定义图结构 function MGraph() { this.vexs = []; //顶点表 this.arc = []; // 邻接矩阵,可看作边表 this.numVertexes = null; //图中当前的顶点数 this.numEdges = null; //图中当前的边数 } let G = new MGraph(); //创建图使用 //创建图 function createMGraph() { G.numVertexes = numVertexes; //设置顶点数 G.numEdges = numEdges; //设置边数 //录入顶点信息 for (let i = 0; i < G.numVertexes; i++) { G.vexs[i] = 'V' + i; //scanf('%s'); //ascii码转字符 //String.fromCharCode(i + 65); } console.log(G.vexs) //打印顶点 //邻接矩阵初始化 for (let i = 0; i < G.numVertexes; i++) { G.arc[i] = []; for (j = 0; j < G.numVertexes; j++) { G.arc[i][j] = Arr2[i][j]; //INFINITY; } } console.log(G.arc); //打印邻接矩阵 } function MiniSpanTree_Prim() { let min, i, j, k; let adjvex = []; // 保存相关顶点下标 let lowcost = []; // 保存相关顶点间的权值 for (i = 0; i < G.numVertexes; i++) { lowcost[i] = G.arc[0][i]; //将V0顶点与之有边的权的权值存入数组 adjvex[i] = 0; //初始化都为v0的下标 } for (i = 1; i < G.numVertexes; i++) { min = 65535; j = 0; k = 0; while (j < G.numVertexes) { if (lowcost[j] != 0 && lowcost[j] < min) { //如果权值不为0且小于min min = lowcost[j]; k = j; } j++; } lowcost[k] = 0; //将当前顶点的权值设置为0,表示此顶点已完成任务 // console.log('(%d,%d,%d)', adjvex[k], k, min); //打印当前顶点边中权值最小边,和权值 console.log('(%s,%s,%d)', G.vexs[adjvex[k]], G.vexs[k], min); //打印顶点名称和权值 for (j = 0; j < G.numVertexes; j++) { //循环所有顶点 if (lowcost[j] != 0 && G.arc[k][j] < lowcost[j]) { //若下标为k顶点各边权值小于此前这些顶点未被加入生成树权值 lowcost[j] = G.arc[k][j]; //将较小权值存入 lowcost adjvex[j] = k; } } } } createMGraph(); console.log('**********打印最小生成树*********'); MiniSpanTree_Prim();
运行结果:
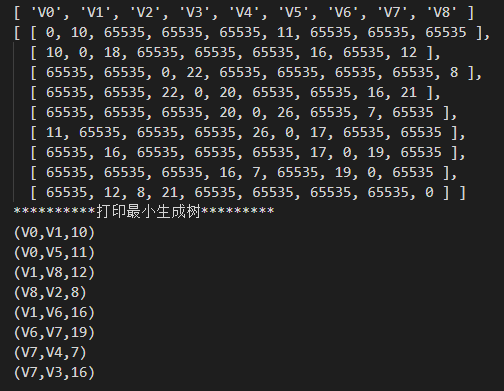
构造过程如下图加粗黑线: