golang广度优先算法-走迷宫

广度优先遍历，走迷宫思路：

1、创建二维数组，0表示是路，1表示是墙；创建队列Q，存储可遍历的点，Q的第一个元素为起始点

2、从队列中取一个点，开始，按上、左、下、右的顺序遍历周围的点next，next点在数组的范围内，且值为0，则把next存入队列Q中，并在steps（行走记录二维数组）中记录步数，该点周围的四个点遍历完后,从Q中取下一个点，重复以上步骤，直到Q中没有点或者当前点为终点为止

3、最后打印steps即为迷宫路线

代码：

package main

import (
    "fmt"
    "os"
)

type point struct {
    i, j int
}

//获取临近的点
func (p point) add(r point) point {
    return point{p.i + r.i, p.j + r.j}
}

//判断点是否在二维数组中，并返回点的值
func (p point) at(grid [][]int) (int, bool) {
    if p.i < 0 || p.i >= len(grid) {
        return 0, false
    }
    if p.j < 0 || p.j >= len(grid[p.i]) {
        return 0, false
    }
    return grid[p.i][p.j], true
}

//点的遍历顺序，上、左、下、右
var dirs = [4]point{
    {-1, 0}, {0, -1}, {1, 0}, {0, 1},
}

func walk(maze [][]int, start, end point) [][]int {

    steps := make([][]int, len(maze))

    for i := range steps {
        steps[i] = make([]int, len(maze[i]))
    }

    Q := []point{start}

    for len(Q) > 0 {
        cur := Q[0]
        Q = Q[1:]

        if cur == end {
            break
        }

        for _, dir := range dirs {
            next := cur.add(dir)

            val, ok := next.at(maze)

            //next点在数组中，且不能为墙 ，next点不能是起点
            if !ok || val != 0 {
                continue
            }

            if next == start {
                continue
            }

            if steps[next.i][next.j] == 0 && next.i <= end.i && next.j <= end.j {
                curSteps, _ := cur.at(steps)
                steps[next.i][next.j] = curSteps + 1
                Q = append(Q, next)
            }

        }
    }
    return steps
}

func readMaze(fileName string) [][]int {
    file, _ := os.Open(fileName)

    defer file.Close()
    var row, col int
    fmt.Fscanf(file, "%d %d", &row, &col)

    maze := make([][]int, row)
    for i := range maze {
        maze[i] = make([]int, col)
        for j := range maze[i] {
            fmt.Fscan(file, &maze[i][j])
        }
    }
    return maze
}

func main() {

    maze := readMaze("arr.in")
    steps := walk(maze, point{0, 0}, point{len(maze) - 1, len(maze[0]) - 1})
    for _, row := range steps {
        for _, val := range row {
            fmt.Printf("%3d ", val)
        }
        fmt.Println()
    }
}

打印结果：

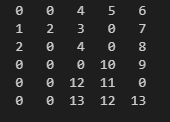
arr.in文件内容

6 5
0 1 0 0 0
0 0 0 1 0
0 1 0 1 0
1 1 1 0 0
0 1 0 0 1
0 1 0 0 0