1.递归的简介
程序调用自身的编程技巧称为递归( recursion)。递归做为一种算法在程序设计语言中广泛应用。 一个过程或函数在其定义或说明中有直接或间接调用自身的一种方法,它通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解,递归策略只需少量的程序就可描述出解题过程所需要的多次重复计算,大大地减少了程序的代码量。递归的能力在于用有限的语句来定义对象的无限集合。
递归的三个条件:
1.边界条件
2.递归前进段
3.递归返回段
当边界条件不满足时,递归前进;当边界条件满足时,递归返回。
2.递归的实例
2 /** 3 * 4 * <p>Title: Test2.java</p> 5 * <p>Description:递归的练习 </p> 6 * <p>Company: 中国农业银行</p> 7 * @author 二少爷 8 * @date 2018年6月5日 9 */ 10 public class Test2 { 11 12 /** 13 * 阶乘 14 * @param args 15 */ 16 public static int f(int i){ 17 if (i==0) { 18 return 1; 19 } 20 if (i>=1) { 21 return i*f(i-1); 22 } 23 return f(i); 24 25 } 26 27 /** 28 * 斐波那契数列 29 * @param n 30 * @return 31 */ 32 public static int j(int n){ 33 if(n==1||n==2){ 34 return 1; 35 } 36 if(n>2){ 37 return j(n-1)+j(n-2); 38 } 39 return 0; 40 } 41 public static void main(String[] args) { 42 int i = f(6); 43 System.out.println(i); 44 45 System.out.println("========"); 46 int n = j(7); 47 System.out.println(n); 48 } 49 }
结果图
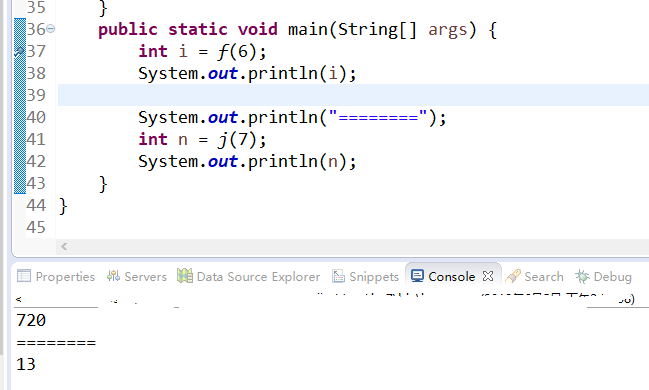
3.汉诺塔题型
1 /** 2 * 3 * <p>Title: Test3.java</p> 4 * <p>Description: 汉诺塔问题</p> 5 * <p>Company: 中国农业银行</p> 6 * @author 二少爷 7 * 8 */ 9 public class Test3 { 10 11 /** 12 * 移动的总数 13 * @param x 14 * @param a 15 * @param b 16 * @param c 17 * @return 18 */ 19 20 static int count = 1; 21 public static void solve(int x,String a,String b,String c){ 22 23 if (x==1) { 24 move(1,a,c); 25 26 } 27 if (x>=2) { 28 solve(x-1,a,c,b); 29 move(x,a,c); 30 31 solve(x-1,b,a,c); 32 33 } 34 35 } 36 public static void move(int x,String a,String b){ 37 38 System.out.print("从"+ a +"移动第"+ x +"个盘子到"+ b); 39 40 System.out.println(",这是第"+ count +"次移动."); 41 count +=1; 42 43 } 44 public static void main(String[] args) { 45 int x=3; 46 47 solve(x,"a","b","c"); 48 49 } 50 }
结果图
