基于稀疏表(Sparse Table)的RMQ需要先进行复杂度O(nlogn)的预处理,而后在查询[ql, qr]的最值时,计算出最大的满足ql + (1 << bit) <= qr的bit(复杂度O(loglogn)),即可在O(1)时间复杂度内查询,从而可以解决查询次数很多(如大于100万)的RMQ问题。
我们定义t[i][j]为以 i 为左端点的长度为 2j 的闭区间(0 <= j, 2j <= n, 1 <= i <= n - 2j + 1)
我们可以得到如下的一个稀疏表
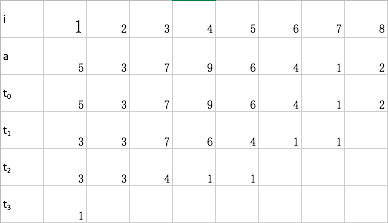
这样以来每个t[][]表示的都是一段长度为2的幂次的区间的最值。但考虑到实际查询的区间长度往往不是2的幂次,那么这个区间要如何表示呢?答案是一个不行,就来两个。把查询区间用两个区间的并来表示。为了确保两个区间的并恰好为查询区间,我们可以从左右边界向中间扫(如图)

那么为了确保两个小区间可以包含整个大区间,小区间长度必然不小于原区间的一半,且区间长度为2的幂次。所以在RMQ中,我们首先要求出满足2j <= qr - ql < 2j + 1 的j。也就是使得2j不超过(qr - ql)的最大的j。
有了这种划分区间的思想,我们可以轻易地出状态转移公式
t[i][j] = {t[i][j - 1], t[i + (1 << (j - 1))][j - 1]};
对于每个查询,{dp[ql][j], dp[qr - (1 << j) + 1][j])就是答案了。//左右皆闭
这样以来问题就仅剩下,如何高效地求解对应j呢?
计算(qr - ql),然后二分求解即可

1 int mbit(int a) { 2 int l = 0, r = 16; 3 while (l < r - 1) { 4 int m = (l + r) / 2; 5 if ((1 << m) <= a) { 6 l = m; 7 } else { 8 r = m; 9 } 10 } 11 return l; 12 }
求解给定闭区间的最大值和最小值的题目

1 #include <cmath> 2 #include <cstdio> 3 #include <cstring> 4 #include <algorithm> 5 #include <queue> 6 #include <vector> 7 #define max(x, y) (x > y ? x : y) 8 #define min(x, y) (x > y ? y : x) 9 #define INF 0x3f3f3f3f 10 #define mod 1000000007 11 typedef long long LL; 12 using namespace std; 13 14 const int maxn = 5e4 + 5; 15 const int maxnn = 16; 16 17 int n, m, c[maxn]; 18 int MAX[maxn][maxnn]; 19 int MIN[maxn][maxnn]; 20 int ql, qr, b; 21 22 void init() { 23 for (int i = 1; i <= n; i++) { 24 MAX[i][0] = MIN[i][0] = c[i]; 25 } 26 double limit = log(n) / log(2.0); 27 for (int j = 1; j <= (int)limit; j++) { 28 for (int i = 1; i + (1 << j) - 1 <= n; i++) { 29 MAX[i][j] = max(MAX[i][j - 1], MAX[i + (1 << (j - 1))][j - 1]); 30 MIN[i][j] = min(MIN[i][j - 1], MIN[i + (1 << (j - 1))][j - 1]); 31 } 32 } 33 } 34 35 int mbit(int a) { 36 int l = 0, r = 16; 37 while (l < r - 1) { 38 int m = (l + r) / 2; 39 if ((1 << m) <= a) { 40 l = m; 41 } else { 42 r = m; 43 } 44 } 45 return l; 46 } 47 48 int getmax() { 49 return max(MAX[ql][b], MAX[qr - (1 << b) + 1][b]); 50 } 51 52 int getmin() { 53 return min(MIN[ql][b], MIN[qr - (1 << b) + 1][b]); 54 } 55 56 int main(int argc, const char * argv[]) { 57 scanf("%d%d", &n, &m); 58 for (int i = 1; i <= n; i++) { 59 scanf("%d", &c[i]); 60 } 61 init(); 62 while (m--) { 63 scanf("%d%d", &ql, &qr); 64 b = mbit(qr - ql); 65 printf("%d ", getmax() - getmin()); 66 } 67 return 0; 68 }
下标是从0开始的,所以处理成了区间左闭右开的形式,稍微有点不同

1 void init() { 2 for (int i = 0; i < n; i++) { // 3 MAX[i][0] = MIN[i][0] = c[i]; 4 } 5 double limit = log(n) / log(2.0); 6 for (int j = 1; j <= (int)limit; j++) { 7 for (int i = 0; i + (1 << j) - 1 < n; i++) { // 8 MAX[i][j] = max(MAX[i][j - 1], MAX[i + (1 << (j - 1))][j - 1]); 9 MIN[i][j] = min(MIN[i][j - 1], MIN[i + (1 << (j - 1))][j - 1]); 10 } 11 } 12 } 13 14 15 int getmax() { 16 return max(MAX[ql - 1][b], MAX[qr - (1 << b)][b]); // 17 } 18 19 int getmin() { 20 return min(MIN[ql - 1][b], MIN[qr - (1 << b)][b]); // 21 }
