1. 用2个stack sort numbers
给定一个stack1,里面的数是unsorted,只允许用额外一个stack2去sort这个stack。
分析思路如下:
- 一个global_min来放当前最小值(初始为stack1.pop()出来的值)
- 然后依次和stack1.pop()出来的值进行比较,如global_min<stack1.pop(),则把stack1.pop()的值压入stack2,继续比较;如global_min>stack1.pop(),则把global_min压入stack2,global_min换成stack.pop()
- 直到比完stack1最后一个值,再把第一轮最后的global_min压入stack1,此时的global_min为最小值
- 把stack2中的数再压回stack1
- 接着比下一轮时要注意,不是从stack1最底层开始比,要从stack1未sort好的部分开始比,即相当于每次压入global_min就在其后加一个挡板,之后的每一轮都从它之后的unsorted的数比较
- 一直重复,直到『挡板』移到stack1最后一个数
图示:

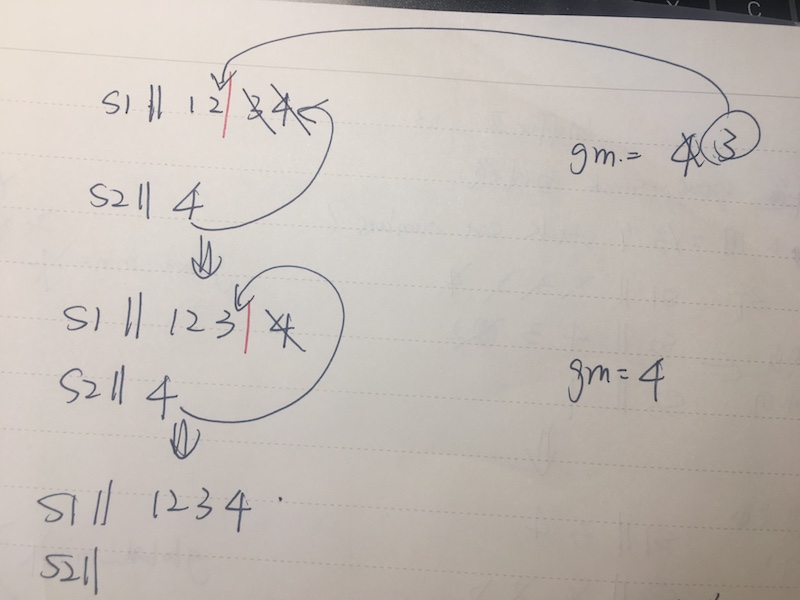
* 如果stack1里有很多重复的元素,有没有更优化的方案?
思路1:我们可以把和global_min重复的元素也放入stack2
思路2:使用counter,记录和global_min重复的元素,但是并不压入stack2,最后global_min压入stack1的时候,根据counter,压入等量的数
我们选择思路2:
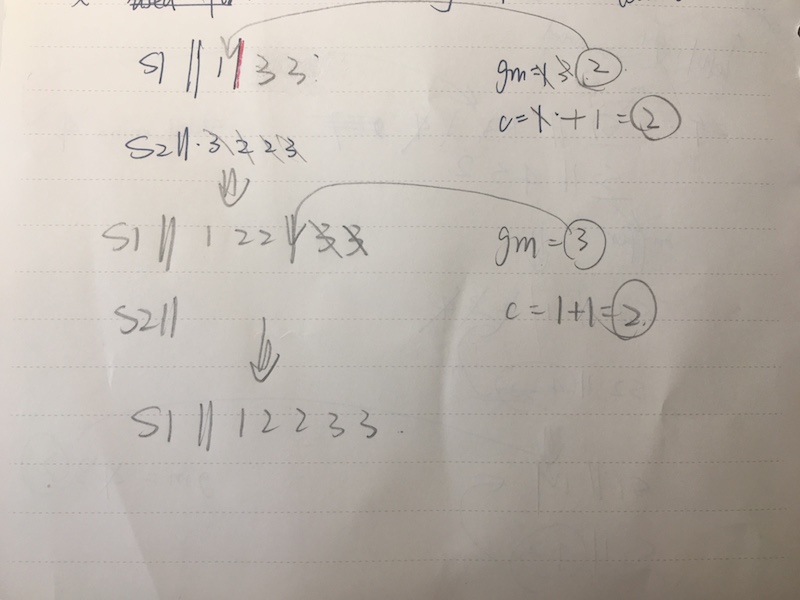
代码如下:
注意这里的stack是用LinkedList(参考LinkedList)实现的,所以这里的
peekFirst==peek
offerFirst==push
pollFirst==pop
可以看成是deque,但是只用一边进出
public class Solution { public void sort(LinkedList<Integer> s1) { LinkedList<Integer> s2 = new LinkedList<Integer>(); // Write your solution here. int n=s1.size(); sort_stack(s1,s2,n); } private void sort_stack(LinkedList<Integer> s1, LinkedList<Integer> s2, int size){ int i=0; while(i<size-1){ Integer global_max=s1.pollFirst(); int counter=1; for(int j=0;j<size-i-1;j++){ if(s1.peekFirst()<global_max){ s2.offerFirst(s1.pollFirst()); }else if(s1.peekFirst()==global_max){ s1.pollFirst(); counter+=1; }else{ for(int k=1; k<=counter;k++){ s2.offerFirst(global_max); } global_max=s1.pollFirst(); counter=1; } } for(int k=1; k<=counter;k++){ s1.offerFirst(global_max); } while(!s2.isEmpty()){ s1.offerFirst(s2.pollFirst()); } i++; } } }
2. 用两个stack实现一个queue
enqueue: (in)stack1: 用来存新的元素
dequeue: (out)stack2:用来pop:case1 如果stack2非空,直接pop —— O(1)
case2 如果stack2为空,先把所有的元素从stack1倒到stack2,再pop —— O(n)
我们来分析一下armotized time complexity of dequeue:
- 1st: n*stack1.pop()+n*s2.push()+1
- 2nd: 1
- 3rd: 1
- .
- .
所以:(2n+1+1*(n-1))/n=3=O(1)
(分子是underlying stack operations,分母是dequeue operations that we can support)
代码如下:

public class Solution { private Deque<Integer> stack1=new LinkedList<>(); private Deque<Integer> stack2=new LinkedList<>(); private void shuffle(){ while(!stack1.isEmpty()){ stack2.push(stack1.pop()); } } public Integer poll() { if(stack2.isEmpty()){ shuffle(); } if(stack2.isEmpty()){ return null; } return stack2.pop(); } public void offer(int element) { stack1.push(element); } public Integer peek() { if(stack2.isEmpty()){ shuffle(); } if(stack2.isEmpty()){ return null; } return stack2.peek(); } public int size() { return stack1.size()+stack2.size(); } public boolean isEmpty() { if(stack2.isEmpty() && stack1.isEmpty()){ return true; } return false; } }
*变种题1:两个queue实现一个stack
Q:->xxxxxx->
S: ->xxxxxx
<-
push(): 直接往Q1放
pop(): 把除了最后的元素都移到Q2,然后再Q1.pop()
然后直接换一下reference,下次就又可以直接操作Q1
此时Q2的作用相当于一个buffer
*变种题2:一个queue实现一个stack
此时我们要假设可以一直知道queue的size
push():直接从q push
pop(): 此时需要先把顶层前面的元素pop出来,然后从屁股push回去,直到把顶层元素压到最底层,pop出来
3. 用stack实现min() function
pop() push() top() min()
stack1:is used to store input elements
minstack:is used to store the min element so far in s1 (as its top elements)
TC=O(1)
SC=O(n)
要注意的是,minstake里的数要和stack1的同步,比如stack1pop出一个数,如果这个数也再minstack的顶上,我们也要pop出

public class Solution { public Solution() { // write your solution here } Deque<Integer> stack=new LinkedList<>(); Deque<Integer> minstack=new LinkedList<>(); public int pop() { if(stack.isEmpty()){ return -1; } Integer element=stack.pop(); if(element.equals(minstack.peek())){ minstack.pop(); } return element; } public void push(int element) { stack.push(element); if(minstack.isEmpty()||element<=minstack.peek()){ minstack.push(element); } } public int top() { if(stack.isEmpty()){ return -1; } return stack.peek(); } public int min() { if(stack.isEmpty() && minstack.isEmpty()){ return -1; } return minstack.peek(); } }
4. 用2或3个stack实现deque
deque:left.add() left.remove() right.add() right.remove()
1)用两个stack:头对头
-> ||s1 s2|| ->
<- <-
left.add()=s1.push()——O(1)
right.add()=s2.push()——O(1)
left.remove():如果S1非空,则直接S1.pop()——O(1)
如果S1为空,则把所有元素从S2移到S1,再S1.pop() ——O(n)
同理,right.remove()
那我们来算一下remove的amortized time
worst case应该是
L.remove(); ——2n+1
R.remove(); ——2(n-1)+1
L.remove(); ——2(n-2)+!
R.remove(); ——2(n-3)+!
……
amotized time=(2n+!+2(n-1)+1+……+1)/n=n
无法amortize成O(1)
2)三个strck来提高 remove的TC
S1和S2仍然作为左右手,而S3则作为一个buffer,来存放一半的元素
例如deque=5678
56||S1 S2||78
如果,初始状态为:
||S1 S2||5678
我们希望最后变成:
56||S1 S2||78
- 先把S2的一半7,8pop 出S2,压入S3:n/2 pop out of S2, n/2 push into S3
- 再把剩的一半pop出S2,压入S1:n/2 pop out of S2, n/2 push into S1
- 再把7,8压回S2:n/2 pop out of S3, n/2 push into S2
n/2*6=3n。之后的n/2个操作,我们只需要pop对应边的元素就行了
此时的amortized time=(3n+1*n/2)/(n/2)=7=O(1)
总结:
1. 什么时候需要往stack上考虑?
当需要从左到右scan一个array/string时,如果要不断的回头看左边最新的元素师
eg:逆波兰表达式:a*(b+c) -> abc+*
public class Solution { public int evalRPN(String[] tokens) { // Write your solution here Deque<Integer> stack=new LinkedList<>(); for(int i=0;i<tokens.length;i++){ if(tokens[i]!="+" && tokens[i]!="-" && tokens[i]!="*" && tokens[i]!="/"){ Integer op = Integer.valueOf(Integer.parseInt(tokens[i])); stack.push(op); }else{ int op1=stack.pop(); int op2=stack.pop(); int res=0; if(tokens[i]=="+"){ res=op1+op2; }else if(tokens[i]=="-"){ res=op2-op1; //顺序 }else if(tokens[i]=="*"){ res=op2*op1; }else{ res=op2/op1; } stack.push(res); } } return stack.pop(); } }
2. 常见性质:S1的所有元素倒进S2, S2的顺序完全reverse
S1->S2->S1顺序不变,amortized tc分摊到每一个move的元素时间为O(1)
