转载基础知识:
图:pixabay
原文来源:kdnuggets
作者:Jahnavi Mahanta
「机器人圈」编译:嗯~阿童木呀、多啦A亮
Jahnavi Mahanta是Deeplearningtrack的联合创始人,Deeplearningtrack是一个在线导师的数据科学培训平台。
人工神经网络(ANN)算法能够模拟人类大脑处理信息。接下来我们将为大家解释人脑和ANN如何进行工作的。
人工神经网络(ANN)使用大脑处理信息的方式为基础,以此进行开发可用于建模复杂模式和预测问题的算法。
首先,我们需要了解的是我们的大脑是如何进行信息处理的:
在我们的大脑中,有数十亿个称为神经元的细胞,它们以电信号的形式处理信息。神经元的树突接收来自外部的信息或刺激,并在神经元细胞体进行处理,将其转化为输出并通过轴突传到下一个神经元。下一个神经元可以选择接受或拒绝它,这主要取决于信号的强度。
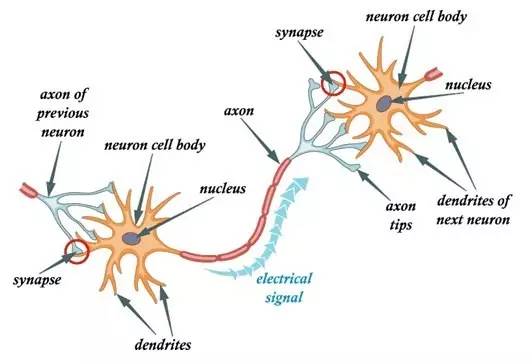

第一步:树突接触外部信号。
第二步:神经元处理外部信号。
第三步:处理的信号转化为输出信号并通过轴突传送。
第四步:输出信号通过突触由下一个神经的树突接收。
以上就是人类大脑进行信息处理的过程,接下来,我们试着了解一下ANN如何工作的:

现在,w1,w2,w3分别给出输入信号的强度。
正如你从上面可以看到的那样,ANN是一个非常简单的大脑神经元工作方式的表征。
为了使事情变得简单明了,让我们可以用一个简单的示例来帮助理解ANN:一家银行想评估是否批准一个客户的贷款申请,所以,它想要预测这个客户是否可能违约贷款。现在,它有如下数据:
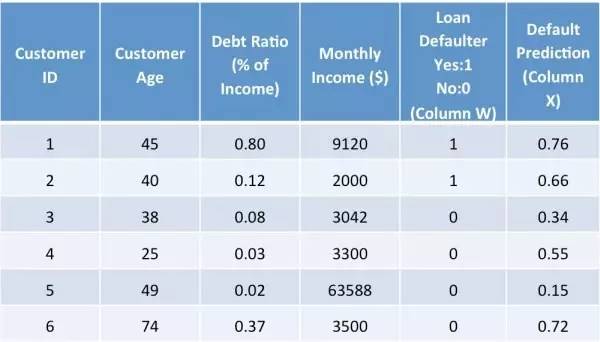
所以,我们必须预测第X列。预测结果越接近1就表明客户违约的机会越大。
我们可以使用这个示例,创建一个简单的基于神经元结构的人工神经网络结构:

通常而言,针对上述示例的简单ANN架构可以是这样的:

与架构有关的要点:
1.网络架构有一个输入层,隐藏层(可以是1层以上)和输出层。由于层数较多,因此也称之为MLP(多层感知器)。
2.隐藏层可以被看作是一个“蒸馏层”,从输入中抽出一些重要的模式,并将其传递到下一层上。它通过从输入中识别出重要的信息而排除冗余信息,从而使网络更加快速和高效。
3.激活函数有两个显著的目的:
它可以捕获输入之间的非线性关系。
它可以有助于将输入转换为更为有用的输出。
在上面的例子中,所使用的激活函数是sigmoid:
O1 = 1/1 + e-F
其中F = W1 * X1 + W2 * X2 + W3 * X3
Sigmoid激活函数创建一个值在0和1之间的输出。当然,其他激活函数,如Tanh,softmax和RELU也是可以用的。
4.类似地,隐藏层引起输出层的最终预测:
O3 = 1/1 + e-F 1
其中F 1 = W7 * H1 + W8 * H2
这里,输出值(O3)的范围在0和1之间。接近1(例如0.75)的值表示存在客户默认值较高。
5.权重W是与输入相关联的重要点。如果W1是0.56,W2是0.92,那么在预测H1时,X2:债务比率比X1:Age更重要。
6.上述网络架构称为“前馈网络”,你可以看到输入信号只在一个方向(从输入到输出)流动。我们还可以创建信号在两个方向上流动的“反馈网络”。
7.具有高精度的良好模型提供了非常接近实际值的预测。因此,在上表中,列X值应该非常接近于列W值。预测误差是列W和列X之间的差异:

8.获得具有准确预测的良好模型的关键是找到最小化预测误差的“W权重的最优值”。这是使用“反向传播算法”实现的,这使ANN成为一种学习算法,因为通过从错误中学习,模型得到了改进。
9.最常见的优化方法称为“梯度下降”,其中使用了迭代不同的W值,并对预测误差进行了评估。 因此,为了得到最优的W值,W值的变化很小,对预测误差的影响进行了评估。 最后,W的这些值被选为最优的,随着W的进一步变化,误差不会进一步降低。 要了解梯度下降的更详细的信息,请参考http://www.kdnuggets.com/2017/04/simple-understand-gradient-descent-algorithm.html
NOTE:
两个变量之间存在一次方函数关系,就称它们之间存在线性关系。正比例关系是线性关系中的特例,反比例关系不是线性关系。更通俗一点讲,如果把这两个变量分别作为点的横坐标与纵坐标,其图象是平面上的一条直线,则这两个变量之间的关系就是线性关系。即如果可以用一个二元一次方程来表达两个变量之间关系的话,这两个变量之间的关系称为线性关系,因而,二元一次方程也称为线性方程。推而广之,含有n个变量的一次方程,也称为n元线性方程