题面
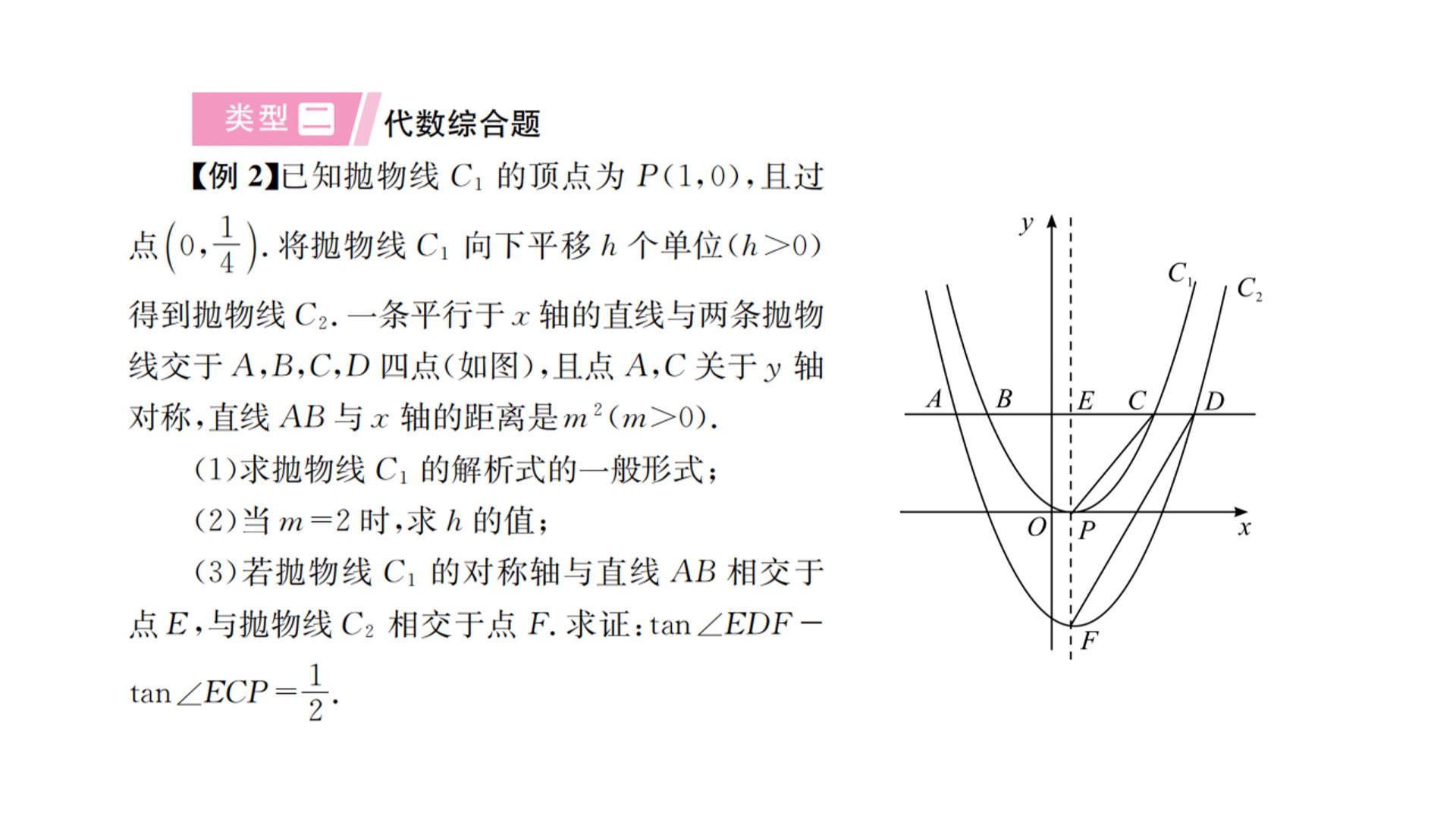
需要说的是书上好像打错了
第一问
我们注意到题目给出了
你要相信出题人绝不会放水他只会放海
于是我们列出顶点式:(y=a(x-1)^2)
然后意外加惊喜地发现还有一个点(0,(frac{1}{4}))可用
这不就可以解了吗
(a(0-1)^2=frac{1}{4}),解得(a=frac{1}{4})
化成一般式为:
(y=frac{1}{4}x^2-frac{1}{2}x+frac{1}{4})
总结:一个顶点+另一个点=抛物线解析式
第二问
让我们注意一下这句话:
将抛物线(C_1)向下平移(h)个单位得到抛物线(C_2)
得出的结论:(C_2):(y=frac{1}{4}(x-1)^2-h)
(向下平移,只有常数项c会改变)
注意这个结论,对理解第三问的法二有帮助
继续讲解
直线(AB)到(x)轴距离为(m^2)
(m=2),所以距离为(2^2=4),因此得出点(ABCD)的纵坐标都为4
由于(B)、(C)所处的抛物线(C_1)是已知的,就从(B)、(C)入手
(C_1):(y=frac{1}{4}(x-1)^2=4)
(x_1=5),(x_2=-3),所以(C(5,4))
A,C关于(y)轴对称,故(A(-5,4))
把(A(-5,4))代入(C_2),解得h=5
总结:我们可以尝试从已知处多、关联性强的地方进行突破
第三问
气氛突然苏维埃有趣了起来
这种题比较容易让人乍看之下一头雾水满脑糨糊
先分析题目
题目要求证tan∠EDF-tan∠ECP=(frac{1}{2})
值得注意的一点:
tan∠A-tan∠B≠tan(∠A-∠B)
不知道有没有人这么做反正不关我事
然后怎么办呢?
看看第二问的总结:我们可以尝试从已知处多、关联性强的地方进行突破
此题没有能一步推出的数据,但不妨碍我们找到能一步推出的关系
于是方法一上场
方法一
从第二问的推导过程中,我们得出:ABCD四个点,知道一个横坐标,就能推出另三个
由于B、C都在(C_1)上,不妨直接用(C_1)解析式中的(x)代入求值
从题目中可推出纵坐标为(m^2)
所以方程为(y=frac{1}{4}(x-1)^2=m^2)
直接开方即可解得(x_1=1+2m),(x_2=1-2m)
于是(C(1+2m,m^2)),又AC关于(y)轴对称,所以(A(-1-2m,m^2)),AE=ED=2+2m
拿到了点A,代入(C_2)的方程:
(y=frac{1}{4}(x-1)^2-h)
(=frac{1}{4}[(-1-2m)-1]^2-h=m^2)
解得h=2m+1 ,所以EF=(h+m^2)=(m^2+2m+1)
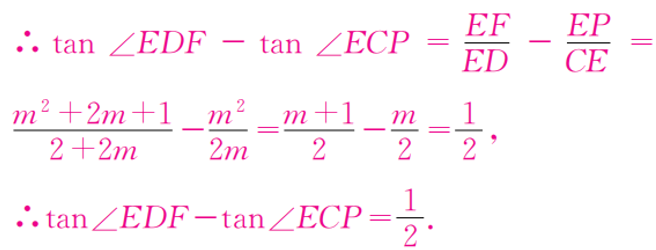
总结:没有数据可推时,可以选择推出未知数间的关系
方法二
先介绍一个引理
引理:二次函数中,△x与△y的关系只由二次项系数a决定
证明:因为图像形状只由二次项系数a决定,老师上课讲过
思维小跳跃预警
设CE为x,则PE=(frac{1}{4}x^2)(引理,可将PE视作△y)
由对称可得CD=2
得ED=(x+2)
列出方程:
(frac{1}{4}(x+2)^2-frac{1}{4}x^2=h)
解释:另行解释
解得h=x+1,即PF=x+1
tan∠EDF-tan∠ECP=(frac{frac{1}{4}x^2+(x+1)}{x+2}-frac{frac{1}{4}x^2}{x})=(frac{1}{2})
得证
总结:上方引理