组合数学专题

NC19788 Travel

题意为：将n个节点的树分成m个连通块，并对每个连通块标号的方案数。

思路：初看这道题像树形dp，但一想转移方程和数据范围，感觉不可解。
换成组合数学的角度，将分成m个连通块转化为删去m-1条边，显然删去m-1条边的方案与分成m个连通块的方案是一一对应的，再将连通块标号，就是乘m的阶乘了。
C（n-1，m-1）×m！

NC50039 kotori

题意：n个1-m之间的数排成一排，相邻数不能相等的方案数。

思路：直接给公式：m×pow（m-1，n-1）

关键是扩展：n个1-m之间的数排成一个圆，相邻数不能相等的方案数。

同样的断链成环

https://www.luogu.com.cn/problem/P1357

#include <iostream>
#include <cstring>
#define inf 2147483647
#define ll long long
using namespace std;

const ll mo=1e9+7;
ll n,m,k,N; 
ll ans[33][33],w[33][33],a[33][33];
//f0[i][j]：首项是0，到了第i项时为j的条件方案数。 


void mi()
{
	ll kp[33][33]={0};
	for (int i=0;i<N;i++)	for (int j=0;j<N;j++) {
		kp[i][j]=0;
		for (int k=0;k<N;k++) kp[i][j]=(kp[i][j]%mo+ans[i][k]*w[k][j]%mo)%mo;
	}
	for (int i=0;i<N;i++)
	for (int j=0;j<N;j++) ans[i][j]=kp[i][j];
}

void zc()
{
	ll kp[33][33]={0};
	for (int i=0;i<N;i++) for (int j=0;j<N;j++)
	{	kp[i][j]=0;
		for (int k=0;k<N;k++) kp[i][j]=(kp[i][j]%mo+w[i][k]*w[k][j]%mo)%mo;
	}
	for (int i=0;i<N;i++)
	for (int j=0;j<N;j++) w[i][j]=kp[i][j];
}

void ksm(ll k)
{
	for (int i=0;i<N;i++) ans[i][i]=1; 
	while (k){ if (k&1) mi(); k/=2; zc(); }
}

int check(int x)  //初赛学到的可快速算二进制中1的函数. 
{	int sm=0;
	while (x){ x= x&(x-1); sm++; }
	return sm;
}

int main()
{
	cin>>n>>m>>k; N=(1<<m);
	for (int i=0;i<N;i++) if (check(i)<=k)  //预处理构造矩阵 
	{
		int j=i>>1; w[j][i]=1; 
		j|=(1<<(m-1)); if (check(j)<=k) w[j][i]=1;
	}
	ksm(n); ll sm=0;
	for (int i=0;i<N;i++) 
		if (check(i)<=k) sm=(sm+ans[i][i])%mo;
	cout<<sm<<endl;
}

NC14735 美丽的项链

就是一个基础dp

#include<stdio.h>
#include<string.h>
const int maxn=100;
#define max(a,b) a>b?a:b
int n,m,a[maxn],l[maxn],r[maxn];
long long dp[maxn][maxn+1];
int main(){
    int i,j,k;
    //freopen("input.txt","r",stdin);
    while(~scanf("%d%d",&n,&m)){
        for(i=0;i<n;i++) scanf("%d%d",l+i,r+i);
        memset(dp,0,sizeof(dp));
        for(i=l[0];i<=r[0];i++) dp[0][i]=1;
        for(i=1;i<n;i++)
            for(j=1;j<=m;j++){
                int left=max(0,j-r[i]),right=max(0,j-l[i]);
                for(k=left;k<=right;k++) dp[i][j]+=dp[i-1][k];
            }
        printf("%lld\n",dp[n-1][m]);
    }
}//dp[i][j]表示用前i种宝石组成j颗宝石的项链的方案数
 //但是第i种只能是l[i]到r[i]之间的数量
 //所以dp[i][j]=dp[i-1][j-r[i]]+dp[i-1][j-r[i]+1]+...+dp[i-1][j-l[i]]

NC15251 白兔的式子

NC14599 子序列

NC15550 箱庭的股市

NC16543 NC20824

NC15077

https://ac.nowcoder.com/acm/problem/15077

因为要保证一定经过该点 所以将路线图分为两部分的卡特兰数

这个是我高中数学老师张刚讲组合数的时候讲的方法 我印象很深

NC16537

【C++】球盒问题总结（八种情况）https://blog.csdn.net/Ljnoit/article/details/102211595

namespace CNM {//组合数板子
    const int N = 2e6 + 5;
    ll quick(ll x, ll n)
    {
        ll res = 1;
        while (n)
        {
            if (n & 1) res = (res*x) % mod;
            x = x * x%mod;
            n >>= 1;
        }
        return res;
    }
    ll inv(ll x) { return quick(x, mod - 2); }
    ll fac[N], invfac[N];
    void init()
    {
        fac[0] = 1;
        for (int i = 1; i < N; ++i) fac[i] = (fac[i - 1] * i) % mod;
        invfac[N - 1] = inv(fac[N - 1]);
        for (int i = N - 2; i >= 0; --i) invfac[i] = (invfac[i + 1] * (i + 1)) % mod;
    }
    ll C(int n, int m)
    {
        if (n < m || m < 0) return 0;
        return fac[n] * invfac[m] % mod*invfac[n - m] % mod;
    }
}
vector<pair<int,int>> fac[MAXN];
int x, y;
void slove() {
    cin >> x >> y;
    ll ans = 1;
    for (auto p : fac[x]) {
        int n = p.second, m = y;
        ans *= CNM::C(n + m - 1,m - 1);
        ans %= mod;
    }
    ans *= ksm(2, y - 1, mod);
    ans %= mod;
    cout << ans << endl;
}
signed main() {
    CNM::init();
    for (int i = 2; i < MAXN; i++) {
        if (fac[i].size())continue;
        for (int j = i; j < MAXN; j += i) {
            int t = j, cnt = 0;
            while (t%i == 0)t /= i, cnt++;
            fac[j].push_back({ i,cnt });
        }
    }
    IOS;
    int T; cin >> T;
    while(T--)slove();
}

https://ac.nowcoder.com/acm/problem/14599

#include <cstdio>
#include <iostream>
#include <cstring>
#define int long long
const int N     = 1e6+10;
const int MOD   = 1000000007;
using namespace std;
 
long long bin[N];
void Init()
{
    bin[0]=1;
    bin[1]=1;
    for(int i=2;i<N;i++)
        bin[i]=i*bin[i-1]%MOD;
}
long long POW(long long a,long long b)
{
    long long res=1;
    while(b)
    {
        if(b&1)
        {
            res*=a, res%=MOD;
        }
        b>>=1;
        a*=a, a%=MOD;
    }
    return res;
}
long long C(long long n, long long m)//求C(n,m) n在下，m在上。注意在这之前加init函数
{
    return (bin[n]%MOD)*(POW(bin[m]*bin[n-m]%MOD,MOD-2))%MOD;
}
 
char str[N];
int n, m;
 
void Solve()
{
    int ans = 0;
    for (int i=1; i<=m-n+1; i++)
    {
        ans += C(m-i,n-1) * POW(25, m-i-n+1) % MOD * POW(26, i-1) % MOD, ans%=MOD;
    }
    printf("%lld\n",ans);
}
 
signed main()
{
    Init();
    scanf("%s",str+1);
    n = strlen(str+1);
    scanf("%lld",&m);
    Solve();
    return 0;
}

牛客33187K多校 - Link with Bracket Sequence I

   dp[0][0][0] = 1;
	for (int i=1; i<=m; i++)
	{
		for (int j=0; j<=i; j++)
		{
            //从你决定开始匹配S第一个字符之前，放什么都行（只要左括号数量>=右括号）
			dp[i][0][j] += (j-1<0?0:dp[i-1][0][j-1]) + dp[i-1][0][j+1], dp[i][0][j]%=MOD;
		}
	}
	
	for (int i=1; i<=m; i++)
	{
		for (int j=1; j<=min(m, n); j++)
		{
			for (int k=0; k<=i; k++)
			{
				int d = -1 + 2*(str[j]=='(');//左括号为1，右括号为-1

            //对于T的第 i 个字符，有两种情况：
            //一种是第i个字符匹配上原串的第j个字符，有1种放法
            //一种是第i个字符在前i-1个已经匹配上原串的第j个字符的情况下，有1种放法。
				if(k-d>=0)	dp[i][j][k] += dp[i-1][j-1][k-d];
				if(k+d<=m)	dp[i][j][k] += dp[i-1][j][k+d];
				dp[i][j][k] %= MOD;
			}
		}
	}
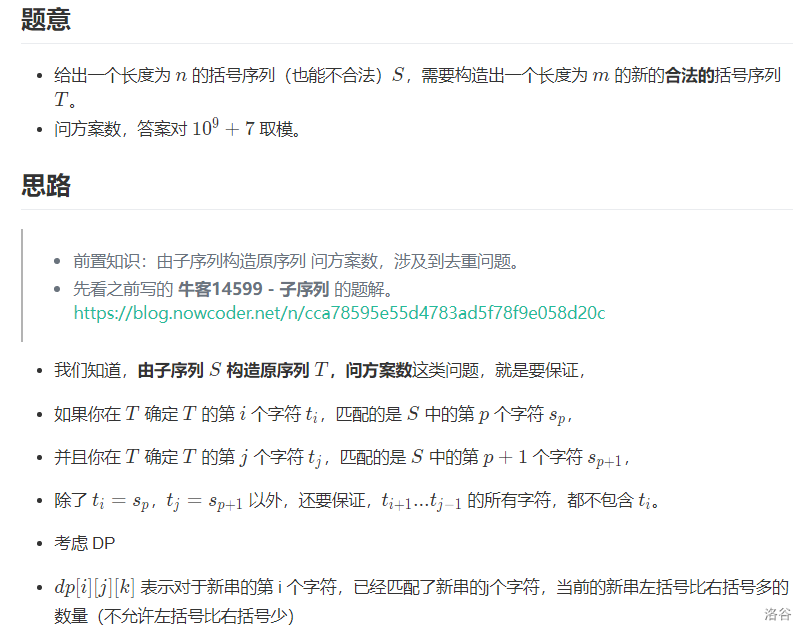
	printf("%lld\n",dp[m][n][0]);