

设不同方案数为cnt p=1/cnt 1/p=cnt
cnt=总方案数/重复的个数 这里就是一个简单的高中排列组合的知识
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define lowbit(x) x&(-x)
#define ll long long
const int mod=1e9+7;
int a[10];
ll jc[105];
ll sum;
ll fast_mi(ll aa,ll bb){
ll res=1;
while(bb){
if(bb&1)res=res*aa%mod;
bb>>=1;
aa=aa*aa%mod;
}
return res;
}
int main(){
for(int i=0;i<=9;i++)cin>>a[i],sum+=a[i];
jc[0]=1;
for(int i=1;i<=sum;i++)jc[i]=jc[i-1]*i%mod;
sum=jc[sum];
for(int i=0;i<10;i++)
if(a[i])
sum=sum*fast_mi(jc[a[i]],mod-2)%mod;
cout<<sum<<endl;
return 0;
}

这个题有点不同 对于不同状态 有着不同的概率 所以我们要写dp方程
期望方程一般都是从后往前写
dp[i,j,k]表示当前有i枚金币 j枚银币 k枚铜币 满足题意的期望步数
dp[i,j,k]=p1×dp[i+1,j,k]+p2×dp[i,j+1,k]+p3×dp[i,j,k+1]+1
其中p1=i/i+j+k p2=j/i+j+k p3=k/i+j+k
点击查看代码
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 100;
double f[N + 1][N + 1][N + 1];
int main() {
for(int i = 99; i >= 0; i--) {
for(int j = 99; j >= 0; j--) {
for(int k = 99; k >= 0; k--) {
double pi = (double)i / (i + j + k);
double pj = (double)j / (i + j + k);
double pk = (double)k / (i + j + k);
f[i][j][k] = pi * f[i + 1][j][k] + pj * f[i][j + 1][k] + pk * f[i][j][k + 1] + 1;
}
}
}
int a, b, c;
cin >> a >> b >> c;
cout << fixed << setprecision(10) << f[a][b][c];
return 0;
}

这个题是属于相互独立的
设i为最大面值 考虑怎么才能保证一定取到i的方案数

点击查看代码
#include <bits/stdc++.h>
using namespace std;
double n,m;
double ans = 0;
int main()
{
cin >> m >> n;
double tmp = 0;
double last = 0;
for(int i = 1;i<=m;i++)
{
tmp = pow(i/m,n);
ans += (tmp-last)*i;
last = tmp;
}
cout.setf(ios_base::fixed,ios_base::fixed);
cout << setprecision(12) << ans << endl;
return 0;
}

期望倒着推

点击查看代码
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std ;
int R , C ;
double dw[1005][1005] , rg[1005][1005] , sy[1005][1005] ;
double mag[1005][1005] ;
int main(){
while( scanf( "%d%d" , &R , &C ) != EOF ){
for( int i = 1 ; i <= R ; i ++ )
for( int j = 1 ; j <= C ; j ++ )
scanf( "%lf%lf%lf" , &sy[i][j] , &rg[i][j] , &dw[i][j] ) ;
for( int i = 1 ; i <= R ; i ++ )
for( int j = 1 ; j <= C ; j ++ )
mag[i][j] = 10000000.0 ;
mag[R][C] = 0 ;
for( int i = R ; i ; i -- ){
for( int j = C ; j ; j -- ){
if( i == R && j == C ) continue ;
if( sy[i][j] == 1.00 ) continue ;
mag[i][j] = ( mag[i+1][j] * dw[i][j] + mag[i][j+1] * rg[i][j] + 2 ) / ( 1 - sy[i][j] ) ;
}
}
printf( "%.3f\n" , mag[1][1] ) ;
}
}

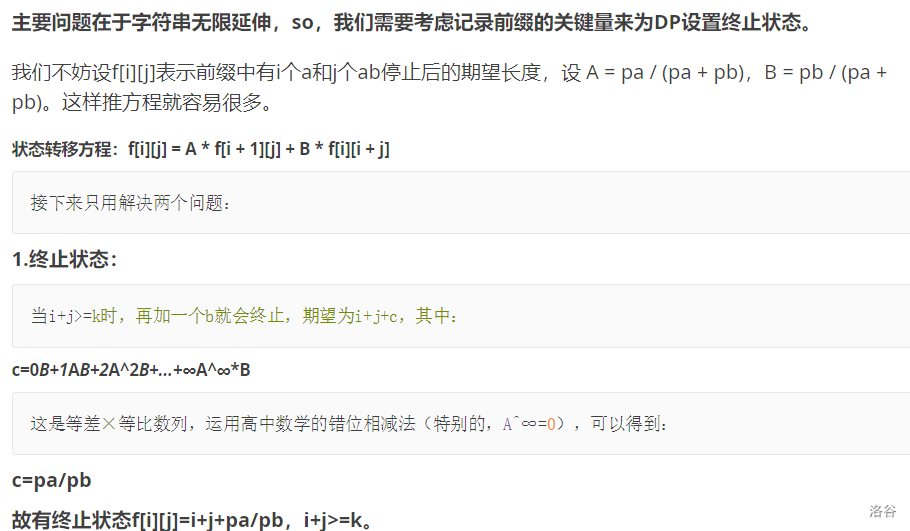
考虑初始状态dp[0,0] 可能最开始有无限个b 但是这对期望完全不会产生贡献 并且我们的式子会从他本身转移过来 所以设置dp[1,0]为初始状态
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define lowbit(x) x&(-x)
#define ll long long
const int mod=1e9+7;
const int maxn=1e3+5;
ll fast_mi(ll aa,ll bb){
ll res=1;
while(bb){
if(bb&1)res=res*aa%mod;
aa=aa*aa%mod;
bb>>=1;
}
return res;
}
ll dp[maxn][maxn];//dp[i,j]=pa*dp[i+1][j]+pb*dp[i][i+j]
ll k,pa,pb;
int main(){
cin>>k>>pa>>pb;
ll t=fast_mi(pa+pb,mod-2);
pa=pa*t%mod;
pb=pb*t%mod;
for(int i=k;i>=1;i--)
for(int j=k;j>=0;j--){
if(i+j>=k)
dp[i][j]=(i+j+pa*fast_mi(pb,mod-2)%mod)%mod;
else
dp[i][j]=(pa*dp[i+1][j]%mod+pb*dp[i][i+j]%mod)%mod;
}
cout<<dp[1][0]<<endl;
return 0;
}

这个题还有点偏博弈论

点击查看代码
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<queue>
#include<cstring>
#include<stack>
#define mod 998244353LL
#define mem(ss) memset(ss,0,sizeof(ss))
#define ll long long
#define io_opt ios::sync_with_stdio(false);cin.tie(0);cout.tie(0)
using namespace std;
ll gcd(ll a,ll b){return b==0?a:gcd(b,a%b);}
inline int read(){int data=0;char ch=0;while (ch<'0' || ch>'9') ch=getchar();while (ch>='0' && ch<='9') data=data*10+ch-'0',ch=getchar();return data;}
ll lowspeed(ll a,ll b,ll p){ll cur=a,ans=0;while(b){if(b&1) ans=(ans+cur)%p;cur=(cur+cur)%p;b>>=1;}return ans%p;}
ll speed(ll a,ll b,ll p){ll cur=a,ans=1;while(b){if(b&1) ans=lowspeed(ans,cur,p)%p;cur=lowspeed(cur,cur,p)%p;b>>=1;}return ans%p;}
ll T,A,B;
int main(){
io_opt;
cin>>T;
while(T--){
cin>>A>>B;
ll x=A+3*B;
ll y=4*(A+B);
ll gd=gcd(x,y);
cout<<x/gd<<'/'<<y/gd<<endl;
}
return 0;
}



对于期望我们一般考虑期望dp或者直接贡献,即要么利用期望的线性性,要么直接公式
而对于 pi 一般都是已知方案除以总方案。这题显然可以拆成三种贡献
- 已知数之间(树状数组处理)
2.未知数之间 (经典的逆序对问题) 考虑一对数 只可能是有顺序和逆序两种关系且两种概率相同 那么贡献就为sum*(sum-1)/4 其中sum为-1的总个数
3.已知和未知之间 枚举每个不为-1的数 设cnt1为比它大且供选择的数的个数 cnt2为比它小且可供选择的数的个数 它前面的-1的个数为res1 后面的-1的个数为res2
cnt1res1/sum +cnt2res2/sum
最后就是把所有的加起来
点击查看代码
#include<bits/stdc++.h>
#define lowb(x) (x&(-x))
using namespace std;
typedef long long ll;
const int maxn=2e5+5;
const ll mod=998244353;
int n,pi,c[maxn],a[maxn],pre[maxn],sum;
void add(int x,int val){
for(int i=x;i<=n;i+=lowb(i)){
c[i]+=val;
}
}
ll mypow(ll a,ll b){
ll ans=1;
while(b){
if(b&1)ans=ans*a%mod;
a=a*a%mod;
b>>=1;
}
return ans;
}
int ask(int x){
int ans=0;
for(int i=x;i;i-=lowb(i)){
ans+=c[i];
}
return ans;
}
int main(){
ll ans=0;
scanf("%d",&n);
for(int i=1;i<=n;++i)scanf("%d",&a[i]);
for(int i=1;i<=n;++i){
if(a[i]!=-1){
ans+=ask(n)-ask(a[i]);
add(a[i],1);
}else{
sum++;
}
pre[i]=pre[i-1]+(a[i]==-1);
if(ans>=mod)ans-=mod;
}
ll inv=mypow(sum,mod-2);
ll ans1=1ll*sum*(sum-1)%mod*mypow(4,mod-2)%mod;
ans=(ans+ans1)%mod;
for(int i=1;i<=n;++i){
if(a[i]!=-1){
int cnt=ask(n)-ask(a[i]);
ll x1=1ll*pre[i]*(n-a[i]-cnt)%mod*inv%mod;
int cnt2=ask(a[i]-1);
ll x2=1ll*(sum-pre[i])*(a[i]-1-cnt2)%mod*inv%mod;
ans=(ans+x1+x2)%mod;
}
}
cout<<ans<<"\n";
return 0;
}

对于重复独立实验 概率为p 期望为1/p
对于第一次 拿到第一个种类的概率为 n/n 期望为1
对于第二次 拿到第二个种类的概率为 n-1/n 期望为n/n-1
依次类推 最终答案为 n×(1/n +1/n-1 +1/n-2 +...+1/1)


首先 k个虫子互相独立 单独考虑一个虫子 最后答案就是k次方
设f[i] 表示一个虫子第i天全部死完的概率 因为虫子最多存活一天 所以我们考虑前一天有多少个新虫子生出来
有n种可能性 根据全概率公式

因为新生出来的虫子也是乘法原理 所以有次方
f(i)=p(0)+p(1)f(i-1)+p(2)(f(i-1)2)+...+p(n-1)*(f(n-1)(n-1))
实话说我真的理解不了为什么这样写 真的遇到了我也不可能写出来

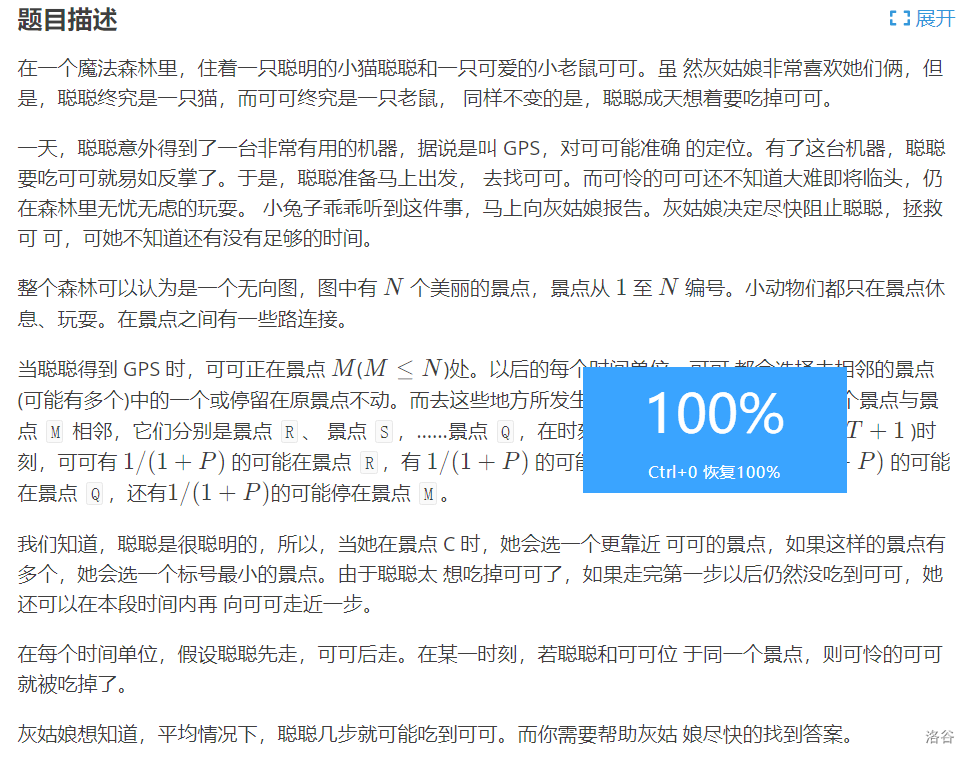
乍一看 好像绿豆蛙的归宿 区别就在于这个要删除一边 这样拓扑排序就不能用了
但是这个题只有600个点
考虑用dp 期望逆推

因为绿豆蛙的题目n太大了 所以不能用逆推

期望逆着推 设dp[i,j] 表示还剩i张红 j张黑的期望取值
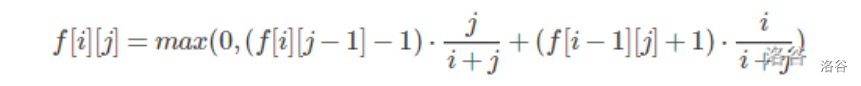
此时有人会有疑问 不是逆着推嘛 怎么是从i-1和j-1转移过来
正着推和逆着推不是这样看的 而是从设dp含义那里看 尽管是从i-1和j-1转移 但是任然是逆着推的

点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N=1005;
int n,m,l,r,v,a[N];
double dp[N][N<<1];
inline void cmax(double &x,double y) {
x=(x>y?x:y);
}
int main()
{
freopen("pigeon.in","r",stdin);
freopen("pigeon.out","w",stdout);
scanf("%d%d%d%d%d",&n,&m,&l,&r,&v),dp[n+1][m]=v;
for(int i=1; i<=n; ++i) scanf("%d",&a[i]);
for(int i=n; i>=1; i--)
{
double sum=0;
for(int j=l; j<=r; ++j) sum+=dp[i+1][min(j,m)]/(r-l+1);
for(int j=0; j<=m; ++j)
cmax(dp[i][j],dp[i+1][j]+a[i]),cmax(dp[i][j],sum),sum=sum-dp[i+1][min(j+l,m)]/(r-l+1)+dp[i+1][min(j+r+1,m)]/(r-l+1);
}
cout<<dp[1][0];
return 0;
}
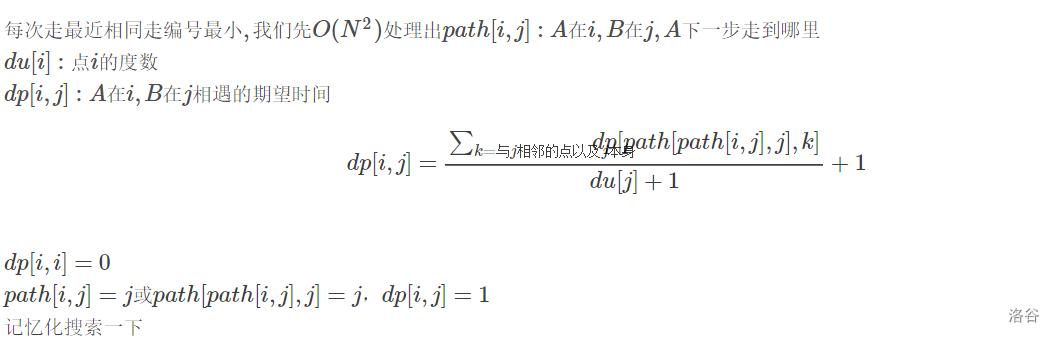
点击查看代码
#include<cstdio>
#include<queue>
#include<cstring>
#include<iostream>
using namespace std;
int cur,n,m,s,t;
int head[1005],p[1005];
int dis[1005][1005],nxt[1005][1005];
bool vis[1005],visit[1005][1005];
double f[1005][1005];
struct EDGE{
int t,next;
}e[2005];
#define INF 0x3f3f3f3f
void add(int a,int b)
{
cur++;
e[cur].t=b;
e[cur].next=head[a];
head[a]=cur;
}
queue < int > q;
void SPFA(int *dis,int *nxt,int s)
{
dis[s]=0;
q.push(s);
while (!q.empty())
{
int u=q.front();q.pop();
vis[u]=false;
for (int h=head[u];h!=-1;h=e[h].next)
{
int v=e[h].t;
if (dis[u]+1<dis[v])
{
dis[v]=dis[u]+1;
if (!vis[v])
{
vis[v]=true;
q.push(v);
}
}
}
}
}
double DFS(int u,int v)
{
if (visit[u][v]) return f[u][v];
if (u==v) return 0;
int fir=nxt[u][v];
int sec=nxt[fir][v];
if (fir==v||sec==v) return 1;
f[u][v]=1;
for (int h=head[v];h!=-1;h=e[h].next)
{
int w=e[h].t;
f[u][v]+=DFS(sec,w)/(p[v]+1);
}
f[u][v]+=DFS(sec,v)/(p[v]+1);
visit[u][v]=true;
return f[u][v];
}
int main()
{
scanf("%d%d%d%d",&n,&m,&s,&t);
memset(head,-1,sizeof head);
for (int i=1;i<=m;i++)
{
int a,b;
scanf("%d%d",&a,&b);
add(a,b);
add(b,a);
p[a]++;p[b]++;
}
for (int i=1;i<=n;i++)
{
for (int j=1;j<=n;j++)
dis[i][j]=nxt[i][j]=INF;
}
for (int i=1;i<=n;i++)
{
SPFA(dis[i],nxt[i],i);
}
for (int i=1;i<=n;i++)
for (int h=head[i];h!=-1;h=e[h].next)
{
int t=e[h].t;
for (int j=1;j<=n;j++)
if (dis[i][j]-1==dis[t][j])
{
nxt[i][j]=min(nxt[i][j],t);
}
}
printf("%.3lf",DFS(s,t));
return 0;
}

先预处理出每次游戏之后 两者所有相差的可能性 枚举前两次游戏相差分别为i j 第三次相差起码是i+j+1
所以再维护一个后缀就行 题目还是很简单的
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define lowbit(x) x&(-x)
#define ll long long
const int maxn=2e3+5;
const int maxm=5e3+5;
int n;
double tot,ans;
int a[maxn];
double dis[maxm],edd[maxm];
int main(){
cin>>n;tot=n*(n-1)/2;tot=tot*tot*tot;
for(int i=1;i<=n;i++)cin>>a[i];
sort(a+1,a+1+n);
for(int i=1;i<n;i++)
for(int j=i+1;j<=n;j++)
dis[a[j]-a[i]]++;
for(int i=maxm-2;i>=1;i--)edd[i]=edd[i+1]+dis[i];
for(int i=1;i<=maxm;i++)
for(int j=1;maxm-j-i>=1;j++)
ans+=(dis[i]*dis[j]*edd[i+j+1]/tot);
cout<<ans;
return 0;
}