
分析:
陷入Tarjan太深,浪费了很多无用的时间
很明显如果是一棵树的话,直接都染黑了
然后就想到要将每一个连通块都变为一棵树
设连通块总数为C,总共有m条边,有用的就只有n-C条
所以要染色的就有m-n+C直接并查集维护
总结:当时真的是脑残,去找环了

分析:
首先答案是很多个数中找一个,二分一个答案M
问题转化为求 [1,M] 内有多少个数字在至少一个S(ni) 里面。
如果是可重复的话,直接计算有多少个数在S里面就好
但是不可重复的当然就要考虑容斥
补充:容斥原理

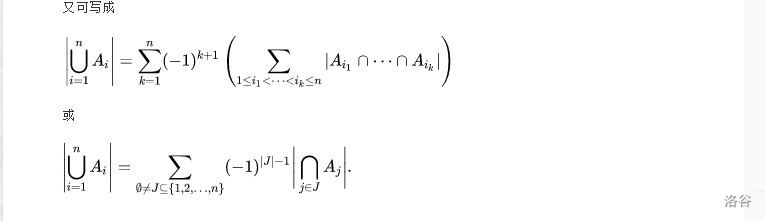
我们考虑先计算出有多少个 [1,M] 中的数在 S(n1),S(n2),··· ,S(nk) 中,
然后把它们都加起来。 显然这样算多了:
如果某个数字同时在多个 S(ni) 里面,那么他就重复了。
于是 我们考虑再去掉在至少两个 S(ni) 中的,
然后加上至少三个 S(ni) 中的,
去掉至少四 个 S(ni) 中的……
再考虑一个数如果既是2的次幂,又是3的次幂,那么它也一定是lcm(2,3)=6的次幂

code by chitongzi:
#include <bits/stdc++.h>
#define xx first
#define yy second
#define ll long long
#define mp make_pair
#define pb push_back
#define debug(...) fprintf(stderr,__VA_ARGS__)
#define int long long
using namespace std;
inline long long fpow (long long base, long long v)
{
long long tot = 1;
while (v)
{
if (v & 1) {
if (1000000000000000000LL / base < tot) return 1LL << 60;
tot *= base;
}
base *= base;
v >>= 1;
if (!base) return v ? 1LL << 60 : tot;
if (v > 1 && tot > 1000000000LL) return (1LL << 60);
}
return tot;
}
inline int gcd (int u, int v)
{
return !v ? u : gcd (v, u % v);
}
const int N = 65;
int g[N][N], n, m, a[N];
long long dp[N][N];
inline long long check (long long k)
{
long long res = 0;
for (int i = 1; i <= 60; ++i)
{
if (!dp[n][i]) continue;
long long p = pow (k, 1.0 / i);
while (fpow (p, i) > k) p--;
while (fpow (p + 1, i) <= k) p++;
p--;//here
res += dp[n][i] * p;
}
return res + 1;
}
signed main ()
{
for (int i = 1; i <= 60; ++i)
for (int j = 1; j <= 60; ++j)
g[i][j] = i * j / gcd (i, j);
int q;
scanf ("%lld", &q);
while (q--)
{
scanf ("%lld%lld", &m, &n);
for (int i = 1; i <= n; ++i)
scanf ("%lld", &a[i]);
memset (dp, 0, sizeof dp);
dp[0][0] = -1;
for (int i = 0; i < n; ++i)
{
for (int j = 0; j <= 60; ++j)
{
if (!dp[i][j]) continue;
dp[i + 1][j] += dp[i][j];
int lcm = j ? j / gcd (j, a[i + 1]) * a[i + 1] : a[i + 1];
if (lcm > 60) continue;
dp[i + 1][lcm] -= dp[i][j];
}
}
// for (int i = 0; i <= n; ++i, puts (""))
// for (int j = 0; j <= 20; ++j)
// printf ("%lld ", dp[i][j]);
long long l = 1, r = 100000000000000000LL, mid;
while (l < r)
{
mid = (l + r) / 2;
if (check (mid) < m) l = mid + 1;
else r = mid;
}
printf ("%lld
", l);
}
return 0;
}

按位与
我们按照从高位到低位的顺序进行贪心,
如果当前位有至少两个数字是 1,那么 我们可以让这一位是 1,
因此最终答案的这一位一定是 1。
所 以我们可以去掉所有这一位为 0 的数字,然后继续向下贪心即可。
最后的方案数就是 剩余的数字中选出两个的方案数。
按位异或
这样就是01trie树的经典例题,但貌似我打卦了
按位或
同样地在确定了一个数之后从高到低贪心。
但是这里又多了一个问题:如果这个 数字的当前位是 1,那么我们仍然没法减少候选范围
然后就是什么高维前缀和乱搞
高维前缀和题外话:
求子集和
for(int j=0;j<n;j++)
for(int i=0;i<1<<n;i++)
if(i&(1<<j)) dp[i]+=dp[i^(1<<j)];
求超集和