题目地址:https://leetcode-cn.com/problems/yuan-quan-zhong-zui-hou-sheng-xia-de-shu-zi-lcof/
题目描述
0,1,,n-1这n个数字排成一个圆圈,从数字0开始,每次从这个圆圈里删除第m个数字。求出这个圆圈里剩下的最后一个数字。
例如,0、1、2、3、4这5个数字组成一个圆圈,从数字0开始每次删除第3个数字,则删除的前4个数字依次是2、0、4、1,因此最后剩下的数字是3。
题目示例
示例 1:
输入: n = 5, m = 3
输出: 3
示例 2:
输入: n = 10, m = 17
输出: 2
解题思路
递归:此问题可以理解为约瑟夫问题,即n个人围成一圈,第一个人从1开始报数,报m的将被杀掉,下一个人接着从1开始报。如此反复,最后剩下一个,即为此轮胜利者,如此求最后的胜利者。使用递归的方式解决,递归公式如下,具体的推导流程可参考文末文章,思路很清晰。
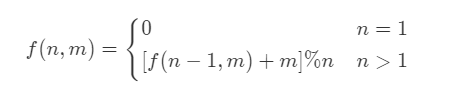
迭代:此方法是在递归方法基础上进行修改,我们知道最终胜利的人是只有一个人的时候,此时她的下标index=0,继续分析,当有两个人的时候,胜利者的下标index=1,如此往复下去,可总结出迭代规律,具体见下面:
此处,我们取n=5,m=3。其中,f(n,m)为最终胜利者下标索引值。
0、1、2、3、4这5个数字组成一个圆圈,从数字0开始每次删除第3个数字,则删除的前4个数字依次是2、0、4、1,因此最后剩下的数字是3,即胜利者下标为3.
当人数n=1时,胜利者下标f(1,3)=0;
当人数n=2时,胜利者下标f(2,3)=(0+3)%2=1
当人数n=3时,胜利者下标f(3,3)=(1+3)%3=1
当人数n=4时,胜利者下标f(4,3)=(1+3)%4=0
当人数n=5时,胜利者下标f(5,3)=(0+3)%5=3
以此推广下去,可以总结得
n=1时,f(1,3)=0;
n=2时,f(2,3)=(f(1,3)+3)%3=1
n=3时,f(3,3)=((f(1,3)+3)%3+3)%3=1
n=4时,f(4,3)=(((f(1,3)+3)%3+3)%3+3)%4
n=5时,f(5,3)=((((f(1,3)+3)%3+3)%3+3)%4+3)%5
........
n=N时,f(N,M)=(f(N-1,M)%N;
程序源码
递归
class Solution { public: int lastRemaining(int n, int m) { if(n == 1) return 0; //若剩下一个人,必然是胜利者 else return (m + lastRemaining(n - 1, m)) % n; } };
迭代
class Solution { public: int lastRemaining(int n, int m) { int winIndex = 0; for(int i = 2; i <= n; i++) { winIndex = (winIndex + m) % i; } return winIndex; } };
参考文章