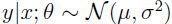
在分类问题中我们如果：
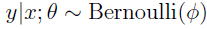
他们都是广义线性模型中的一个样例，在理解广义线性模型之前须要先理解指数分布族。
指数分布族（The Exponential Family）
假设一个分布能够用例如以下公式表达，那么这个分布就属于指数分布族：
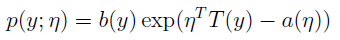
公式中y是随机变量；h(x)称为基础度量值（base measure）；
η称为分布的自然參数（natural parameter），也称为标准參数（canonical parameter）；
T(y)称为充分统计量，通常T(y)=y；
a(η)称为对数切割函数（log partition function）；
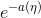本质上是一个归一化常数。确保
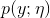概率和为1。
当T(y)被固定时，a(η)、b(y)就定义了一个以η为參数的一个指数分布。我们变化η就得到这个分布的不同分布。
伯努利分布属于指数分布族。伯努利分布均值为φ，写为Bernoulli(φ)。是一个二值分布，y ∈ {0, 1}。所以p(y = 1; φ) = φ; p(y = 0; φ) = 1 − φ。当我们变化φ就得到了不同均值的伯努利分布。伯努利分布表达式转化为指数分布族表达式步骤例如以下：
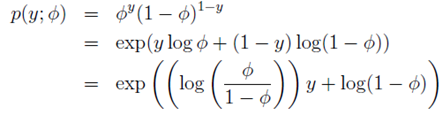
当中，
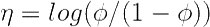
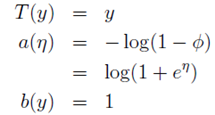
再举一个高斯分布的样例。高斯分布也属于指数分布族。由高斯分布能够推导出线性模型（推导过程将在EM算法中解说）。由星型模型的如果函数能够得知，高斯分布的方差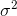
与如果函数无关，因而为了计算简便，我们设方差
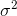=1。
高斯分布转化为指数分布族形式的推导步骤例如以下：
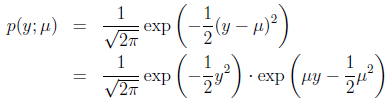
当中
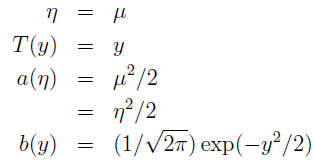
更多分部也属于指数分布族。比如：伯努利分布（Bernoulli）、高斯分布（Gaussian）、多项式分布（Multinomial）、泊松分布（Poisson）、伽马分布（Gamma）、指数分布（Exponential）、β分布、Dirichlet分布、Wishart分布。
构建广义线性模型（Constructing GLMs）
在分类和回归问题中，我们通过构建一个关于x的模型来预測y。这样的问题能够利用广义线性模型（Generalized linear models，GMLs）来解决。构建广义线性模型我们基于三个如果。也能够理解为我们基于三个设计决策。这三个决策帮助我们构建广义线性模型：
-
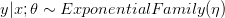,如果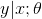
满足一个以为參数的指数分布。比如，给定了输入x和參数θ。那么能够构建y关于的表达式。 -
给定x。我们的目标是要确定T(y)。即
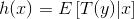。大多数情况下T(y)=y，那么我们实际上要确定的是
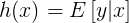。即给定x，如果我们的目标函数是
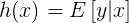。（在逻辑回归中期望值是。因此目标函数h是φ。在线性回归中期望值是μ，而高斯分布中
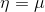，因此线性回归中目标函数
）。 -
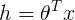如果自然參数η和x是线性相关，即如果：
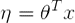
如果有一个预測问题：基于特征商店促销活动、近期的广告、天气、星期几等特征x。来预測商店在任一小时内的顾客数目y。
依据概率知识可知，x、y符合泊松分布。泊松分布属于指数分布族。我们能够利用上面的3个如果。构建一个广义线性模型来进行构建预測模型。
GLMs构建最小二模型
线性回归中的优化目标y（损失函数）是由最小二乘法得到的。能够使用广义线性模型构建最小二乘模型。三个如果：
-
最小二乘法得到的目标变量y是一个连续值，我们如果给定x下y的分布符合高斯分布。
如果1中的ExponentialFamily(η)就是高斯分布。
-
在高斯分布中
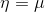。目标函数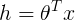
-
如果：
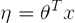
推导步骤例如以下：
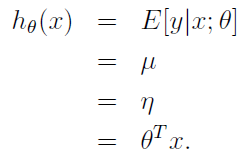
第一步变换依据如果2：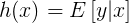
第二步变换依据y|x; θ ∼ N(μ, σ2)，高斯分布的期望值是μ
第三步依据如果1：高斯分布中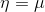
第四步依据如果3：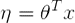
如今已经使用广义线性模型构建出了最小二乘模型。接下来的工作就是利用梯度下降、牛顿方法来求解θ。梯度下降、牛顿方法的内容请參考之前的讲义。
GLMs构建逻辑回归
逻辑回归能够用于解决二分类问题，而分类问题目标函数y是二值的离散值，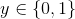
。依据统计知识。二分类问题能够选择伯努利分布来构建模型。
在伯努利分布的指数分布族表达式中我们已知：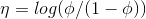
，从而得到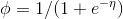
。
构建广义线性模型的三个如果：
-
如果符合伯努利分布，
-
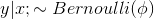
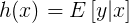。伯努利分布中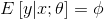
-
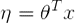
推导步骤例如以下：
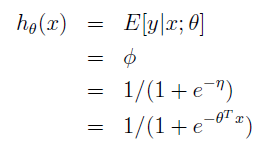
同最小二乘模型一样。接下来的工作就由梯度下降或牛顿方法来完毕。
注意一下上面的推到结果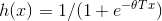
，回顾一下，在逻辑回归中。我们选用Sigmoid函数
。
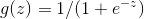之所以在逻辑回归中选用这个g(z)作为Sigmoid函数是由一套理论作支持的。这个理论便是广义线性模型。