题目传送门(内部题151)
输入格式
第一行一个整数$N$。
第二行$N$个整数,第$i$个为$a_i$。
输出格式
一行一个整数,表示答案。为避免精度误差,答案对$323232323$取模。
即设答案化为最简分式后的形式为$frac{a}{b}$,其中$a$和$b$互质。输出整数$x$使得$bxequiv a(mod 323232323)$且$0leqslant x<323232323$。可以证明这样的整数$x$是唯一的。
样例
样例输入:
3
2 3 3
样例输出:
202020207
数据范围与提示
每个测试点$10$分,共$10$个测试点:
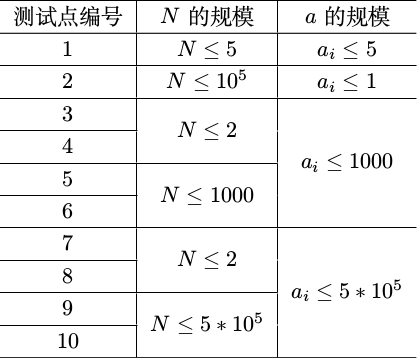
对于所有的数据,有:$1leqslant N,a_i$。
题解
考虑$DP$,设$f_i$表示$a_i$被选的期望次数,注意这里是$a_i$。
那么答案就是:
$$ans=sumlimits_{i=2}^nf_{a_i}}+a_1$$
想办法求出$f_i$。
考虑从$Nleqslant 2$入手,相当于是从$(a_1,a_i)$走到坐标轴的期望次数,每次都有$frac{1}{2}$的概率走不同的方向;类比这种做法,可以列出$a_i$的贡献式子:
$$sumlimits_{i=0}^{a_i-1}i imes frac{C_{a_1-1+i}^i}{2^{a_1+i}}+a_i imes (1-sumlimits_{i=0}^{a_i-1}frac{C_{a_1-1+i}^i}{2^{a_1+i}}$$
看似还是$Theta(N^2)$的,但是实际上我们可以线性递推出来$f[i]$,然后直接统计答案就好了。
时间复杂度:$Theta(max(a_i))$。
期望得分:$100$分。
实际得分:$100$分。
代码时刻
#include<bits/stdc++.h>
using namespace std;
const int mod=323232323;
const int in2=161616162;
int N;
int a[500001];
long long fac[500001],inv[500001];
long long f[500001],w,p,inc,res;
long long ans;
long long qpow(long long x,long long y)
{
long long res=1;
while(y)
{
if(y&1)res=res*x%mod;
x=x*x%mod;y>>=1;
}
return res;
}
void pre_work()
{
fac[0]=1;
for(int i=1;i<=500000;i++)fac[i]=fac[i-1]*i%mod;
inv[500000]=qpow(fac[500000],mod-2);
for(int i=500000;i;i--)inv[i-1]=inv[i]*i%mod;
}
long long C(int x,int y){return fac[x]*inv[y]%mod*inv[x-y]%mod;}
int main()
{
pre_work();
scanf("%d",&N);
for(int i=1;i<=N;i++)
scanf("%d",&a[i]);
inc=p=qpow(qpow(2,a[1]),mod-2);
for(int i=1;i<=500000;i++)
{
inc=inc*in2%mod;
f[i]=(w+i*(1-p)+mod)%mod;
res=C(a[1]-1+i,i)*inc%mod;
p=(p+res)%mod;w=(w+res*i)%mod;
}
ans=a[1];
for(int i=2;i<=N;i++)ans=(ans+f[a[i]]+mod)%mod;
printf("%lld",ans);
return 0;
}
rp++