题目传送门(内部题113)
输入格式
第一行一个正整数$n$。
接下来$n$行,每行$n$个整数,描述$C$矩阵。保证输入的是一个林先森矩阵。
输出格式
若不可能实现,则输出一行$Impossible$;否则,输出一行一个仅包含${U,D,L,R}$的字符串,表示一个$typ$参数的序列。你的序列长度不能超过$10^6$。若不需要进行任何操作,请将该序列留空。
样例
样例输入1:
2
1 2
3 0
样例输出1:
Impossible
样例输入2:
3
3 2 5
4 1 8
6 7 0
样例输出2:
UULDLU
数据范围与提示
本题采用子任务评分。仅当你通过一个子任务下所有测试点时,你才能获得该子任务的分数。
对于所有数据,$1leqslant nleqslant 50$。
$1.$($30$分)$nleqslant 3$。
$2.$($30$分)$nleqslant 10$。
$3.$($40$分)没有特殊限制。
题解
其实就是一个大模拟。
我们考虑从小到大填,也就是先填好右下角,每一行从右到左填,从下到上依次填好每一行,直到最后两行不管。
先说怎么填好每一行。
首先,先填好每一行$3sim n$的每一个数,方法很简单,不再赘述。
$1,2$位置需要一起填,具体方法我们可以先想办法将其变成如下图所示的情况$downarrow$

上图中,黑色为已经填好的块和边界,橙色为准备填的两个块,这样我们只需要将$0$向左再向上移动即可移动成下图的状态$downarrow$
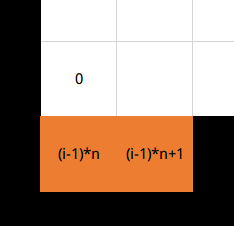
剩余$1,2$两行没有填好时只需要按上面填每行的$1,2$的方法填补即可。
最后剩下左上角一个$2 imes 2$的方格时判断即可。
时间复杂度:$Theta(n^3)$。
期望得分:$100$分。
实际得分:$100$分。
代码时刻
#include<bits/stdc++.h>
using namespace std;
int n;
int Map[55][55],sec[55][55];
bool vis[55][55];
pair<int,int> pos[10000];
int top;
char ans[10000010];
int dis(int x,int y,int x2,int y2){return abs(x-x2)+abs(y-y2);}
void U()
{
swap(Map[pos[0].first][pos[0].second],Map[pos[0].first-1][pos[0].second]);
swap(pos[0],pos[Map[pos[0].first][pos[0].second]]);ans[++top]='U';
if(top>1e6){puts("Impossible");exit(0);}
}
void D()
{
swap(Map[pos[0].first][pos[0].second],Map[pos[0].first+1][pos[0].second]);
swap(pos[0],pos[Map[pos[0].first][pos[0].second]]);ans[++top]='D';
if(top>1e6){puts("Impossible");exit(0);}
}
void L()
{
swap(Map[pos[0].first][pos[0].second],Map[pos[0].first][pos[0].second-1]);
swap(pos[0],pos[Map[pos[0].first][pos[0].second]]);ans[++top]='L';
if(top>1e6){puts("Impossible");exit(0);}
}
void R()
{
swap(Map[pos[0].first][pos[0].second],Map[pos[0].first][pos[0].second+1]);
swap(pos[0],pos[Map[pos[0].first][pos[0].second]]);ans[++top]='R';
if(top>1e6){puts("Impossible");exit(0);}
}
int judge(int x,int y)
{
if(pos[0]==make_pair(x,y+1))return 1;
if(pos[0]==make_pair(x,y-1))return 2;
if(pos[0]==make_pair(x-1,y))return 3;
if(pos[0]==make_pair(x+1,y))return 4;
return 0;
}
void change(int x,int y)
{
while(1)
{
if(judge(x,y))break;
int flag=0;
if(pos[0].first-1==x&&pos[0].second==y)goto nxt1;
if(pos[0].first>1&&dis(x,y,pos[0].first,pos[0].second)>dis(x,y,pos[0].first-1,pos[0].second)&&!vis[pos[0].first-1][pos[0].second]){U();flag=1;}
nxt1:;
if(pos[0].first+1==x&&pos[0].second==y)goto nxt2;
if(pos[0].first<n&&dis(x,y,pos[0].first,pos[0].second)>dis(x,y,pos[0].first+1,pos[0].second)&&!vis[pos[0].first+1][pos[0].second]){D();flag=1;}
nxt2:;
if(pos[0].first==x&&pos[0].second-1==y)goto nxt3;
if(pos[0].second>1&&dis(x,y,pos[0].first,pos[0].second)>dis(x,y,pos[0].first,pos[0].second-1)&&!vis[pos[0].first][pos[0].second-1]){L();flag=1;}
nxt3:;
if(pos[0].first==x&&pos[0].second+1==y)goto nxt4;
if(pos[0].second<n&&dis(x,y,pos[0].first,pos[0].second)>dis(x,y,pos[0].first,pos[0].second+1)&&!vis[pos[0].first][pos[0].second+1]){R();flag=1;}
nxt4:;
if(!flag)break;
}
}
void move(int k,int x,int y)
{
int opt=judge(x,y);
switch(k)
{
case 1:
if(opt==1){U();L();D();}
if(opt==2){U();R();D();}
if(opt==3)D();
if(opt==4)
{
if(y>1){L();U();U();R();D();}
else{R();U();U();L();D();}
}
break;
case 2:
if(opt==1)
{
if(vis[x+1][y+1]){U();L();D();D();R();U();L();U();R();D();D();L();U();}
else{D();L();U();}
}
if(opt==2){D();R();U();}
if(opt==3)
{
if(y<n){R();D();}
else{L();D();D();R();U();}
}
if(opt==4)U();
break;
case 3:
if(opt==1){U();L();L();D();R();}
if(opt==2)R();
if(opt==3){L();D();R();}
if(opt==4){L();U();R();}
break;
case 4:
if(opt==1)L();
if(opt==2)
{
if(x>1){U();R();R();D();L();}
else
{
if(vis[x+1][y+1]){R();D();R();U();L();D();R();U();L();L();D();R();R();U();L();}
else{D();R();R();U();L();}
}
}
if(opt==3){R();D();L();}
if(opt==4)
{
if(vis[x+1][y+1]){L();U();}
else{R();U();L();}
}
break;
}
}
void move(int x,int y)
{
int res=sec[x][y];
while(pos[res]!=make_pair(x,y))
{
bool flag=0;
if(pos[res].first>1&&dis(x,y,pos[res].first,pos[res].second)>dis(x,y,pos[res].first-1,pos[res].second)&&!vis[pos[res].first-1][pos[res].second])
{change(pos[res].first,pos[res].second);move(1,pos[res].first,pos[res].second);flag=1;}
if(pos[res].first<n&&dis(x,y,pos[res].first,pos[res].second)>dis(x,y,pos[res].first+1,pos[res].second)&&!vis[pos[res].first+1][pos[res].second])
{change(pos[res].first,pos[res].second);move(2,pos[res].first,pos[res].second);flag=1;}
if(pos[res].second>1&&dis(x,y,pos[res].first,pos[res].second)>dis(x,y,pos[res].first,pos[res].second-1)&&!vis[pos[res].first][pos[res].second-1])
{change(pos[res].first,pos[res].second);move(3,pos[res].first,pos[res].second);flag=1;}
if(pos[res].second<n&&dis(x,y,pos[res].first,pos[res].second)>dis(x,y,pos[res].first,pos[res].second+1)&&!vis[pos[res].first][pos[res].second+1])
{change(pos[res].first,pos[res].second);move(4,pos[res].first,pos[res].second);flag=1;}
if(!flag)break;
}
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
{
scanf("%d",&Map[i][j]);sec[i][j]=(i-1)*n+j-1;
pos[Map[i][j]]=make_pair(i,j);
}
for(int i=n;i>2;i--)
for(int j=n;j;j--)
{
move(i,j);
vis[i][j]=1;
}
for(int j=n;j>1;j--)
{
move(2,j);vis[2][j]=1;
move(1,j);vis[1][j]=1;
}
if(pos[0]!=make_pair(1,1)){swap(Map[1][1],Map[2][1]);ans[++top]='U';}
printf("%s",ans+1);
return 0;
}
rp++