题目传送门(内部题65)
输入格式
第一行,一个自然数$T$,代表数据组数。
对于每组数据:
第一行,一个正整数$n$,一个自然数$m$。
接下来$n$行,每行两个正整数,$a_i,b_i$。
输出格式
对于每组数据,输出一行,一个整数,代表答案。
样例
样例输入:
3
2 0
5 10
5 5
2 1
1 1
2 2
3 1
3 5
4 4
5 3
样例输出:
25
4
12
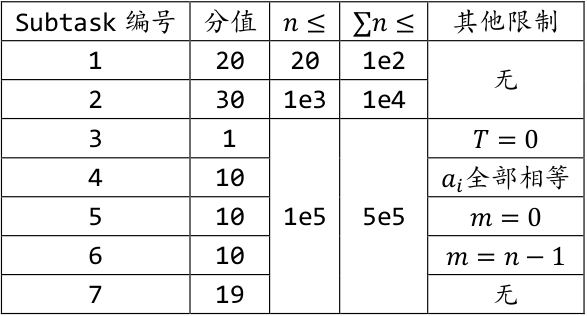
数据范围与提示
保证$0leqslant m<n,a_i,b_ileqslant 10^5$。
题解
题目并不难,考虑贪心,显然把$m$都用完一定不劣。
先将所有矩形按照$a_i$为第一维$b_i$为第二维排序,先将最后$m$个删去,将$b_i$加入树状数组,然后往前扫,不断改变策略,更新答案就好了。
时间复杂度:$Theta(sum nlog sum n)$。
期望得分:$100$分。
实际得分:$100$分。
代码时刻
#include<bits/stdc++.h>
using namespace std;
struct rec{int a,b;}e[100001];
int n,m;
int minb,maxb;
bool vis[100001];
int tr[100001];
long long ans;
bool cmp(rec a,rec b){return a.a==b.a?a.b<b.b:a.a<b.a;}
void pre_work()
{
memset(tr,0,sizeof(tr));
memset(vis,0,sizeof(vis));
minb=0x3f3f3f3f;ans=maxb=0;
}
int lowbit(int x){return x&-x;}
void add(int x)
{
for(int i=x;i<=maxb;i+=lowbit(i))
tr[i]++;
}
int ask(int x)
{
int res=0;
for(int i=x;i;i-=lowbit(i))res+=tr[i];
return res;
}
int main()
{
int T;scanf("%d",&T);
if(!T)return 0;
while(T--)
{
pre_work();
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
{
scanf("%d%d",&e[i].a,&e[i].b);
vis[e[i].b]=1;maxb=max(maxb,e[i].b);
}
sort(e+1,e+n+1,cmp);
for(int i=n;i>m+1;i--)
{
add(e[i].b);
minb=min(minb,e[i].b);
}
minb=min(minb,e[m+1].b);
for(int i=m+1;i;i--)
{
add(e[i].b);
if(e[i].a==e[i-1].a)continue;
while(ask(minb)<m-i+2)minb++;
while(!vis[minb])minb++;
ans=max(ans,1LL*e[i].a*minb);
}
printf("%lld
",ans);
}
return 0;
}
rp++