题目背景
$frac{1}{4}$遇到了一道水题,$eooooo$完全不会做,于是去请教小$D$。结果小$D$已经去了阿塞拜疆,于是,$frac{1}{4}$只好来问你,这道题是这样的:
题目描述
在数轴上有一个线段,左端点在$0$,长度为$l$。
现在需要按顺序完成$n$个任务,第$i$个任务可以用$x_i$表示:当线段接触到点$x_i$时,视为完成任务,也就是$x_i$在线段某一端点上、或两端点之间。
你可以任意平移线段,求依次完成任务所需要的最短的平移总距离。
$q$次询问,每次给出一个$l$。
输入格式
从文件$z.in$中读入数据。
第一行,两个自然数$n,q$。
第二行,$n$个整数代表$x_i$。
第三行,$q$个自然数,代表询问的$l$。
输出格式
输出到文件$z.out$中。
输出$q$行,每行一个整数,代表对应询问的答案。
样例
样例输入1:
9 6
2 -3 -1 1 2 3 5 3 7
0 1 2 3 4 5
样例输出1:
21
16
11
10
9
8
样例输入2:
8 8
5 0 5 15 0 -10 0 -20
20 15 14 11 10 5 1 0
样例输出2:
20
20
22
28
30
50
74
80
数据范围与提示
样例$1$解释:
当$l=3$时:
一开始在$[0,3]$,完成任务$1$。
移动到$[−3,0]$,完成任务$2,3$。
移动到$[0,3]$,完成任务$4,5,6$。
移动到$[2,5]$,完成任务$7,8$。
移动到$[4,7]$,完成任务$9$。
$ans=3+3+2+2=10$。
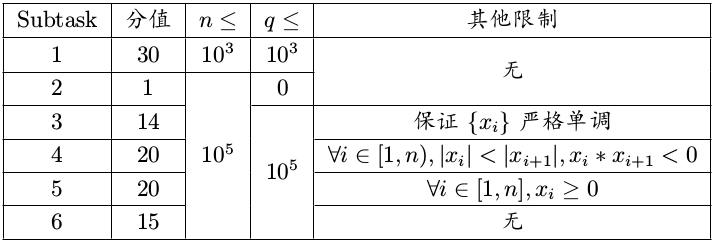
数据范围:
保证$n,qin [0,10^5],x_iin [−10^9,10^9],lin [0,10^9]$。
题解
首先,必须是挨个完成任务,所以如果有一个任务满足$x_{i-1}<x_i<x_{i+1}$或$x_{i-1}>x_i>x_{i+1}$,那么可以删去它。
这样的话,路径肯定是向前走再向后走,于是我们先假设$l=0$,那么答案会是一个一次函数。
那么接着考虑$l eq 0$,如果$l$不超过最小的位移绝对值时,答案还是一个一次函数;如果超过了的话,我们可以将三个位移合并为一个即可。
将问题离线,利用$map$和$prority_queue$维护即可最小绝对值即可。
代码实现稍复杂u,调了好久……
时间复杂度:$Theta(nlog n)$。
期望得分:$100$分。
实际得分:$100$分。
代码时刻
#include<bits/stdc++.h>
using namespace std;
int N,Q;
int x[100001];
pair<int,int> l[100001];
map<int,int> mp;
long long sum,ans[100001];
priority_queue<pair<int,int>,vector<pair<int,int> >,greater<pair<int,int> > > q;
long long calc(long long x)
{
if(!mp.empty()&&mp.begin()->second<0)return sum-(mp.size()-1)*x;
return sum-mp.size()*x;
}
int main()
{
scanf("%d%d",&N,&Q);
int lst=0;
for(int i=1;i<=N;i++)
{
int a;scanf("%d",&a);
if(a==lst)continue;
if(x[0]&&((x[x[0]]<0&&a<lst)||(x[x[0]]>0&&a>lst)))x[x[0]]+=a-lst;
else x[++x[0]]=a-lst;
lst=a;
}
for(int i=1;i<=Q;i++)
{
scanf("%d",&l[i].first);
l[i].second=i;
}
sort(l+1,l+Q+1);
for(int i=1;i<=x[0];i++)
{
sum+=abs(x[i]);
mp[i]=x[i];
q.push(make_pair(abs(x[i]),i));
}
int t=1;
while(!q.empty())
{
pair<int,int> flag=q.top();q.pop();
auto _=mp.lower_bound(flag.second);
pair<int,int> p=make_pair(_->first,_->second);
if(_==mp.end()||p.first!=flag.second||abs(p.second)!=flag.first)continue;
while(t<=Q&&abs(p.second)>l[t].first)ans[l[t].second]=calc(l[t++].first);
auto begin=mp.begin();
if(p!=make_pair(begin->first,begin->second))
{
auto endle=prev(mp.end());
if(p!=make_pair(endle->first,endle->second))
{
auto pr=prev(_),nx=next(_);
mp.erase(pr);mp.erase(nx);
pair<int,int> pre=make_pair(pr->first,pr->second);
pair<int,int> nxt=make_pair(nx->first,nx->second);
flag.first=p.second;
sum-=abs(p.second);
flag.first+=pre.second;
sum-=abs(pre.second);
flag.first+=nxt.second;
sum-=abs(nxt.second);
_->second=flag.first;
sum+=abs(flag.first);
q.push(make_pair(abs(flag.first),flag.second));
}
else
{
sum-=abs(p.second);
mp.erase(_);
}
}
else
{
if(p.second>0)
{
auto endle=prev(mp.end());
if(p!=make_pair(endle->first,endle->second))
{
auto nx=next(_);mp.erase(nx);
pair<int,int> nxt=make_pair(nx->first,nx->second);
flag.first=p.second;
sum-=abs(p.second);
flag.first+=nxt.second;
sum-=abs(nxt.second);
if(flag.first)
{
_->second=flag.first;
sum+=abs(flag.first);
q.push(make_pair(abs(flag.first),flag.second));
}
else mp.erase(_);
}
else
{
sum-=abs(p.second);
mp.erase(_);
}
}
}
}
while(t<=Q)ans[l[t].second]=calc(l[t++].first);
for(int i=1;i<=Q;i++)printf("%lld
",ans[i]);
return 0;
}
rp++