数据的偏度和峰度——df.skew()、df.kurt()

我们一般会拿偏度和峰度来看数据的分布形态，而且一般会跟正态分布做比较，我们把正态分布的偏度和峰度都看做零。如果我们在实操中，算到偏度峰度不为0，即表明变量存在左偏右偏，或者是高顶平顶这么一说。

一.偏度（Skewness）

Definition:是描述数据分布形态的统计量，其描述的是某总体取值分布的对称性，简单来说就是数据的不对称程度。。
偏度是三阶中心距计算出来的。
（1）Skewness = 0 ，分布形态与正态分布偏度相同。
（2）Skewness > 0 ，正偏差数值较大，为正偏或右偏。长尾巴拖在右边，数据右端有较多的极端值。
（3）Skewness < 0 ，负偏差数值较大，为负偏或左偏。长尾巴拖在左边，数据左端有较多的极端值。
（4）数值的绝对值越大，表明数据分布越不对称，偏斜程度大。
计算公式：
Skewness=E[((x-E(x))/(sqrt{D(x)}))^3]
| Skewness| 越大，分布形态偏移程度越大。

二.峰度（Kurtosis）

Definition:偏度是描述某变量所有取值分布形态陡缓程度的统计量，简单来说就是数据分布顶的尖锐程度。
峰度是四阶标准矩计算出来的。
（1）Kurtosis=0 与正态分布的陡缓程度相同。
（2）Kurtosis>0 比正态分布的高峰更加陡峭——尖顶峰
（3）Kurtosis<0 比正态分布的高峰来得平台——平顶峰
计算公式：
Kurtosis=E[ ( (x-E(x))/ (sqrt(D(x))) )^4 ]-3

参考：https://support.minitab.com/zh-cn/minitab/18/help-and-how-to/statistics/basic-statistics/supporting-topics/data-concepts/how-skewness-and-kurtosis-affect-your-distribution/

三.举栗子，用强大的Pandas来计算偏度和峰度：

import pandas as pd
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns
iris = load_iris()
x = iris.data
y = iris.target

xx = pd.DataFrame(x,columns=iris.feature_names)

sns.pairplot(xx)

<seaborn.axisgrid.PairGrid at 0x957051a5f8>

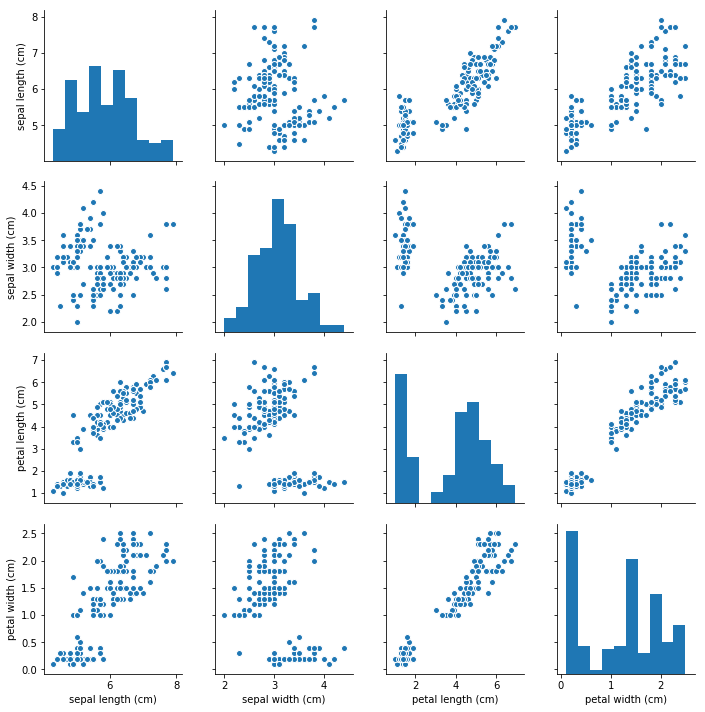
print("鸢尾花四个变量的偏度：
", xx.skew())
print("====="*7)
print("鸢尾花四个变量的峰度：
", xx.kurt())

鸢尾花四个变量的偏度：
 sepal length (cm)    0.314911
sepal width (cm)     0.334053
petal length (cm)   -0.274464
petal width (cm)    -0.104997
dtype: float64
===================================
鸢尾花四个变量的峰度：
 sepal length (cm)   -0.552064
sepal width (cm)     0.290781
petal length (cm)   -1.401921
petal width (cm)    -1.339754
dtype: float64